
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 54. Тема 3 : Тройной интеграл
|
|
|
|
3.1. Определение и вычисление тройного интеграла
Исходя из определения кратного интеграла, имеем
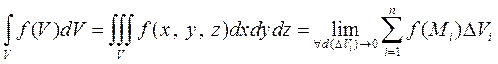 .
.
Замечание 1. Свойства тройного интеграла аналогичны свойствам крат-ного интеграла.
Определение. Правильной пространственной областью V называется область, удовлетворяющая следующим условиям:
1. Верхняя и нижняя границы области V задаются уравнениями: 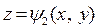 и
и 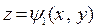 соответственно;
соответственно;
2. Всякая прямая, параллельная оси O z, пересекает верхнюю и нижнюю границы области V не более чем в двух точках;
 3. Проекция области V в плоскость O xy является правильной в направлении осей O y или O x областью D.
3. Проекция области V в плоскость O xy является правильной в направлении осей O y или O x областью D.
z

 V
V 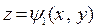
O y
a
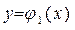
 D
D 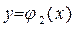
b
х
Если V правильная область, то можно показать, что вычисление тройного интеграла сводится к вычислению повторного интеграла
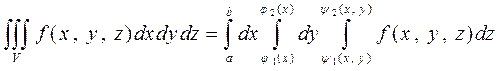 .
.
3.2. Замена переменных в тройном интеграле
Пусть заданы непрерывно дифференцируемые функции
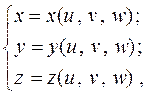
которые осуществляют взаимно однозначное отображение области 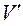 в координатах
в координатах 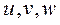 на область V в координатах
на область V в координатах 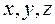 . Тогда аналогично, как и для двойного интеграла, получим формулу замены переменных в тройном интеграле
. Тогда аналогично, как и для двойного интеграла, получим формулу замены переменных в тройном интеграле
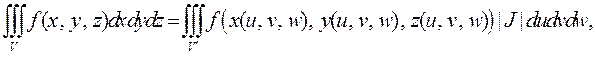 (1)
(1)
где определитель J = 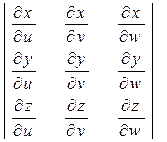 называется якобианом.
называется якобианом.
В качестве примера рассмотрим цилиндрические координаты. В цилиндрических координатах положение точки определяется координатами 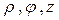 .
.
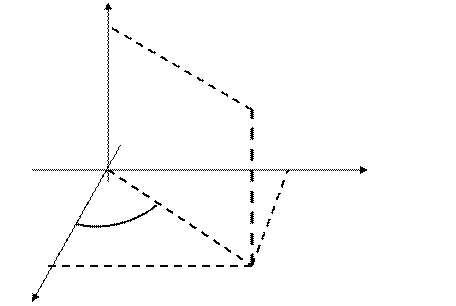
z
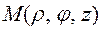
O y
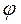
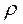
x
Из рисунка видна связь декартовых координат с цилиндрическими
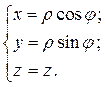
Если теперь в формуле (1) положить 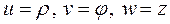 , то получим
, то получим 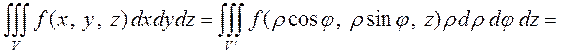
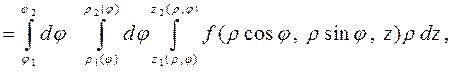
так как якобиан для цилиндрических координат имеет вид
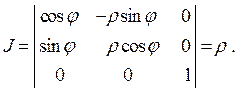
Здесь 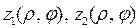 - уравнения нижней и верхней границ об-ласти V в цилиндрической системе координат, а
- уравнения нижней и верхней границ об-ласти V в цилиндрической системе координат, а 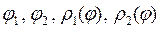 - границы области D в полярной системе координат.
- границы области D в полярной системе координат.
3.3. Приложения тройного интеграла
3.3.1. Объём тела.
Если положить 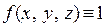 , то из определения тройного интеграла следует, что
, то из определения тройного интеграла следует, что
 Пример 1. Найти объём тела, ограниченного поверхностями:
Пример 1. Найти объём тела, ограниченного поверхностями: 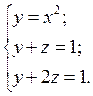
Изобразим данную область z
O 1 y
x
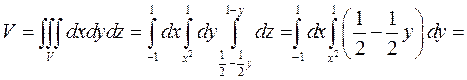

3.3.2. Центр масс (тяжести) тела.
Если 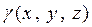 - плотность области V, то, как было показано ранее, масса тела будет равна
- плотность области V, то, как было показано ранее, масса тела будет равна
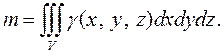
Рассуждая аналогично, как и для случая двойного интеграла находим координаты центра масс (тяжести)
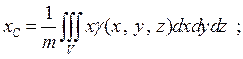
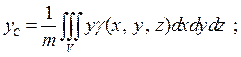
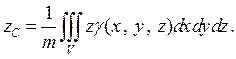 (2)
(2)
Замечание 2. Формулы (2) для однородного тела преобразуются аналогично, как и для случая двойного интеграла.
Пример 2. Найти координаты центра масс (тяжести) тела, ограничен-ного поверхностями: 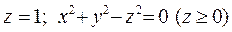 , если известна его плот-ность
, если известна его плот-ность 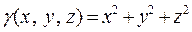 .
.
 z
z
O y
x
В цилиндрических координатах
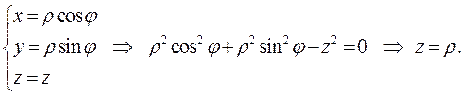
Тогда в силу симметрии тела и функции плотности относительно оси аппликат имеем х С = у С = 0 и
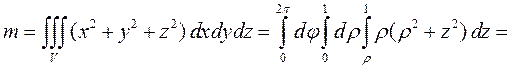
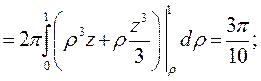
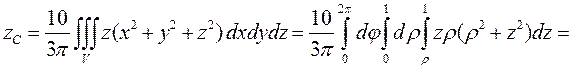

3.3.3. Моменты инерции.
Аналогично, как и для двойного интеграла, получаем выражения для моментов инерции относительно координатных осей
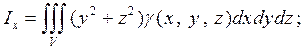
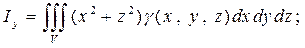
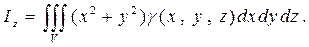
Пример 3. Найти момент инерции однородного бруса длиною l, a и b - размеры прямоугольного поперечного сечения.
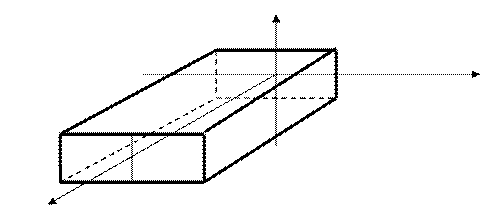
z
a
b y
x
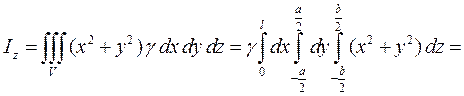
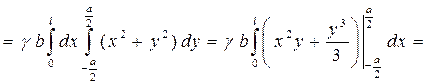
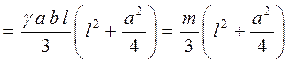 ,
,
где т - масса бруса.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 680; Нарушение авторских прав?; Мы поможем в написании вашей работы!