
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 52
|
|
|
|
2.3. Замена переменных в двойном интеграле.
Пусть координаты х и у являются функциями новых переменных и и v:
 (1)
(1)
где  и
и 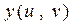 однозначные и непрерывные функции вместе со своими производными в некоторой области
однозначные и непрерывные функции вместе со своими производными в некоторой области 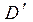 . По формуле (1) каждой точке
. По формуле (1) каждой точке 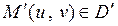 соответствует единственная точка
соответствует единственная точка 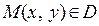 .
.
Верно и обратное.

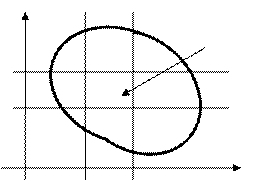 Таким образом, между областями D и
Таким образом, между областями D и 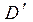 установлено взаимно одно-значное соответствие. Каждой линии вида
установлено взаимно одно-значное соответствие. Каждой линии вида 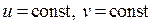 соответствуют некоторые кривые в плоскости O xy, а прямоугольной площадке
соответствуют некоторые кривые в плоскости O xy, а прямоугольной площадке 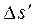 - криволинейная площадка
- криволинейная площадка 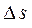 в области D.
в области D.
v y 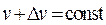
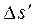
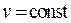
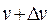
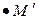
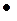 M
M
v
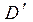
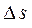 D
D
u x
O u 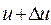 O
O 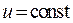
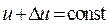
Рассмотрим интегральную сумму от функции 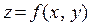 в области
в области
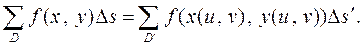 (2)
(2)
В формуле (2), чтобы получить интегральную сумму по области 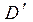 , необходимо выразить
, необходимо выразить 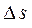 через
через 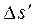 . Если вычислять
. Если вычислять 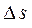 как площадь параллелограмма, то с точностью до б.м.в. более высокого порядка можно получить равенство
как площадь параллелограмма, то с точностью до б.м.в. более высокого порядка можно получить равенство 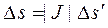 , где определитель
, где определитель 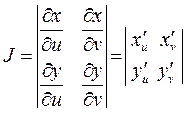 называется якобианом. Тогда равенство (2) принимает вид
называется якобианом. Тогда равенство (2) принимает вид
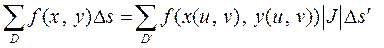 . (3)
. (3)
Переходя к пределу при 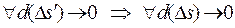 в интегральных суммах (3), получаем
в интегральных суммах (3), получаем
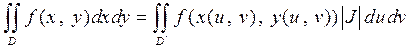 . (4)
. (4)
Формула (4) представляет собой формулу замены переменных в двой-ном интеграле.
Замечание 1. Так как 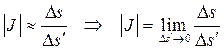 , то якобиан представ-ляет собой коэффициент изменения площади элементарной площадки.
, то якобиан представ-ляет собой коэффициент изменения площади элементарной площадки.
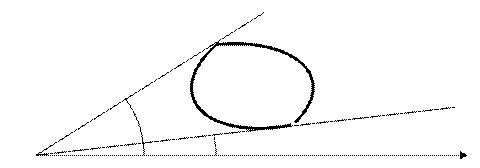
2.4. Двойной интеграл в полярной системе координат
Напомним связь между декартовыми и полярными координатами:
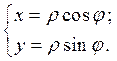
Вычислим якобиан для этого случая, полагая 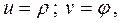
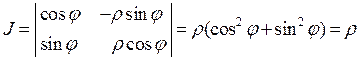 .
.
Тогда формула (4) для вычисления двойного интеграла примет вид
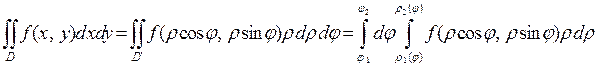 (5)
(5)
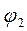
О 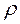
Замечание 2. Из геометрического смысла якобиана следует, что площадь элементарной площадки в полярной системе координат вычисляется по формуле 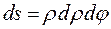 - элемент площади в полярной системе координат.
- элемент площади в полярной системе координат.
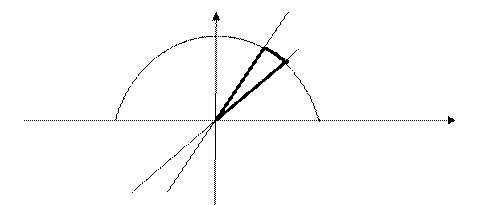
Пример 1. Вычислить двойной интеграл 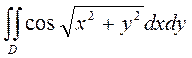 , пере-ходя к полярной системе координат, где область
, пере-ходя к полярной системе координат, где область 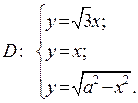
 у
у 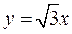
а 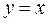
- а О а х
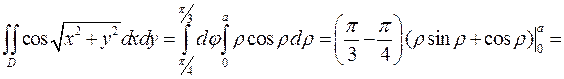
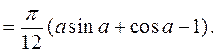
Пример 2. Вычислить интеграл Пуассона  .
.
 Рассмотрим область y
Рассмотрим область y
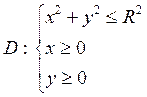 .
.
Перейдём к полярным
координатам.
Тогда О R x
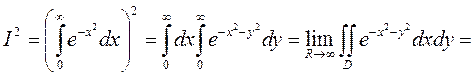
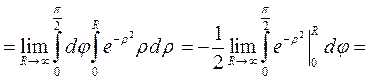
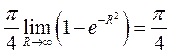 .
.
Таким образом, интеграл Пуассона 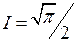 .
.
2.5. Приложения двойного интеграла
2.5.1. Площадь плоской области.
Если подынтегральная функция 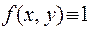 , то площадь области D в ДСК равна
, то площадь области D в ДСК равна 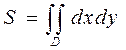 или
или 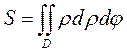 - в полярной системе координат, что следует из определения двойного интеграла.
- в полярной системе координат, что следует из определения двойного интеграла.
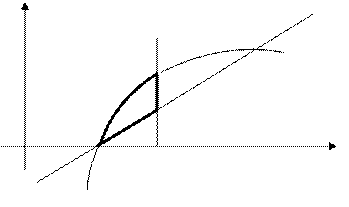 Пример 3. Найти площадь у
Пример 3. Найти площадь у 
области 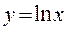
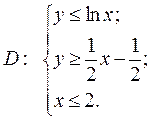 D
D
Изобразим данную О 2 х
область на рисунке и
вычислим ее площадь:
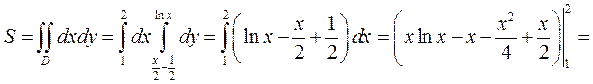
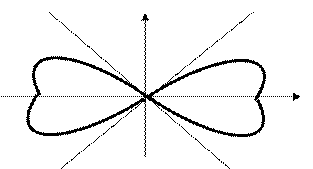
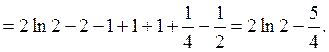
Пример 4*. Найти площадь у
фигуры, ограниченной линией 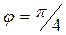
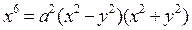 .
.
Изобразим данную область х
на рисунке.
Перейдём к полярной системе 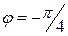
координат 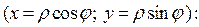
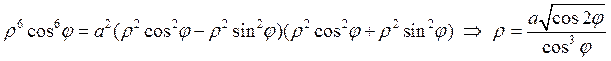 .
.
Из рисунка следует
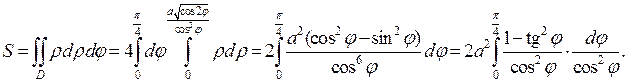
Для вычисления этого интеграла воспользуемся заменой 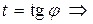
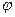
| 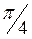
| |
| t |
и формулой  . Тогда имеем
. Тогда имеем
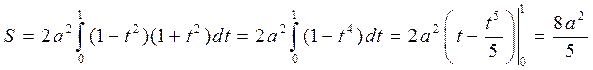 .
.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 379; Нарушение авторских прав?; Мы поможем в написании вашей работы!