Тема 4 : Интеграл от функции комплексной переменной

4.1. Определение интеграла

Пусть на некоторой линии L задана непрерывная функция 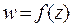. Разобьём кривую L на п частей y B

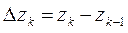. В каждой части

разбиения произвольно выберем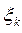

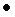
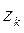
точку 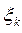и составим интегральную L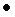

сумму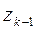

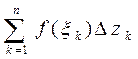. A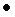

Тогда O x

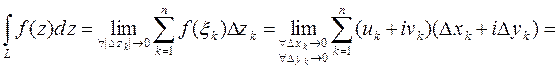
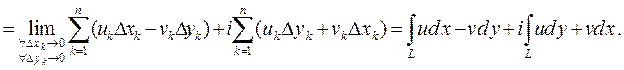
Таким образом, вычисление интеграла от функции комплексной переменной сводится к вычислению двух криволинейных интегралов от функци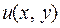й и 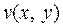действительных переменных. Из этого следует факт существования интеграла и его основные свойства:

1. Если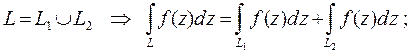

2. 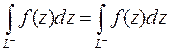, т.е. при изменении направления пути инте-грирования интеграл меняет знак;

3. Если 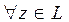выполняется

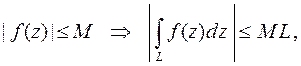
где L - длина линии.

Аналогично происходит и вычисление интеграла. Если линия

,

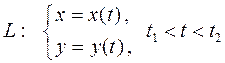т.е. 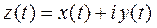и тогда

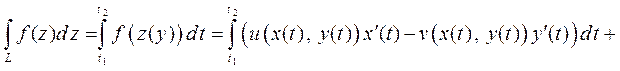
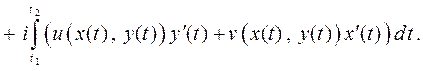
Пример 3. Вычислить 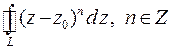, где контуром является окружность L: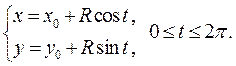

Представим уравнение окружности в комплексной форме

,

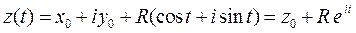тогда

.

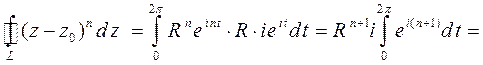
4.2. Основная теорема Коши

Теорема 2. Если 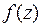однозначная и аналитическая функция в одно-связной области 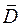, то для любой замкнутой линии 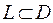выполняется

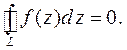
Представим интеграл в виде

и воспользуемся тем, что выражения 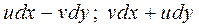из условий Коши – Римана являются полными дифференциалами. Тогда интеграл по замкнутой линии равен нулю, что и требовалось доказать.

Замечание 3. Верно и обратное утверждение (теорема Морера), т.е. если

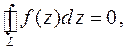
то 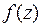- аналитическая функция.

На основании этой теоремы легко доказать следующую теорему.

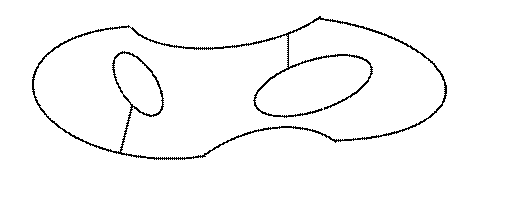
Теорема 3 (теорема Коши для сложного контура). Если функция 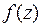однозначная и аналитическая в многосвязной области D, то выполняется

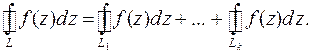
М

N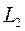

А

B D

Рисунок приведен для случая трехсвязной области. Для доказатель-ства данной теоремы необходимо сделать разрезы АВ и МN, а затем применить основную теорему Коши для полученной односвязной области.

Дата добавления: 2014-11-16