Лекция № 74. Тема 1 : Оригинал и изображение

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

1.1. Определение оригинала и изображения

Определение 1. Оригиналом называется функция 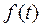действительной переменной t, удовлетворяющая следующим условиям:

1. 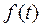однозначная и кусочно-непрерывная функция вместе со своими производными;

2.

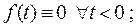
3. 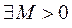и 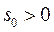, что выполняется 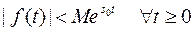, где 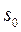называется показателем роста функции .

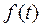Определение 2. Изображением оригинала 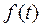называется функция 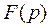комплексной переменной 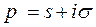, которая определяется интегра-лом Лапласа

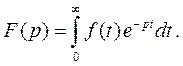(1)

Естественно, что при этом аргумент p должен быть таким, чтобы несобственный интеграл (1) был сходящимся, т.е. 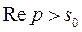. Интеграл (1) называется преобразованием Лапласа функции 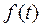и обозначается

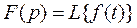или

Теорема об обращении преобразования Лапласа. Если 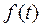оригинал и 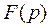его изображение, то 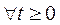имеет место формула обращения (обратное преобразование Лапласа)

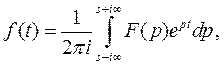(2)

где интегрирование ведется вдоль прямой 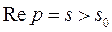, параллельной мнимой оси. Формулу (2) символически записывают

.

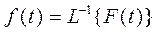Основные свойства преобразования Лапласа:

1. Преобразование Лапласа обладает свойством линейности, т.е.

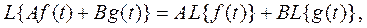
где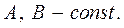

2. Всякое изображение 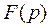при 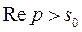является аналитической функцией;

3. Если 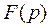- изображение функции 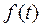, то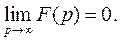

1.2. Изображения некоторых функций

1. Единичная функция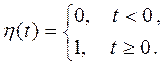

Тогда

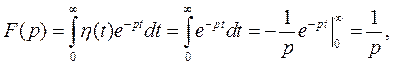
т.е. 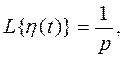если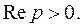

Замечание. Из определения преобразования Лапласа следует, что в дальнейшем преобразование Лапласа будет осуществляться для функций вида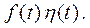

2. Степенная функция 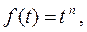где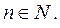

Найдем изображение функции 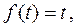т.е. рассмотрим случай, когда 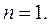Тогда имеем

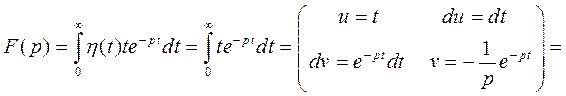
Аналогично, применяя формулу интегрирования по частям n раз, получим окончательную формулу

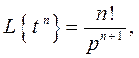если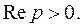

3. Показательная функция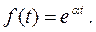

Аналогично получим 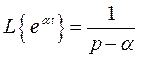, если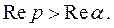

4. Гиперболические функции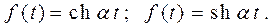

Так как

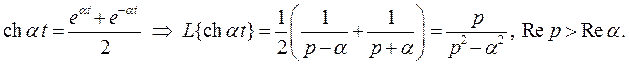
Аналогично получим

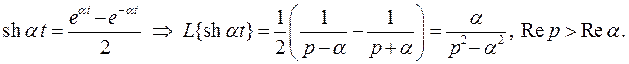
5. Тригонометрические функции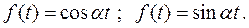

Как известно, тригонометрические функции можно выразить через показательные функции, поэтому получим

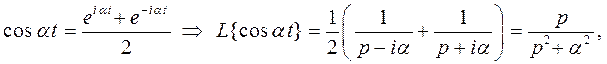
где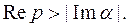

Аналогично имеем

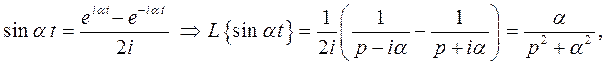
где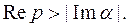

Все полученные результаты внесем в таблицу.

Оригинал	Изображение		Оригинал	Изображение

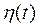
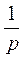
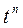
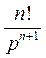
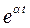
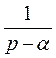
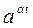
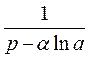
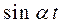
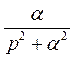
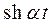
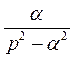
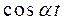
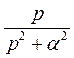
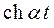
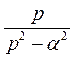
Пример 1. Найти изображение функции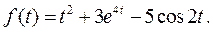

Используя свойство линейности преобразования Лапласа и таблицу изображений, получим

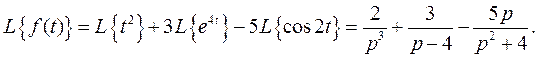
Дата добавления: 2014-11-16