
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энтропия правильно образованного кристалла любого индивидуального вещества при абсолютном нуле равна нулю
Постулат Планка позволяет ввести понятие абсолютной энтропии вещества ( ), т.е. энтропии отсчитанной от нулевого значения при Т = 0. Значения абсолютной энтропии ряда веществ приведены в приложении.
), т.е. энтропии отсчитанной от нулевого значения при Т = 0. Значения абсолютной энтропии ряда веществ приведены в приложении.
Третий закон термодинамики позволяет вычислить абсолютное значение энтропии для веществ в любом агрегатном состоянии, если известны экспериментальные значения теплоемкостей от 0 К до данной температуры, а также теплоты и температуры фазовых переходов. Так, уравнение для вычисления энтропии вещества в газообразном стандартном состоянии будет иметь вид:
 (36)
(36)
где индексы тв, ж, г относятся соответственно к твердому, жидкому и газообразному состоянию вещества.
Значение абсолютной энтропии вещества используют для расчёта изменения энтропии в химических реакциях:
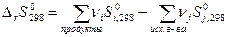 , (37)
, (37)
где  - стандартная энтропия веществ при Т = 298 К.
- стандартная энтропия веществ при Т = 298 К.
При расчете изменения энтропии в химической реакции, проходящей при любой другой температуре Т, используют уравнение
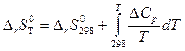 (38)
(38)
Характеристическими функциями называются такие функции состояния системы, посредством которых и их производных могут быть выражены в явной форме все термодинамические свойства системы. Характеристическими функциями являются внутренняя энергия (U), энтальпия (Н), энтропия (S), энергия Гельмгольца (W = U – TS), энергия Гиббса (G = H – TS = W + pV).
Особенность характеристических функций состоит в том, что свойством характеристичности они обладают лишь при определенном выборе независимых переменных, которые получили название естественных переменных. Для энергии Гельмгольца такими переменными являются V, T, для энергии Гиббса – Т, Р.
Энергия Гельмгольца и энергия Гиббса являются термодинамическими потенциалами, т.е. такими функциями состояния, убыль которых при обратимом переходе из состояния (1) в состояние (2) при двух постоянных параметрах (своих естественных переменных) равна полезной работе обратимого процесса (максимальной полезной работе, т.е не включает работу расширения).
Уравнения Гиббса-Гельмгольца связывают максимальную работу равновесных процессов с тепловыми эффектами неравновесных процессов, протекающих между теми же начальным и конечным состояниями, но без совершения работы или с совершением только работы расширения
 (39)
(39)
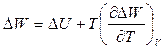 (40)
(40)
Можно показать, что если неизолированная изотермическая система не совершает работы ( ), то при Т, V = const
), то при Т, V = const
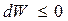 ,
,
а при Т, Р = const
 ,
,
т.е. самопроизвольный неравновесный процесс может идти только в сторону уменьшения энергии Гельмгольца (при Т, V = const) или энергии Гиббса (при Т, Р = const) системы, а равновесие наступает когда соответствующая энергия принимает минимальное значение (dW = 0 и ΔW = 0; или dG = 0 и ΔG = 0).
Отношение бесконечно малого изменения величины свободной энергии системы к бесконечно малому количеству компонента, внесенному в систему, есть химический потенциал μi данного компонента в системе:
 (41)
(41)
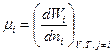 (42)
(42)
Химический потенциал компонента связан с его парциальным давлением или концентрацией следующими соотношениями:
 (43)
(43)
 (44)
(44)
где μ0i – стандартный химический потенциал компонента.
Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации (С), парциальные давления (P) или мольные доли (X) реагирующих веществ.
Для реакции:
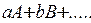 «
«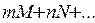
соответствующие константы равновесия выражаются следующим образом:
 (45)
(45)
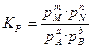 (46)
(46)
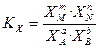 (47)
(47)
|
|
Дата добавления: 2014-11-16; Просмотров: 718; Нарушение авторских прав?; Мы поможем в написании вашей работы!