Простые движения

2.1 Основные задачи. Поступательное движение тела, основная теорема

Задачи кинематики твёрдого тела состоят в следующем:

1) задание движения и определение кинематических характеристик движения тела в целом; 2) определение кинематических характеристик движения отдельных точек тела.

Рассмотрим поступательное движение твердого тела. П оступательное движение твёрдого тела – это такое движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе.

Поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории точек могут быть любыми кривыми линиями.

Например:

1. Кузов автомобиля на прямолинейном участке дороги движется поступательно, при этом траектории его точек будут прямыми линиями.

2. Спарник АВ (рисунок 2.1) при вращении кривошипов О₁А и О₂В (О₁А=О₂В) движется поступательно (любая прямая, проведённая в нём, остаётся параллельной самой себе). Точки спарника при этом движутся по окружности:

А В

О₁ О₂

Рисунок 2.1

Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

Для доказательства рассмотрим твёрдое тело, совершающее поступательное движение относительно системы отсчёта OXYZ.

Рисунок 2.2

Выберем в теле произвольные точки А и В, положения которых в момент времени t определяются радиусами- векторам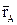и и 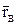(рисунок 2.2). Проведём вектор АВ, соединяющий эти точки, тогда

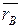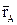= + (2.1)

Длина АВ неизменна, т. к. тело абсолютно твёрдое, направление АВ остаётся неизменным, т. к. тело движется поступательно. Поэтому, как видно из (2.1) траектория точки В получается из траектории точки А параллельным смещением всех её точек на постоянный вектор АВ. Следовательно, траектории точек А и В будут действительно одинаковыми кривыми.

Для нахождения скоростей точек А и В продифференцируем обе части равенства (2.1) по времени. Получим:

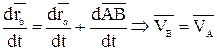, т. к. 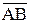= const. (2.2)

Таким образом, скорости точек А и В в любой момент времени одинаковы по величине и по направлению. Беря от обеих частей полученного равенства производные по времени, найдём

(2.3)

Следовательно, ускорение точек А и В тела в любой момент времени тоже одинаковы по величине и направлению.

Следовательно, теорема доказана.

Из данной теоремы можно сделать вывод, что для изучения поступательного движения абсолютно твёрдого тела достаточно изучить движение одной его точки.

2.2 Вращательное движение твёрдого тела вокруг оси

2.2.1 Угловая скорость и угловое ускорение тела

Вращательным движением твёрдого тела (вокруг неподвижной оси) называется такое движение, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях, и центры этих окружностей лежат на одной прямой, называемой осью вращения.

Для определения положения вращающегося тела проведём через ось вращения неподвижную плоскость 1 и подвижную плоскость 2, связанную с телом (рисунок 2.3).

Рисунок 2.3

В этом случае положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом j между этими плоскостями. Будем считать угол j положительным, если вращение происходит против часовой стрелки, и отрицательным, если по ходу часовой стрелки. Угол j измеряется в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла j от времени, т.е.

j = f (t) (2.4)

Уравнение (2.4) выражает закон вращательного движения твёрдого тела вокруг неподвижной оси.

Кинематические характеристики вращательного движения тела – угловая скорость w и угловое ускорение x:

(2.5)

(2.6)

Угловая скорость характеризует быстроту изменения угла поворота тела j;

Угловое ускорение характеризует быстроту изменения угловой скорости тела w.

Если угловая скорость w и угловое ускорение тела ξ имеют одинаковые знаки, то вращение равноускоренное, и если разные, то – равнозамедленное:

w > 0; x > 0; w < 0; x < 0 – равноускоренное вращение.

w > 0; x < 0; w < 0; x > 0 – равнозамедленное вращение.

Таким образом, кинематические характеристики вращающегося тела – угловая скорость w и угловое ускорение x.

2.2.2 Скорости и ускорения точек вращающегося тела

1) Скорости точек тела

Рассмотрим точку М тела, которая находится на расстоянии h от оси вращения (рисунок 2.3). При вращении точка М будет описывать окружность радиусом h, плоскость которой перпендикулярна оси вращения z, а центр С лежит на самой оси. Если за время dt тело повернётся на угол dj, то точка М при этом совершит вдоль своей траектории элементарное перемещение dS = hdj, тогда числовое значение скорости точки будет:

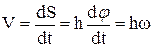(2.7)

Скорость V называют линейной или окружной скоростью точки М т.о. численное значение скорости точки вращающегося твёрдого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.

Направлена скорость V по касательной к окружности, описываемой точкой, перпендикулярно плоскости, проходящей через ось вращения и точку М. Т.к. для всех точек тела в данный момент времени угловая скорость w одинакова, то из формулы (2.7) следует, что скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Поле скоростей точек вращающегося тела имеет вид; показанный на рисунке 2.4.

μ

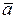
w

С

w

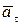
с x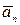

Рисунок 2.4 Рисунок 2.5

2) Ускорение точек тела

Для нахождения ускорения точки М воспользуемся формулами:

a _τ a _n =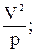

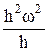В нашем случае p = h., тогда получим: a _τ = h a _n = или

a _τ = hx (2.8)

a _n = hw² (2.9)

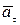– направлен по касательной к траектории по направлению x, а 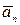направлен всегда по радиусу МС к оси вращения (рисунок 2.5).

полное ускорение точки М будет:

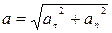(2.10)

или a = h 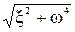(2.11)

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности, определяется углом m который вычисляется по формуле:

tgm= 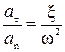(2.12)

Т.к. w и x в данный момент времени для всех точек тела имеют одно и то же значение, то из формулы (2.11) и (2.12) следует, что ускорение всех точек вращающегося тела пропорциональны их расстояниям до оси вращения и образуют один и тот же угол m с радиусами описываемых ими окружностей (рисунок 2.6).

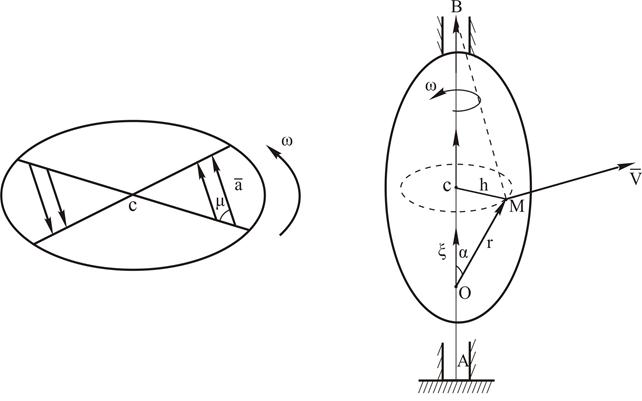
Рисунок 2.6 Рисунок 2.7

2.2.3 Векторы скорости и ускорения точек тела

Чтобы найти выражения для векторов и 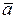, проведём из произвольной точки О оси АВ радиус-вектор 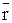точки М. Тогда h=rsina, поэтому 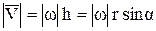или

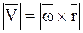(2.13)

Таким образом, модуль векторного произведения равен модулю скорости точки М. Направления и тоже совпадают (оба перпендикулярны плоскости ОМВ), следовательно 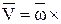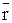, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Формулу (2.13) называют формулой Эйлера.

Беря от обеих частей равенства (2.13) производные по времени, получим формулу:

или 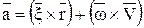(2.14)

Формула (2.14) определяет вектор ускорения любой точки вращающегося тела. Вектор 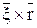направлен, так же как и вектор , т.е. по касательной к траектории точки М, т.е.

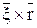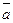= _t, (2.15)

а вектор 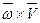направлен вдоль МС, т.е.

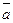= _n. (2.16)

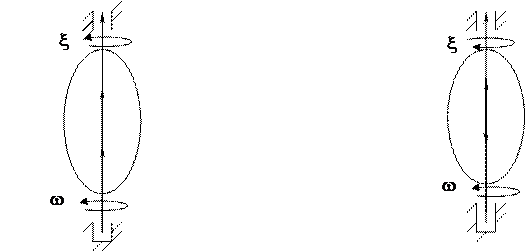
Z Z

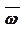
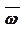
w > 0 w > 0

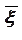
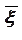
ускоренное замедленное вращение вращение

О О

Рисунок 2.8

Направление 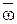определяем по правилу векторного произведения (2.13). Вектор 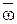направлен перпендикулярно плоскости, в которой расположены векторы, входящие в векторное произведение, и в ту сторону, откуда вращение тела наблюдается против хода часовой стрелки.

Вопросы для самоконтроля

1. Приведите примеры простых движений твердого тела.

2. Какое движение твердого тела называется поступательным?

3. Сформулируйте основную теорему поступательного движения тела.

4. Запишите кинематические уравнения поступательного движения твердого тела.

5. Какое движение твердого тела называется вращательным вокруг неподвижной оси?

6. Запишите уравнение вращения твердого тела вокруг неподвижной оси.

7. Тело вращается вокруг неподвижной оси по закону рад. Определите его угловую скорость и угловое ускорение в момент времени t = 0,5 с.

8. При равномерном вращении моховик совершает 2 оборота в минуту. За какое время маховик повернется на угол φ = 16π рад?

9. Скорость точки тела, которая находится на расстоянии R = 0,5 м от оси вращения, изменяется по закону V = 3t м/с. Определить угловое ускорение тела.

10. Тело вращается вокруг неподвижной оси по закону φ = 2t³ рад. Определить нормальное ускорение точки тела, которая находится на расстоянии 0,4 м от оси вращения, в момент времени t = 5 с.

11. Тело вращается вокруг неподвижной оси по закону φ = (3,5t²–2t) рад. Определить в момент времени t = 2 с тангенциальное ускорение точки тела, которая находится на расстоянии 0,2 м от оси вращения.

12. Тело вращается вокруг неподвижной оси по закону φ = (4 t² – 8t + 5) рад. Определить в момент времени t = 1 с ускорение точки тела, которая находится на расстоянии 0,5 м от оси вращения.

13. Дайте короткую характеристику вектора угловой скорости.

14. Запищите формулу Эйлера, проанализируйте ее.

15. Запишите векторную формулу для определения тангенциального ускорения точки вращающегося тела.

16. Запишите векторную формулу для определения нормального ускорения точки вращающегося тела.

17. Как вращается твердое тела, если векторы угловой скорости и углового ускорения имеют одинаковое направление?

18. Как вращается твердое тело, если векторы угловой скорости и углового ускорения направлены навстречу друг другу.

Дата добавления: 2014-11-08