
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плоскопараллельное движение твёрдого тела
|
|
|
|
3.1 Определение. Примеры. Уравнения движения
Плоскопараллельным (плоским) называется такое движение твёрдого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости.
Плоские движения совершают многие части механизмов и машин, например:
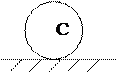 |
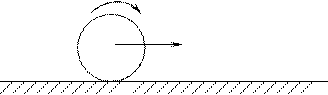
 1) катящееся колесо на прямолинейном участке пути:
1) катящееся колесо на прямолинейном участке пути:
А 
2) шатун АВ в кривошипно- шатунном механизме О В
3) звено АВ в спарнике  А В
А В
О1 О2
Частным случаем плоскопараллельного движения является вращательное движение твёрдого тела вокруг неподвижной оси.
Рассмотрим сечение S тела плоскостью OXY, параллельной неподвижной плоскости П (рисунок 3.1). При плоскопараллельном движении все точки тела, лежащие на прямой АВ, перпендикулярной сечению S, т.е. плоскости П, движутся тождественно.
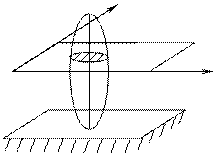 А У
А У
S
О Х
|
В
Рисунок 3.1
Таким образом, для изучения движения всего тела достаточно изучить движение плоской фигуры S, поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в её плоскости, т.е в плоскости ОХУ.
Положение плоской фигуры S в плоскости OXY определяется положением какого-нибудь проведённого на этой фигуре отрезка АВ (рисунок 3.2), а положение этого отрезка можно определить, зная координаты XA и YA точки А и угол j, который отрезок АВ образует с осью Х. Точку А, выбранную для определения положения фигуры S, называют полюсом.
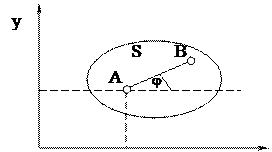 |
yА
O xА x
Рисунок 3.2
При движении фигуры величины ХА, УА, j будут изменяться. Чтобы знать закон движения фигуры S, т.е. её положение в любой момент времени в плоскости ОХУ, надо знать зависимости:
xА=f1(t); yА=f2(t); j=f3(t). (3.1)
Уравнения (3.1) являются уравнениями движения плоской фигуры в её плоскости или уравнениями плоскопараллельного движения тела.
3.2 Разложение плоского движения твёрдого тела на простые.
Кинематические характеристики
Рассмотрим движение плоской фигуры (рисунок 3.3); например два её положения – I и II, определяемые положениями отрезка АВ.
Перемещение плоской фигуры из I в II можно заменить двумя простыми плоскими перемещениями - поступательным и вращательным, которые можно выполнять по отдельности или одновременно.

 y В2 В1
y В2 В1


1 2
 |
А А1
I II
 0 x
0 x
Рисунок 3.3
Таким образом, плоскопараллельное движение фигуры представляет собой совокупность двух движений, происходящих одновременно: поступательного движения всех точек фигуры вместе с полюсом (например: точка А) и вращательного движения всех точек фигуры вокруг полюса.
Исходя из уравнения (3.1) кинематическими характеристиками плоского движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса (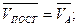
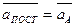 ), а также угловая скорость w и угловое ускорение x вращательного движения вокруг полюса.
), а также угловая скорость w и угловое ускорение x вращательного движения вокруг полюса.
Если за полюс выбрать любую другую точку фигуры, то кинематические характеристики поступательного движения изменяются, а кинематические характеристики вращательного движения останутся неизменными, т.е. вращательная часть плоского движения от выбора полюса не зависит.
3.3 Векторная формула для вычисления скоростей точек плоской фигуры
В п. 3.2 было показано, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью полюса – Va и из вращательного движения всех точек фигуры вокруг этого полюса.
Покажем, что скорость любой точки В плоской фигуры складывается геометрически из скоростей, которые точка приобретает в каждом из этих движений.
Рассмотрим плоскую фигуру, свяжем радиусами-векторами точки А и В этой фигуры с осями ОХУ:


 y
y 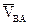
 В
В 
VA

|
 rA
rA
Рисунок 3.4
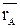 – радиус-вектор полюса А;
– радиус-вектор полюса А;
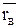 – радиус-вектор произвольной точки В.
– радиус-вектор произвольной точки В.
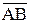 – вектор, определяющий положение точки В относительно осей AX1Y1, перемещающихся вместе с полюсом А поступательно.
– вектор, определяющий положение точки В относительно осей AX1Y1, перемещающихся вместе с полюсом А поступательно. 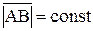 , т.к. фигура твёрдая, тогда
, т.к. фигура твёрдая, тогда 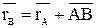 , продифференцировав по времени, получим
, продифференцировав по времени, получим
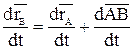 или
или 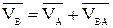 , (3.2)
, (3.2)
где 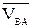 – это скорость, которую приобретает точка В при вращении фигуры вокруг полюса А, поэтому
– это скорость, которую приобретает точка В при вращении фигуры вокруг полюса А, поэтому
VВА=wAB, (3.2 / )
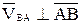 , где w – угловая скорость фигуры.
, где w – угловая скорость фигуры.
Таким образом, скорость произвольной точки В плоской фигуры геометрически складывается из скорости какой-либо другой точки А, принятой за полюс, и скорости, которую точка В получает при вращении фигуры вокруг этого полюса; т.е.
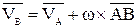 . (3.3)
. (3.3)
В выражении (3.2) присутствуют кинематические характеристики как поступательного, так и вращательного движений, что ещё раз подчеркивает, что плоское движение – это сложное движение, являющееся совокупностью поступательного и вращательного движений.
Модуль и направление 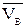 определяются построением соответствующего параллелограмма (рисунок 3.5).
определяются построением соответствующего параллелограмма (рисунок 3.5).
Рассмотрим, например, колесо, катящееся по прямолинейному отрезку пути без скольжения; центр колеса точка С имеет скорость 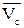 . Выберем две произвольные точки В и D на ободе колеса и, используя выражение (3.3), запишем их скорости:
. Выберем две произвольные точки В и D на ободе колеса и, используя выражение (3.3), запишем их скорости:
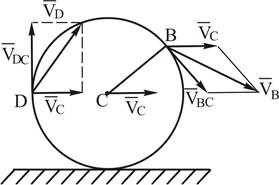
Рисунок 3.5
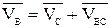 ;
; 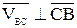 ;
;
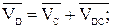
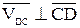 . (3.4)
. (3.4)
Чтобы вычислить численные значения скоростей точек В и D, используют теорему косинусов, для чего необходимо знать углы между векторами 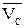 и
и 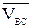 ;
; 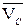 и
и 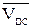 .
.
3.4 Векторная формула для вычисления ускорения точек плоской фигуры
Покажем, что ускорение любой точки В плоской фигуры (так же как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры.
Рассмотрим плоскую фигуру с полюсом в точке А.
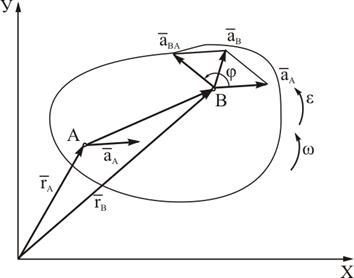
Рисунок 3.6
Продифференцируем дважды по времени (3.2) и получим:
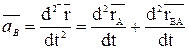 или
или 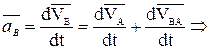
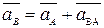 (3.5)
(3.5)
или 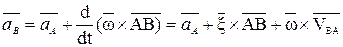 ,
,
где 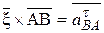 ;
; 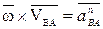 ; (3.6)
; (3.6)
или  (3.5 /)
(3.5 /)
Таким образом, ускорение произвольной точки плоской фигуры В геометрически складывается из ускорения полюса 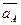 и ускорения, которое точка В получает при вращении фигуры вокруг этого полюса.
и ускорения, которое точка В получает при вращении фигуры вокруг этого полюса.
Модуль и ускорение 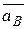 находятся построением соответствующего параллелограмма (рисунок 3.6).
находятся построением соответствующего параллелограмма (рисунок 3.6).
Однако вычисление 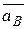 с помощью параллелограмма изображённого на рисунке 3.6, осложняется нахождением угла φ между векторами
с помощью параллелограмма изображённого на рисунке 3.6, осложняется нахождением угла φ между векторами 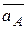 и
и 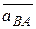 , поэтому
, поэтому 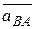 удобнее заменять его касательной (
удобнее заменять его касательной (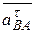 ) и нормальной (
) и нормальной (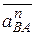 ) составляющими, (3.6).
) составляющими, (3.6).
Следует отметить, что 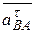 совпадает по направлению с x и
совпадает по направлению с x и 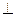
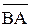 , а
, а 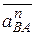
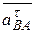 и направлен от точки В к точке А, величины их вычисляются по формулам:
и направлен от точки В к точке А, величины их вычисляются по формулам:
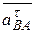 =АВx;
=АВx; 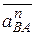 =АВw2. См. рисунок 3.7.
=АВw2. См. рисунок 3.7.
Если полюс А движется не прямолинейно, то его ускорение можно тоже представить как сумму касательной и нормальной составляющей, тогда можно записать:
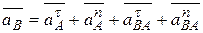 (3.7)
(3.7)
Формулы 3.5–3.7 обычно используют при решении задач.
|
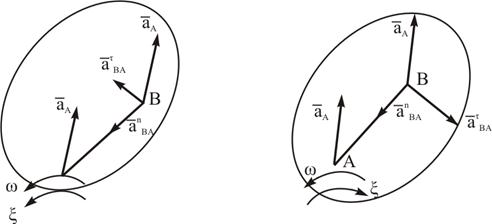
Рисунок 3.7
3.5 Определение скоростей точек плоской фигуры с помощью мгновенного
центра скоростей (М.Ц.С)
Другой более простой и наглядный метод определения скоростей точек тела при плоском движении основан на понятии о мгновенном центре скоростей.
М.ц.с- это такая точка в плоскости плоской фигуры, скорость которой в данный момент времени равна нулю. Обозначают её Р. В данный момент времени это единственная точка, скорость, которой равна нулю.
Способы определения м.ц.с:
1) если плоскопараллельное движение осуществляется путём качения без скольжения цилиндрического тела по какой-либо неподвижной поверхности, то точка соприкосновения катящегося тела с поверхностью имеет скорость, равную нулю, следовательно, является м.ц.с. Примером служит качение колеса по рельсу.
 w
w
с 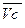
 |
|
|
|
Дата добавления: 2014-11-08; Просмотров: 971; Нарушение авторских прав?; Мы поможем в написании вашей работы!