Динамика механической системы

2.1 Механическая система. Силы внешние и внутренние

Механической системой называется совокупность материальных точек или тел, взаимодействующих между собой по принципу действия и противодействия.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п., т.е. различными геометрическими связями. В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в небе самолетов), механическую систему не образуют. В дальнейшем мы будем рассматривать только механические системы и называть их просто системами.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними силами называют силы взаимодействия между материальными точками данной механической системы. Примером внутренних сил могут служить силы упругости, действующие между частицами упругого тела, принятого за механическую систему.

Внешние силы условимся обозначать 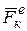; а внутренние - 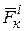. Одна и та же сила может быть как внешней, так и внутренней в зависимости от того, какая механическая система рассматривается. Так, например, реакции подшипников вала являются внешними силами относительно вала. Эти же реакции относятся к внутренним силам, когда рассматривается вся установка вместе со станиной. Таким образом, любая сила, действующая на точку механической системы является внешней или внутренней, и в то же время она является задаваемой силой или реакцией связи. Движение точек механической системы зависит как от внешних, так и от внутренних сил.

На основании закона действия и противодействия следуют свойства внутренних сил:

1. Главный вектор всех внутренних сил системы и суммы их проекций на координатные оси равны нулю:

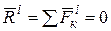
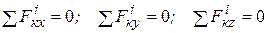(2.1)

2. Главные моменты всех внутренних сил системы относительно любого центра и координатных осей равны нулю:

(2.2)

Хотя уравнения (2.1) и (2.2) имеют вид уравнений равновесия сил, произвольно расположенных в пространстве, внутренние силы не уравновешиваются, так как они приложены к различным точкам системы и могут вызывать перемещения этих точек относительно друг друга. Уравновешенной вся совокупность внутренних сил будет у системы, представляющей собой абсолютно твердое тело.

2.2 Центр масс системы материальных точек и его координаты

Каждая точка М_к механической системы имеет определенную массу m_к, а ее положение относительно системы отсчета Охуz в каждый момент времени определяется радиусом-вектором или тремя координатами .

Центром масс системы, состоящей из n точек, называется геометрическая точка С, радиус-вектор которой

, (2.2.1)

где 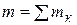- масса системы (рисунок 2.1).

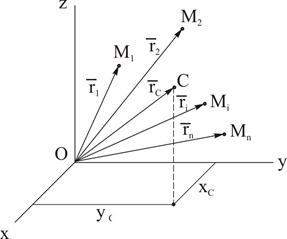
Рисунок 2.1

Проецируя векторы обеих частей равенства (2.2.1) на оси х, у, z, получаем формулы, определяющие координаты центра масс системы:

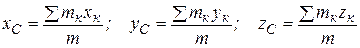. (2.2.2)

Как видно из формул (2.2.1) и (2.2.2) положение центра масс системы в каждый момент времени зависит только от положения и массы каждой точки этой системы. Центр тяжести тела или системы тел является центром масс этой системы: (см. «Статика»)

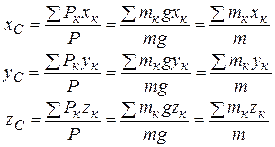(2.2.2^/)

Действительно, центр тяжести системы тел совпадает с их центром масс. Понятие «центр масс системы» применимо для любой системы материальных точек независимо от того, находится ли она под действием каких-либо сил или нет, тогда как понятие «центр тяжести» применяется лишь для твердого тела или системы твердых тел, находящихся в однородном поле сил тяжести.

2.3 Абсолютно твердое тело. Моменты инерции твердого тела.

Радиус инерции. Теорема Гюйгенса.

Под абсолютно твердым телом понимается система из бесконечно большого числа материальных точек, расстояния между которыми остаются неизменными (в теоретической механике рассматриваемые тела считаются абсолютно твердыми).

При поступательном движении твердого тела, так же как и при движении материальной точки, мерой его инертности является масса тела. При вращательном движении твердого тела мерой инертности является момент инерции твердого тела относительно оси вращения.

Моментом инерции тела (системы) относительно данной оси Оz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси:

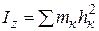. (2.3.1)

Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю. Для вычисления осевых моментов инерции можно расстояния точек от осей выражать через координаты х_к, у_к, z_к этих точек (например, квадрат расстояния от оси О_х будет 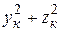и т.д.) тогда моменты инерции относительно осей Охуz будут определяться формулами:

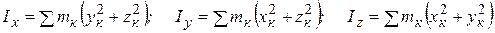(2.3.2)

Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси О_z называется линейная величина 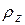, определяемая равенством

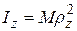, (2.3.3)

где М – масса тела.

Из определения следует, что радиус инерции геометрически равен расстоянию от оси О_z той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела. Зная радиус инерции, можно по формуле (2.3.3) найти момент инерции тела и наоборот.

Формулы (2.3.1) и (2.3.2) справедливы как для твердого тела, так и для любой системы материальных точек. В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе, сумма, стоящая в равенстве (2.3.1) обратится в интеграл. В результате, учитывая, что 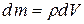, где ρ – плотность, а V – объем, получим

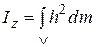или 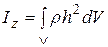(2.3.4)

Интеграл здесь распространяется на весь объем V тела, а плотность ρ и расстояние h зависят от координат точек тела. Аналогично формулы (2.3.2) для сплошных тел примут вид:

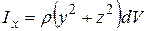и т.д. (2.3.5)

Формулами (2.3.4) и (2.3.5) удобно пользоваться при вычислении моментов инерции однородных тел правильной формы. При этом плотность ρ будет постоянной и выйдет из-под знака интеграла.

Моменты инерций некоторых однородных тел:

1. Тонкий однородный стержень длиной l и массой М.

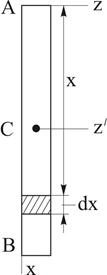Вычислим его момент инерции относительно оси А_z, перпендикулярной стержню и проходящей через его конец А (рисунок 2.2). Направим вдоль АВ координатную ось Ах, тогда для любого элементарного отрезка длины dx величина h=x, а масса 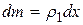, где - масса единицы длины стержня. В результате формула (2.3.5) дает:

,

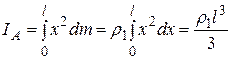заменяя 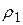его значением, найдем окончательно

Рисунок 2.2

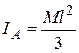. (2.3.6)

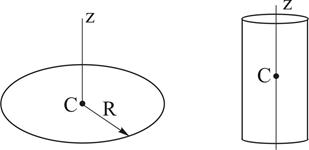2. Круглая однородная пластина или цилиндр радиусом R и массой М (ось z направлена вдоль оси цилиндра).

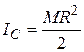(2.3.7)

Рисунок 2.3

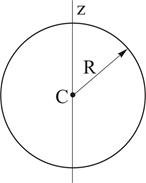
3. Сплошной шар массой М и радиусом R (ось z направлена вдоль диаметра).

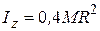(2.3.8)

Рисунок 2.4

При решении задач полезна теорема Гюйгенса о моменте инерции тела относительно параллельных осей: момент инерции тела относительно данной оси, равен моменту инерции тела относительно оси, ей параллельной и проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

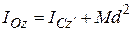. (2.3.9)

Например, для тонкого однородного стержня длиной l и массой М момент инерции относительно оси Сz ^/ (рисунок 2.2)

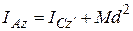, где ,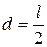

тогда или .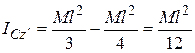

Из формулы (2.3.9) следует, что из всех осей данного направления наименьший момент инерции будет относительно той оси, которая проходит через центр масс.

Вопросы для самоконтроля

1. Как классифицируют в динамике силы, действующие на точки механической системы?

2. Что называют центром масс системы точек и как определяют его координаты?

3. Что называется осевым моментом инерции твердого тела?

4. Какую величину называют радиусом инерции тела?

5. В чем заключается теорема Гюйгенса?

Дата добавления: 2014-11-08