
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема о движении центра масс механической системы
|
|
|
|
3.1 Дифференциальные уравнения движения механической системы
Рассмотрим механическую систему, состоящую из n материальных точек. Выделим какую-нибудь точку системы с массой mк. Обозначим равнодействующую всех приложенных к точке внешних сил (и активных реакций связей) через 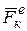 , а равнодействующую всех внутренних сил – через
, а равнодействующую всех внутренних сил – через 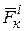 (рисунок 3.1). Если
(рисунок 3.1). Если 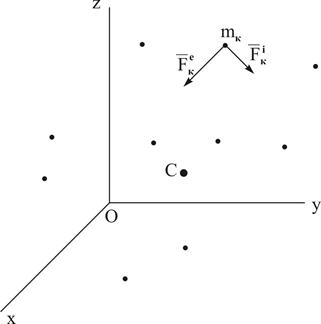 точка имеет при этом ускорение
точка имеет при этом ускорение  , то по основному закону динамики
, то по основному закону динамики
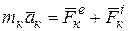 . (3.1)
. (3.1)
Уравнение (3.1) представляет собой дифференциальное уравнение движения к й точки. Проецируя векторы обеих частей равенства (3.1) на оси х, у, z; получим дифференциальные уравнения движения системы в проекциях на эти оси:
Рисунок 3.1
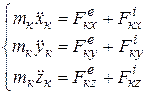 . (3.2)
. (3.2)
Для механической системы, имеющей n точек, получим 3n совместных дифференциальных уравнений движения. Так как внутренние силы, приложенные к точкам системы, в большинстве случаев остаются неизвестными, а число точек системы обычно велико, то эти 3n уравнений могут быть проинтегрированы лишь в исключительных случаях, поэтому используют другой способ для решения задач на движение системы тел.
3.2 Теорема о движении центра масс механической системы
В ряде случаев для определения характера движения системы (обычно твердого тела) требуется знать закон движения ее центра масс. Чтобы найти этот закон, составим уравнения движения для всех точек системы в виде (3.1) и сложим почленно их левые и правые части. Тогда получим:
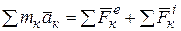 (3.3/)
(3.3/)
преобразуем левую часть этого равенства. Из формулы (2.2.1) для радиуса-вектора центра масс имеем
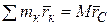 .
.
Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме производных, найдем
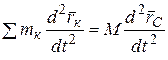
или 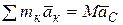 (3.3)
(3.3)
где 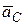 - ускорение центра масс системы.
- ускорение центра масс системы.
Так как по свойству внутренних сил системы 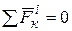 , получим окончательно из равенства (3.3/), учтя (3.3)
, получим окончательно из равенства (3.3/), учтя (3.3)
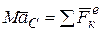 (3.4)
(3.4)
т.е. произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.
Уравнение (3.4) выражает теорему о движении центра масс системы, которая формулируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
Проецируя обе части векторного равенства (3.4) на оси х,у,z, получаем три уравнения в проекциях на оси координат:
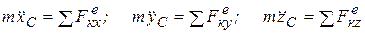 (3.5)
(3.5)
Уравнения (3.5) представляют собой дифференциальные уравнения движения центра масс. Из уравнений (3.4) и (3.5) следует, что внутренние силы непосредственно не влияют на движение центра масс, в связи с чем уравнения (3.4) и (3.5) имеют больше практическое значение.
Из кинематики известно, что поступательное движение твердого тела полностью определяется движением одной из его точек. Следовательно, решив задачу о движении центра масс тела как материальной точки массой, равной массе всего тела, можно определить поступательное движение всего тела.
Следствия из теоремы:
1. Если главный вектор внешних сил (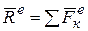 ) остается все время равным нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
) остается все время равным нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
Из (3.4) если  , то
, то  , т.е.
, т.е. 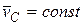 . При этом, если
. При этом, если 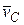 центра масс равна нулю, то центр масс находится в покое. Если же
центра масс равна нулю, то центр масс находится в покое. Если же 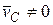 , то центр масс движется равномерно и прямолинейно с этой скоростью.
, то центр масс движется равномерно и прямолинейно с этой скоростью.
2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось остается все время равной нулю, то проекция центра масс механической системы на эту ось неподвижна или движется равномерно, т.е. если 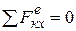 , то
, то  , т.е.
, т.е. 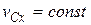 ; если
; если  , то
, то 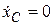 и
и 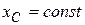 . Следствия из теоремы о движении центра масс системы выражают закон сохранения движения центра масс системы.
. Следствия из теоремы о движении центра масс системы выражают закон сохранения движения центра масс системы.
Вопросы для самоконтроля
1. Сформулируйте теорему о движении центра масс системы.
2. Какое движение твердого тела можно рассматривать как движение материальной точки, имеющей массу данного тела. Почему?
3. При каких условиях центр масс системы находится в состоянии покоя, и при каких условиях он движется равномерно и прямолинейно?
4. При каких условиях центр масс системы не перемещается вдоль некоторой оси?
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 2244; Нарушение авторских прав?; Мы поможем в написании вашей работы!