
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие теоремы динамики. 4.1 Теорема об изменении количества движения механической системы
|
|
|
|
4.1 Теорема об изменении количества движения механической системы
Одной из основных динамических характеристик движения является количество движения.
Количеством движения материальной точки называется векторная величина 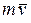 , равная произведению массы точки на ее скорость. Направлен вектор
, равная произведению массы точки на ее скорость. Направлен вектор 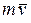 так же, как и скорость точки, т.е. по касательной к траектории.
так же, как и скорость точки, т.е. по касательной к траектории.
Количеством движения механической системы называется векторная величина 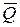 , равная геометрической сумме (главному вектору) количеств движения всех точек этой системы.
, равная геометрической сумме (главному вектору) количеств движения всех точек этой системы.
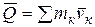 (4.1)
(4.1)
или 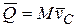 (4.1/)
(4.1/)
где 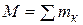 - масса системы точек;
- масса системы точек;
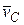 - скорость центра масс системы,
- скорость центра масс системы,
т.е. количество движения системы равно произведению массы всей системы М на скорость ее центра масс v C. Этой формулой особенно удобно пользоваться при вычислении количеств движения системы (тел), совершающих поступательное движение.
Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Сначала введем понятие об элементарном импульсе, т.е. об импульсе за элементарный промежуток времени dt.
Элементарным импульсом силы называется векторная величина 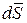 , равная произведению силы
, равная произведению силы 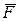 на элементарный промежуток времени dt:
на элементарный промежуток времени dt:
 (4.2)
(4.2)
При решении практических задач важное значение имеет связь между количеством движения системы и силами, действующими на данную механическую систему. Найдем эту связь, продифференцировав по времени выражение (3.1/):
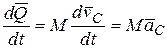
т.к. 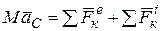 (
(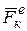 и
и 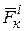 - внешние и внутренние силы, действующие на точки системы). По свойству внутренних сил
- внешние и внутренние силы, действующие на точки системы). По свойству внутренних сил 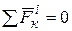 , тогда получим:
, тогда получим:
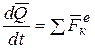 . (4.3)
. (4.3)
Уравнение (4.3) выражает теорему об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. Векторному уравнению (4.3) соответствуют три уравнения в проекциях на оси координат
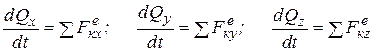 . (4.4)
. (4.4)
Уравнения (4.4) показывают, что производная по времени от проекции количества движения механической системы на любую ось равна проекции главного вектора внешних сил, действующих на систему, на ту же ось. Из уравнений (4.3) и (4.4) следует, что изменение количества движения механической системы вызывается только внешними силами.
Найдем другое выражение теоремы. Пусть в момент времени t = 0количество движения системы равно 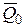 , а в момент времени t 1 становится равным
, а в момент времени t 1 становится равным 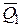 , тогда разделяя переменные в (4.3) и интегрируя, получим
, тогда разделяя переменные в (4.3) и интегрируя, получим
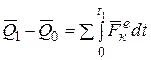 , или
, или
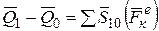 , (4.5)
, (4.5)
где 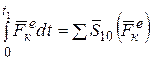 - импульс внешних сил, действующих на систему.
- импульс внешних сил, действующих на систему.
Выражение (4.5) представляет собой теорему об изменении количества движения механической системы в интегральной форме: изменение количества движения механической системы за данный промежуток времени равно геометрической сумме импульсов внешних сил, действующих на систему за тот же промежуток времени.
Векторному уравнению (4.5) соответствуют три уравнения в проекциях на оси координат:
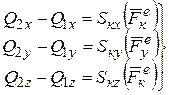 (4.6)
(4.6)
Уравнения (4.6) показывают, что изменение проекции количества движения механической системы на любую ось равно сумме проекций импульсов всех внешних сил, действующих на систему, на ту же ось.
При решении задач обычно пользуются уравнениями (4.6), которые так же как и уравнения (4.4) не содержат внутренних сил, что имеет большое практическое значение. По аналогии записываются теоремы об изменении количества движения для материальной точки.
Следствия из теоремы:
1. Если главный вектор внешних сил за рассматриваемый промежуток времени равен нулю, то количество движения механической системы постоянно. Из уравнения (4.5) следует, что если 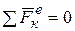 , то
, то 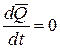 , т.е.
, т.е.
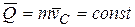 (4.7)
(4.7)
2. Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна. Например, при 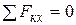 , то из (4.5)
, то из (4.5) 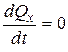 , откуда
, откуда
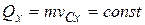 (4.7 /)
(4.7 /)
Следствия из теоремы об изменении количества движения механической системы выражают закон сохранения количества движения системы, откуда следует, что внутренние силы изменить количество движения системы не могут.
При решении задач применение теоремы позволяет исключить из рассмотрения все внутренние силы. Поэтому рассматриваемую систему надо стараться выбирать так, чтобы все (или часть) заранее неизвестных сил сделать внутренними.
Закон сохранения количества движения удобно применять в тех случаях, когда по изменению поступательной скорости одной части системы надо определить скорость другой. В частности, этот закон широко используется в теории удара, при изучении движения тела переменной массы (например, при движении ракеты).
Вопросы для самоконтроля
1. Что называется количеством движения механической системы?
2. Чему равно количество движения маховика, вращающегося вокруг неподвижной оси, проходящей через его центр тяжести?
3. Сформулируйте теоремы об изменении количества движения материальной точки и механической системы в дифференциальной и интегральной формах.
4. Выразите каждую из этих четырех теорем векторным уравнением и тремя уравнениями в проекциях на оси координат.
5. При каких условиях количество движения механической системы не изменяется? При каких условиях не изменяется его проекция на некоторую ось?
6. Могут ли внутренние силы изменить количество движения механической системы или количество движения ее части?
7. Что характеризует импульс силы?
8. Как изменяется количество движения точки, движущейся равномерно по окружности?
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 926; Нарушение авторских прав?; Мы поможем в написании вашей работы!