
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И определения
|
|
|
|
Введение в динамику. Законы динамики. Основные понятия
Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил.
Движение тел с чисто геометрической точки зрения рассматривалось в кинематике. В динамике, в отличие от кинематики, при изучении движения тел учитываются как действующие на них силы, так и инертность самих материальных точек.
В статике было введено понятие о силе, как об основной мере механического действия, оказываемого на материальное тело, но при этом не учитывалось, что сила с течением времени может изменяться. При этом переменными могут быть и силы вызывающие движение тела, и реакции связей. Переменные силы могут зависеть как от времени, так и от положения тела и от его скорости. Например, от времени зависит сила тяги электровоза при постепенном включении или выключении реостата; от положения тела зависит ньютонова сила тяготения или сила упругости пружины; от скорости зависят силы сопротивления среды.
Инертность тела проявляется в том, что оно сохраняет свое движение при отсутствии действующих сил, а если на него начинает действовать сила, то скорости точек тела изменяются не мгновенно, а постепенно и тем медленнее, чем больше инертность этого тела. Количественной мерой инертности материального тела является физическая величина, называемая массой тела.
В классической механике масса m рассматривается как величина скалярная, положительная и постоянная для каждого тела. Кроме суммарной массы движение тела зависит еще в общем случае от формы тела, т.е. от распределения массы в теле.
Простейшим объектом изучения в динамике является материальная точка – это модель тела любой формы, размерами которого в рассматриваемых задачах можно пренебречь и принять за геометрическую точку определенной массы.
Более сложные материальные объекты – механические системы и сплошные тела – считают состоящими из материальных точек. В основе динамики лежат законы, впервые сформулированные Ньютоном и названные им аксиомами или законами движения. Первый закон (закон инерции): материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние.
Закон инерции отражает одно из основных свойств материи – пребывать неизменно в движении. Систему отсчета, в которой справедлив закон инерции, называют инерциальной системой отсчета.
При решении большинства технических задач с достаточной для практики точностью, можно считать систему отсчета, связанную с Землей, инерциальной.
Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы: ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление.
Математически этот закон выражается векторным равенством
 или
или  (1.1)
(1.1)
при этом между модулями ускорения и силы имеет место зависимость
 . (1.1 /)
. (1.1 /)
Второй закон, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, поскольку при действии данной силы точка, масса которой больше, т.е. более инертная, получит меньшее ускорение и наоборот.
Если на тело действует одновременно несколько сил, то они будут эквивалентны одной силе, т.е. равнодействующей  , равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид:
, равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид:
 или
или  (1.2)
(1.2)
Третий закон (закон равенства действия и противодействия). Всякому действию соответствует равное и противоположно направленное противодействие.
Этим законом мы уже пользовались в статике. Он играет важную роль в динамике системы материальных точек, как устанавливающий зависимость между действующими на эти точки внутренними силами. При взаимодействии двух свободных материальных точек, они, согласно третьему и второму законам динамики, будут двигаться с ускорениями, обратно пропорциональными их массам.
1.2 Дифференциальные уравнения движения свободной
материальной точки
Используя основной закон динамики точки, можно вывести дифференциальные уравнения движения точки, вид которых зависит от способа задания движения точки.
Рассмотрим движение материальной точки М массой m под действием приложенных к ней сил  . Основное уравнение динамики имеет вид:
. Основное уравнение динамики имеет вид:
 . (1.3)
. (1.3)
1) При векторном способе задания движения точки  уравнение (1.3) примет вид:
уравнение (1.3) примет вид:
 . (1.3 /)
. (1.3 /)
(1.3 /) – дифференциальное уравнение движения материальной точки.
2) При координатном способе  дифференциальные уравнения движения точки имеют вид:
дифференциальные уравнения движения точки имеют вид:
 , или
, или  (1.3/ / )
(1.3/ / )
где  .
.
3) При естественном способе задания движения точки ( , где S – дуговая координата,
, где S – дуговая координата,  ) (см. «Кинематика») дифференциальные уравнения запишутся в виде:
) (см. «Кинематика») дифференциальные уравнения запишутся в виде:
 (1.3 ///)
(1.3 ///)

1.3 Задачи динамики точки и методы их решений
С помощью дифференциальных уравнений движения точки можно решать две задачи динамики точки.
Первая задача динамики. Зная массу точки m и уравнения ее движения х = f 1( t ); y = f 2( t ) и z = f 3( t ), найти модуль и направление равнодействующей сил, приложенных к точке. Эта задача легко решается следующим путем:
 ;
; 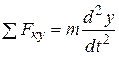 ;
;  ,
,
тогда, 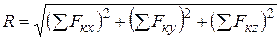 ;
;
 .
.
Пример: Уравнения движения точки М массой m имеют вид:  . Определить равнодействующую приложенных к точке сил.
. Определить равнодействующую приложенных к точке сил.
Решение: Исключая время t из уравнений движения находим уравнение траектории точки  .
.
Траектория окружности радиусом r (рис.1.1).

Рисунок 1.1.
Определяем проекции ускорения точки на оси координат:
 .
.
Находим проекции равнодействующей силы:


Определяем модуль и направление силы:
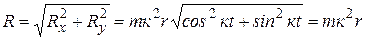

 .
.
Углы, составленные направлением силы  с направлением осей координат имеют значения
с направлением осей координат имеют значения  ; т.е в любой момент времени сила
; т.е в любой момент времени сила  направлена к началу координат О. Таким образом, установлено, что на точку действует сила притяжения, модуль которой пропорционален массе точки и ее расстоянию от центра притяжения О.
направлена к началу координат О. Таким образом, установлено, что на точку действует сила притяжения, модуль которой пропорционален массе точки и ее расстоянию от центра притяжения О.
Вторая (основная) задача динамики.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 457; Нарушение авторских прав?; Мы поможем в написании вашей работы!