Зная силы, действующие на материальную точку, ее массу m, а также начальные условия (начальное положение точки и ее начальную скорость) получить уравнение движения точки

Для решения этой задачи необходимо в левую часть уравнений (3^//) подставить значение массы m, а в правую часть – суммы проекций приложенных сил и полученные уравнения дважды проинтегрировать по времени. Эта задача имеет большое практическое значение и в общем случае является более сложной, чем первая. Так как силы, действующие на материальную точку, в общем случае является переменными величинами, то правые части дифференциальных уравнений движения могут быть функциями 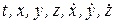, и поэтому система дифференциальных уравнений (3^//) в общем случае будет совместной.

При интегрировании каждого дифференциального уравнения движения точки появляются две постоянные, а поэтому при интегрировании трех дифференциальных уравнений движения точки будет шесть постоянных. Значения этих постоянных определяют по начальным условиям движения: значениям трех координат точки и проекциям ее скорости на три оси в некоторый момент времени, обычно (но не обязательно) в начальный момент времени.

Пусть в начальный момент времени t = t ₀ известны координаты точки и проекции ее скорости на оси, т.е.

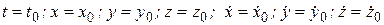(1.4)

Эти значения подставляют в уравнения, представляющие собой общие решения дифференциальных уравнений движения точки. Из этих уравнений определяют постоянные интегрирования С₁, С₂,….С₆ в зависимости от начальных координат и проекций начальной скорости. Подставляя найденные значения постоянных интегрирования в общее решение дифференциальных уравнений движения точки, получают уравнения движения точки в виде

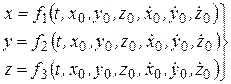. (1.5)

Уравнения (1.5) показывают, что под действием одной и той же силы материальная точка может совершать целый класс движений, определяемых начальными условиями движения.

Так, например, под действием силы тяжести материальная точка может двигаться как по вертикали, так и по семейству парабол, причем вид траектории ее движения будет зависеть от начальных условий ее движения.

Действительно, координаты движущейся точки в каждый момент времени зависят как от действующих на точку сил, так и от начального положения точки и ее начальной скорости. При составлении дифференциальных уравнений движения материальной точки за расчетный начальный момент обычно принимается момент начала движения материальной точки под действием заданных сил, для которого известны как положение точки, так и ее скорость.

Путем введения начальной скорости точки учитывается влияние на ее движение сил, действовавших на материальную точку до того момента, который принят за начальный.

Так, например, скорость вылета снаряда из орудия, принимаемая за начальную скорость его полета, учитывает результат действия на снаряд сил давления пороховых газов при движении снаряда по каналу ствола орудия до момента его вылета из орудия.

Дифференциальные уравнения движения материальной точки описывают движение точки до тех пор, пока на нее действуют силы, вошедшие в правую часть уравнений (1.3^//). Если в какой-то момент времени действие этих сил на материальную точку изменяется или прекращается, то для описания последующего движения точки надо составлять новые дифференциальные уравнения движения. Начальными условиями нового движения точки будут ее положение и скорость в конце предшествующего движения.

Вопросы для самоконтроля

1. Сформулируйте основные законы динамики.

2. Какое уравнение называется основным уравнением динамики?

3. Какова мера инертности твердых тел при поступательном движении?

4. Какую систему отсчета называют инерциальной?

5. В каком виде записываются дифференциальные уравнения движения свободной материальной точки?

6. Какие уравнения динамики называются естественными уравнениями движения материальной точки?

7. В чем заключается первая задача динамики точки и с помощью каких математических действий она решается?

8. В чем заключается вторая (основная) задача динамики точки, с помощью каких математических действий она решается?

9. Как определяются постоянные при интегрировании дифференциальных уравнений движения материальной точки?

Дата добавления: 2014-11-08