Системы. Теорема об изменении момента количества движения механической

Теорема об изменении момента количества движения механической

5.1 Моменты количества движения материальной точки относительно

центра и оси. Теоремы об изменении моментов количества движения

материальной точки относительно центра и оси

В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектора количества движения 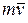рассматривают его момент относительно некоторого центра или оси. Эти моменты определяются так же, как и моменты силы (см. «Статика» (5.1^/)и (10.1)).

Таким образом, моментом количества движения точки относительно некоторого центра О называется векторная величина 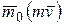, определяемая равенством

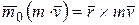, (5.1)

где r – радиус-вектор движущейся точки, проведенный из центра О.

При этом вектор 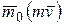направлен перпендикулярно плоскости, проходящей через 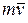и центр О (рисунок 5.1),

. (5.2)

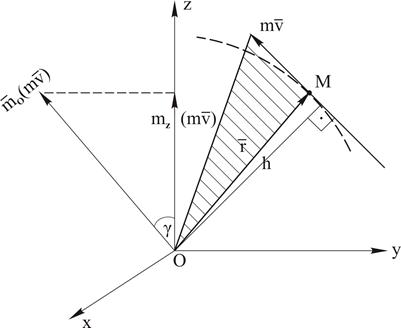
Рисунок 5.1

Момент количества движения точки относительно какой-нибудь оси Оz, проходящей через центр О, будет равен проекции вектора 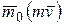на эту ось:

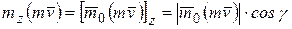(5.3)

где γ – угол между вектором 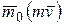и осью Оz.

Теорема об изменении момента количества движения точки (теорема моментов) устанавливает, как изменяется со временем вектор 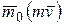. Чтобы доказать ее, продифференцируем по времени выражение (5.1). Получим

,

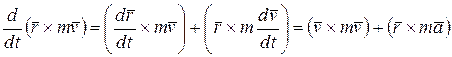но 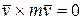как векторное произведение двух параллельных векторов, а 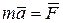, где при действии нескольких сил 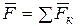, следовательно,

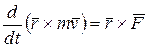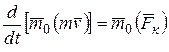или (5.4)

В результате мы доказали теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.

Если спроектировать обе части равенства (5.4) на какую-нибудь ось Оz, проходящую через центр О, то, учтя соотношение (5.3), получим

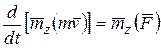(5.5)

Это равенство выражает теорему моментов относительно оси: производная по времени от момента количества движения материальной точки относительно некоторой неподвижной оси равна моменту действующей на точку силы, относительно той же оси.

Следствия:

1. Из (5.4) следует, что если 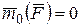, то 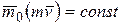, т.е. если момент действующей силы относительно некоторого центра равен нулю, то момент количества движения токи относительно того же центра есть величина постоянная. Такой результат имеет место в практически каждом случае движения под действием центральной силы.

Центральной силой называется сила, линия действия которой за время движения проходит через некоторый центр, а модуль зависит от расстояния между этим центром и точкой приложения силы.

2. Если момент силы, приложенной к материальной точке относительно некоторой оси равен нулю, то момент количества движения точки относительно этой оси остается постоянным, т.е. если 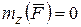, то .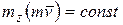

5.2 Главный момент количества движения системы

Главным моментом количеств движения (или кинетическим моментом) системы относительно данного центра О называется величина 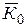, равная геометрической сумме моментов количеств движений всех точек системы относительно этого центра.

Величину 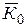для кратности часто называют кинетическим моментом или просто моментом количества движения системы.

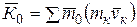, (5.6)

где 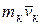- количество движения к^й материальной точки данной механjической системы.

Аналогично определяются кинетические моменты системы относительно координатных осей:

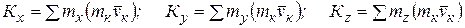(5.7)

При этом К_х, К_у, К_z, представляют собой одновременно проекции вектора 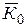на координатные оси. Кинетический момент системы может рассматриваться как характеристика ее вращательного движения (количество движения системы рассматривается как характеристика ее поступательного движения).

5.3 Кинетический момент вращающегося тела

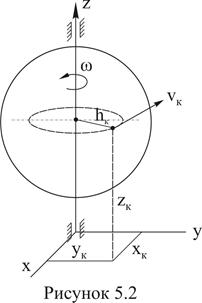
В качестве важного конкретного примера найдем значения К_z для тела, вращающегося вокруг неподвижной оси z (рисунок 5.2).

Определим кинетический момент тела относительно оси z. У любой точки тела, отстоящей от оси вращения на расстоянии 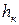, скорость v_к=ω·h_к (ω - угловая скорость тела). Следовательно, для этой точки, 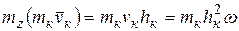тогда для всего тела, вынося общий множитель ω за скобки, получим:

,

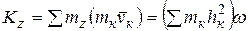где 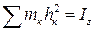- момент инерции тела относительно оси z. Окончательно находим:

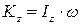. (5.8)

Таким образом, кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

Если система состоит из нескольких тел, вращающихся вокруг одной и той же оси, то

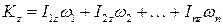. (5.9)

5.4 Теорема об изменении кинетического момента системы

Теорема моментов, доказанная для одной материальной точки будет справедлива для каждой из точек системы. Следовательно, если мы рассмотрим механическую систему состоящую из n точек, на каждую из которых действуют внешние и внутренние силы, то для к^й точки системы, имеющей скорость 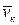, можно записать:

,

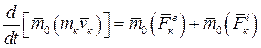где 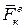и 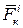- равнодействующие всех внешних и внутренних сил, действующих на каждую точку.

Составляя такие уравнения для всех точек системы и складывая их почленно, получим:

.

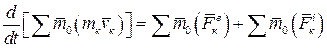Но последняя сумма по свойству внутренних сил системы равна нулю. Тогда, учитывая равенство (5.6) получим окончательно:

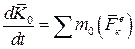, (5.10)

где 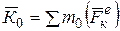- главный момент количества движения системы.

Полученное уравнение выражает следующую теорему моментов в дифференциальной форме для системы: производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра. Проецируя обе части равенства (5.10) на неподвижные оси Охуz, получим:

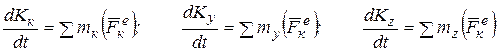. (5.11)

Уравнение (5.11) выражает теорему моментов в дифференциальной форме относительно любой неподвижной оси.

Практическая ценность теоремы моментов состоит в том, что она, аналогично теореме об изменении количества движения, позволяет при изучении вращательного движения системы исключать из рассмотрения все наперед неизвестные внутренние силы. Из теоремы моментов можно получить такие следствия:

1. Если сумма моментов относительно центра О всех внешних сил, действующих на систему, равна нулю 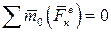, то 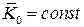. Таким образом, если сумма моментов относительно данного центра всех приложенных к системе внешних сил равна нулю, то главный момент количеств движения системы (кинетический момент системы) относительно этого центра остается постоянным.

2. Если главный момент внешних сил относительно некоторой оси остается все время равным нулю, то кинетический момент механической системы относительно этой оси остается постоянным. Например, если 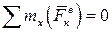, то 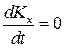, т.е. 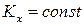. Следствия из теоремы об изменении кинетического момента механической системы выражают закон сохранения кинетического момента механической системы. Из них следует, что внутренние силы изменить главный момент количеств движения системы не могут.

Дата добавления: 2014-11-08