Нестабильность затрат времени на выполнение процессов

Как было отмечено, временные связи при реализации производ­ственного процесса проявляются в виде реализации организационно- управленческих и технологических событий во времени. Длитель­ность каждого такого события можно рассматривать как случайное число. Основными числовыми характеристиками случайного числа являются математическое ожидание (номинал) и среднеквадратичес- кое отклонение. Если временная связь реализуется в виде последова­тельности несовместимых событий (С₁₍ С₂, ….., С„), то длительность процесса, реализуемого этими событиями, будет определяться по формуле

где t_c — длительность объединенного события С = t. — длительность события С=C₁UC₂U…UC_n,.

В случае независимости событий С можно определить числовые характеристики объединенного события на основе известных теорем теории вероятностей.

Теорема 1. Математическое ожидание суммы независимых случай­ных чисел равно сумме математических ожиданий составляющих случайных чисел.

Теорема 2. Дисперсия суммы независимых случайных чисел равна сумме дисперсий составляющих случайных чисел.

На основе этих двух теорем и формулы (3.8) можно записать

где M[t_c ] — математическое ожидание длительности события С,; D[t_c \ — дисперсия длительности события C_t.

Нестабильность длительности составляющих событий обусловлена следующими факторами: нестабильностью организационных мероприятий; нестабильностью выходных параметров источников энергии И т.д.

Остановимся на вопросе оценки нестабильности временных связей под действием перечисленных факторов. Значимость фактора нестабильности выходных параметров источников энергии по сравнению с другими факторами мала. Поэтому его влияние можно уменьшить путем стабилизации параметров источников энергии.

Нестабильность (потери) организационных мероприятий, влияющая на загрузку оборудования, минимизируется благодаря оптимиза­ции составления расписания работы участка с учетом маршрута и трудоемкости обработки заготовок.

Вопрос оценки надежности отдельных элементов системы необхо­димо рассматривать для нестационарных и стационарных расписаний работы системы. Стационарным расписанием называют такую организацию работы системы, при которой работа отдельных ГПМ циклически повторяется за планируемый период Т_п. Такая организация работы осуществляется обычно в средне- и крупносерийном производстве. Такое определение стационарного расписания позволяет харак­теризовать производственный процесс математическим ожиданием длительности цикла повторения. Такой подход широко используют при анализе производительности автоматических и поточных линий. Временная диаграмма такой организации производственного процесса показана на рис. 3.7, а, определение математического ожидания длительности цикла повторения стационарных расписаний базируется на теории восстановления.

Нестационарным расписанием называют такую организацию работы системы, при которой за планируемый период работа отдельных ГПМ циклически не повторяется (рис. 3.7, б). Анализ работы такого участка основан на теории невосстанавливаемых систем.

Для анализа производственного процесса с нестационарным расписанием задача ставится следующим образом: для обеспечения задан-

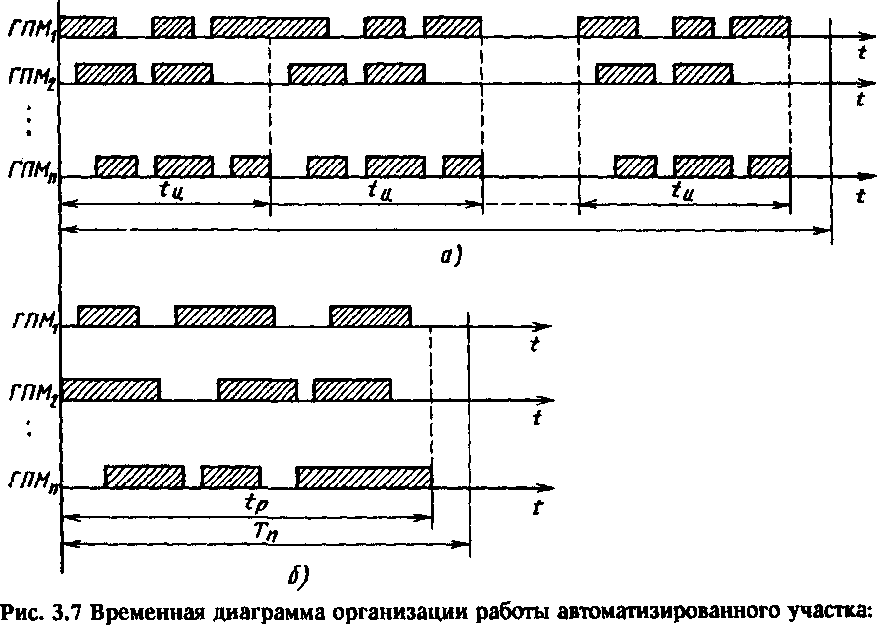а — стационарное расписание; б — нестационарное расписание; t_u — длительность цикла повторения

ного уровня вероятности PU_p) выполнения расписания необходимо определить уровень надежности отдельных элементов системы Pj(t_c).

Если временная связь работы отдельных элементов (ГПМ) опреде­ляется по (3.7), то можно записать Я_{гпм с}(*_р) £ P(t_p), ГДеР_{ГПМ с}«_р)

— вероятность того, что i-й ГПМ не откажет в течение времени t_p (длительность работы ГПМ за планируемый период).

Если за время t_р для i-й ГПМ реализуется п несовместимых собы­тий, каждое длительностью tp то можно записать

где Р_сi (t_i) — вероятность реализации события C_i за время t_i.

Из (3.9) можно определить вероятность реализации событий С,- только при допущении о том, что эти события равновероятны, т.е. при Р_c1 (t₁;) = Р_с2 (t₂) =... = Р_с (t_n) = Р. При таком допущении согласно

Исходя из известного значения Р и конкретного закона распреде­ления длительности отдельных событий С,-, можно добиться, чтобы условие (3.9) было удовлетворено и тем самым решить поставленную задачу.

3.4. Надежность процессов и оборудования

Основные термины и понятия теории надежности

Безотказность — свойство устройства сохранять работоспособ­ность в течение заданного интервала времени при определенных условиях эксплуатации.

Вероятность отказа — вероятность того, что в течение заданного интервала времени работы при определенных условиях эксплуатации возникнет хотя бы один отказ устройства.

Внезапный отказ — отказ, возникший в результате скачкообраз­ного изменения значений одного или нескольких основных парамет­ров устройства.

Восстанавливаемое устройство — устройство, работа которого после отказа может быть возобновлена в результате проведения необходимых восстановительных работ.

Время восстановления — продолжительность перерыва в работе восстанавливаемого устройства при устранении отказа.

Время безотказной работы — время, в течение которого устрой­ство, выполняя свои функции, безотказно работает.

Наработка до отказа — случайный интервал времени с момента окончания очередного восстановления и начала работы устройства до следующего отказа.

Интенсивность восстановления — условная плотность вероятнос­ти восстановления в некоторый момент при условии, что к этому моменту устройство не восстановлено.

Интенсивность отказов — условная плотность вероятности отказа устройства в некоторый момент времени при условии, что до этого момента отказа не было.

Коэффициент готовности — вероятность того, что восстанавлива­емое устройство будет работоспособно в любой, произвольно выбран­ный момент времени в стационарном процессе функционирования.

Математическое определение основных показателей надежности

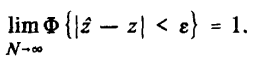В данном подразделе для всех показателей надежности приведены два определения — вероятностное и статистическое. Через z обозна­чен статистический показатель, соответствующий аналогичному показателю z. При этом имеется в виду, что по закону больших чисел теории вероятностей всякое выборочное среднее с увеличением числа опытов N сходится к математическому ожиданию соответствующей случайной величины, т.е. для всякого сколь угодно малого е выпо­лняется условие

Рассмотрим основные показатели надежности.

1. Вероятность безотказной работы устройства в интервале време­ни от 0 до t₀.

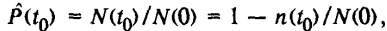
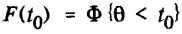
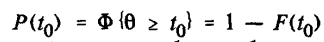Вероятностное определение: где P(t₀) — вероятность того, что устройство проработает безотказно в течение требуемого интервала времени t₀, начав работать в момент времени t = 0, или вероятность того, что случайное время работы устройства до отказа окажется больше требуемого интервала времени работы; θ — случайное время безотказной работы устройства до появления отказа; — функция распределения слу­чайной величины θ.

Статистическое определение: где N(t₀) — число реализаций, для которых время безотказной работы устройства больше t₀; n(t₀) — число реализаций, для которых время безотказной работы устройства меньше t₀; n(t₀) — общее число реали­заций безотказной работы устройства.

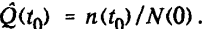
2. 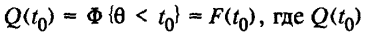Вероятность отказа устройства в интервале времени от 0 до t₀. Вероятностное определение: вероятность того, что устройство откажет в течение требуемого интервала времени начав работать в момент времени t = 0, или вероятность того, что случайное время работы устройства до отказа окажется меньше требуемого интервала времени безотказной работы t₀.

Статистическое определение (рис. 3.8):

3. 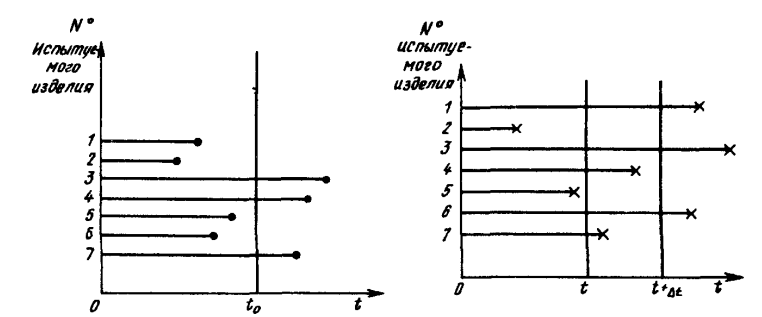Частота отказов (плотность распределения F(t)) устройства в момент времени t.

Рис.3.8. Временная диаграмма испытаний Рис.3.9. Временная диаграмма испытаний

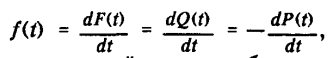Вероятное определение:, где f(t) — плотность вероятности того, что случайное время безотказной работы устройства окажется меньше t, или плотность вероятности отказа для момента времени t.

Статистическое определение (рис. 3.9):, где n(t+Δt) — число

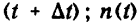устройств, отказавших до момента - число устройств, отказавших до момента t.

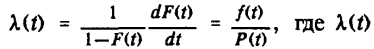4. Интенсивность отказов устройства в момент времени t.

Вероятностное определение: - условная

плотность вероятности отказа устройства для момента времени t при условии, что до момента времени t отказа устройства не произошло.

Используя вероятностное определение частоты отказов, получим

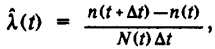
Статистическое определение (рис. 3.9) где N(t) — число

неотказавших устройств до момента t.

5. Интенсивность восстановления устройства в момент времени t, отсчитывемый от момента начала восстановления.

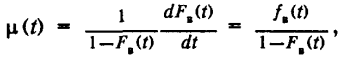
Вероятностное определение: --------------------------------------------------- где μ(t) —

плотность условной вероятности восстановления устройства.

для момента времени t, отсчитываемого от момента начала восстанов­ления при условии, что до момента времени i восстановление устрой­ства не произошло;

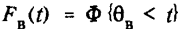— функция распределения случайного времени восстановления

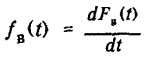
устройства; - плотность распределения F_B(t).

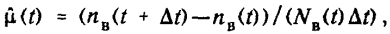
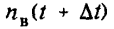Статистическое определение: где

— число восстановившихся устройств до момента (t + Δt); n_B(t) — число восстановившихся устройств до момента t; N_B(t) — число невосстановившихся устройств до момента t.

6. Коэффициент готовности устройства μ.

Для любых распределений времени между отказами F(t) и време­ни восстановления F_B(t), имеющих конечные средние значения соот­ветственно Т и τ, всегда выполняется следующее соотношение: η = Т/(Т + τ).

Структурные компоновки автоматических линий

Автоматическая линия (AJI) — это система машин (комплекс основного и вспомогательного оборудования), автоматически выпо­лняющая в определенной технологической последовательности и с заданным ритмом весь процесс изготовления или переработки продук­ции производства. По структурной компоновке различают следующие AJI: однопоточные синхронного действия (рис. 3.10, а); двухучастковые однопоточные асинхронного действия (ОД AJI) (рис. 3.10, б); однопоточные асинхронного действия (рис. 3.10, в); многопоточные многоучастковые асинхронного действия без накопителей (рис. 3.10, г); многопоточные многоучастковые AJI асинхронного действия с накопителями (рис. 3.10, д).

Проектная производительность AJI: Q_np = Q_kή_л, где Q_k — номи­нальная производительность выпускающего участка; ή_л — коэффици­ент готовности AJI.

Существующие расчетные методы определения коэффициента готовности AJI основаны на использовании в качестве исходных данных характеристик надежности встроенного оборудования. Анализ структурных компоновок AЛ показывает, что в качестве участка или потока могут быть использованы или отдельный станок, или же АЛ синхронного действия. В теории производительности каждый элемент характеризуется следующими основными параметрами надежности:

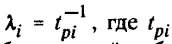
интенсивностью потока отказов где t_pi — среднее время безотказной работы i-гo элемента;

интенсивностью потока восста­новлений — сред­нее время

восстановления i-го элемента;

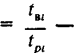
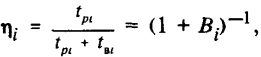коэффициентом готовности, определяющим конструктивное совершенство i-го элемента, где B_i внецикловые потери,

предоставляющие собой простой, при­ходящиеся на единицу времени безотказной работы элемента.

Рис.3.10 – Компоновка АЛ

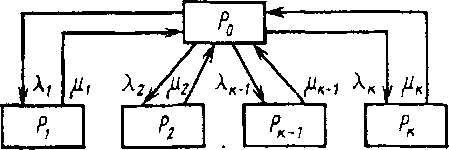
Определим коэффициент готовности AJI синхронного действия (см. рис. 3.10, а). В АЛ синхронного действия отказ любого агрегата приводит к отказу всей системы, поэтому число возможных состоянии будет равно к + 1. Следовательно: 1-е состояние — все элементы системы работают (вероятность этого состояния Р₀); 2-е состояние — 1-й элемент системы отказал, а остальные элементы работоспособны (вероятность этого состояния к-е состояние — (к — 1)-й элемент системы отказал, а остальные элементы работоспособны (вероятность этого состояния Р_к-1); (к + 1) - е состояние — к-й элемент системы отказал, а остальные элементы работоспособны (вероятность этого состояния P_k.

Ориентированный граф состояний AJI синхронного действия пока­зан на рис. 3.11. На основании графа получают следующую систему уравнений для определения вероятностей состояний:

Рис. 3.11. Ориентированный граф состояний АЛ синхронного действия

(3.10)

При этом выполняется следущее нормирующее условие: С его учетом решение системы уравнение (3.10) запишется в виде:

(3.11)

При этом интенсивность потока отказов и интенсивность потока восстановления АЛ синхронного действия соответственно можно вычислить по следующим формулам: где - коэффициент готовности АЛ
[вычисляется по формуле (3.11)]; 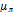- интенсивность восстановления АЛ; 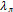- интенсивность отказа АЛ.

Метод расчета надежности и производительности однопоточных АЛ с накопителями

Рассмотрим алгоритм получения нижней оценки коэффициента готовности однопоточной AJI. С этой целью проанализируем, как функционирует трехучастковая AJ1 (рис. 3.12, а).

На рис. 3.12 приняты следующие обозначения: 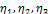— соот­ветственно собственные коэффициенты готовности 1, 2 и 3-го учас­тков; B₁, В₂, В₃ — соответственно удельные потери 1, 2 и 3-го участков; 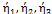, Пз — соответственно коэффициенты готовности 1, 2 и 3-го участков в составе AJI.

Как известно, в рассматриваемой AJI коэффициент готовности линии будет равен коэффициенту готовности 3-го участка АЛ. Допустим, что в рассматриваемой ли­нии 1-й участок отсутствует или надежность этого участка равна единице. В этом случае коэффи­циент готовности рассматривае­мой линии будет равен коэффи­циенту готовности двухучастковой линии, состоящей из 2-го и 3-го участков 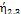(рис. 3.12, б).

Рис. 3.12. Пример получения нижней и верхней оценок коэффициента готов­ности однопоточных

Можно записать, что η_л < η_2,3, так как в этом случае мы не учли потери, которые в реаль­ной системе передаются с 1-го участка на 2-й. В этом случае фонд времени 3-го участка на единицу времени работы.

(3,12)

В действительности, для получения искомого значения коэффици­ента готовности всей линии нужно уменьшить надежность 2-го учас­тка таким образом, чтобы фонд времени 3-го участка на единицу времени работы был равен искомому (рис. 3.12, в), т.е.

(3,13)

Сравнив (3.12) и (3.13), получим, что. Это объяс­няется тем, что надежность 3-го участка осталась прежней, а надеж­ность 2-го участка стала меньше, в результате выросла вероятность простоя 3-го участка по вине 2-го участка. Для определения оценки В₂ рассмотрим линию из 1-го и 2-го участков без учета влияния 3-го участка или надежность 3-го участка примем равной единице. В этом случае (рис. 3.12, г) фонд времени 2-го участка на единицу времени его работы

(3.14)

В исходной системе, когда надежность 3-го участка меньше едини­цы, коэффициент наложения потерь δ_1,2 будет меньше, так как это равносильно тому, что надежность 2-го участка будет несколько меньше, чем η₂. Поэтому влияние 1-го участка на 2-й участок умень­шается, что равносильно уменьшению коэффициента наложения потерь. Следовательно, в исходной системе доля потерь 1-го учас­тка, передаваемых на 2-й участок будет меньше, чем δ_1,2 B ₁ [см. (3.14)]. Тогда

Теперь в исходной линии 1-й и 2-й участки заменим участком с коэффициентом готовности

Структура такой АЛ приведена на рис. 3.12, д. Для полученной структуры фонд времени 3-го участка на единицу времени его работы

Можно утверждать, что, так как

Следовательно, или

На основании полученного результата можно разработать алго­ритм расчета нижней оценки коэффициента готовности для однопо- точной структуры АЛ с накопителями (рис. 3.13, а). Предлагаемый метод заключается в следующем. Из всей структуры АЛ выделим 1-й и 2-й участки и вычислим коэффициент готовности этой двухучастковой АЛ. Коэффициент готовности (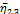) узла, состоящего из 1-го и 2-го участков, на основании сделанного вывода о действии наложен­ных потерь будет меньше, чем коэффициент готовности этого же узла в составе АЛ ().

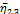Теперь в исходной структуре 1-й и 2-й участки заменим одним участком с коэффициентом готовности (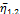) и объединим с 3-м учас­тком. Для полученной двухучастковой AJI вычислим коэффициент готовности (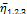) который заведомо будет меньше, чем коэффициент готовности узла (состоящего из 1, 2 и 3-го участков) в системе 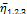. Далее 1, 2 и 3-й участки заменим одним участком с коэффициентом готовности 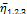и объединим его с 4-м участком. Для полученной двухучастковой AJI вычислим коэффициент готовности 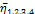который будет меньше, чем коэффициент готовности этого узла в составе AJI. Если этот процесс продолжить до последнего участка, то в итоге получим нижнюю оценку коэффициента готовности 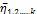. Схема определения 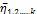показана на рис. 3.13, б.

Одним из основных моментов в предложенном методе расчета нижней оценки коэффициента готовности АЛ является определение характеристик надежности объединенного (эквивалентного) участка; интенсивности остановки 𝜆_э, интенсивности окончания остановки μ_э и номинальной производительности q_э, Номинальная производитель­ность эквивалентного участка, естественно, равна производительности выпускающего (последнего) из объединенных участков, т.е. q_э = q_i при объединении i участков.

Рис.3.13. Схема алгоритма расчет нижней ойенки коэффициента готовности АЛ

Для определения интенсивности отказов и восстановлений эквива­лентного участка воспользуемся решением для коэффициента готов­ности двухучастковой АЛ и ориентированным графом состояний. Так как случайный процесс функционирования двухучастковых АЛ является эргодическим, то среднее время пребывания в каждом состоянии будет равняться обратной величине суммарной интенсив­ности ухода из этого состояния. Поэтому на основании ориентирован­ного графа состояний и по известным значениям вероятности пребы­вания в каждом состоянии можно определить среднее время работы между двумя остановами однопоточной двухучастковой АЛ (ОДАЛ). На основании ориентированного графа состояний двухучастковой АЛ среднее время работы до отказа и среднее время восстановления будут вычисляться соответственно по следующим формулам:

(3,15)

где а_j - возможное состояние AJI; 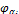— суммарная интенсивность выхода из состояния α_j; 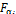(z) — вероятность того, что AJI находит­ся в состоянии{ α_j; z}; ⁼ 0, если в α_j -м состоянии АЛ простаива­ет; = 1, если в вум состоянии АЛ работает; 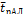— среднее время восстановления ОДАЛ; η_л — коэффициент готовности ОД АЛ;

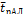— среднее время между простоями ОДАЛ.

На основании формулы (3.15) эквивалентные параметры объеди­ненного (эквивалентного) участка будут вычисляться по следующей формуле:

Структурная схема алгоритма, реализующая изложенный метод, приведена на рис. 3.14.

В качестве примера на рис. 3.15 показан ориентированный граф состояний для двухучастковой АЛ с равными производительностями участков. Значения параметров

приведены в табл.3,1. Как следует из таблицы,

Где - вероятности пребываниря АЛ в состояниях

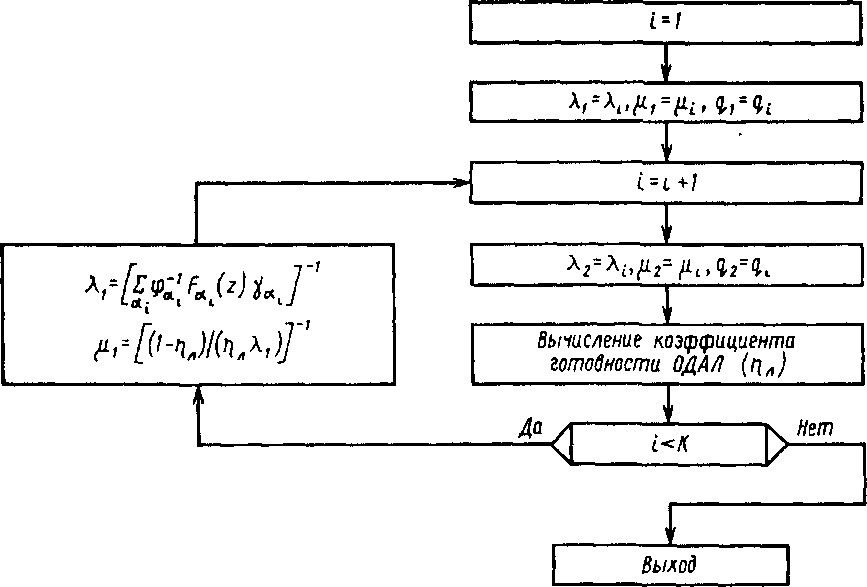Рис. 3.14. Структурная схема алгоритма вычисления нижней оценки коэффициента готовности AJI

Рис. 3.15. Ориентированный граф состояний двухучастковой АЛ с равными произво- дительностями участков

Таким образом, получены формулы, необходимые для расчета нижней оценки коэффициента готовности однопоточной многоучас­тковой AJI с накопителями.

Теперь определим верхнюю оценку проектной производительности AJI с однопоточной структурой. Для этого проанализируем работу трехучастковой линии (см. рис. 3.12). Допустим, что в рассматривав- мой линии 3-й участок отсутствует (см. рис. 3.12, г). В этом случае на основании формулы (3.14) можно записать,

(3,16)

3.1. Функциональные зависимости для определения длительности состояний

Производительность 2-го участка с учетом (3.16) в этом случае с будет вычисляться по формуле:, где q₂ - номинальная производительность 2-го участка.

В реальной системе вследствие дополнительных потерь по вине 3-го участка

(3,17)

где ή₂ — коэффициент готовности 2-го участка в составе исход­ной АЛ.

На основании (3.17) можно записать производительность 2-го участка исходной AJI.

Теперь допустим, что в рассматриваемой системе 1-й участок отсутствует (см. рис. 3.12, б). Тогда производительность 3-го участка исходной АЛ, 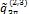— производительность 3-го участка, когда 1-й участок не влияет на работу 2-го и 3-го участков.

Производительность исходной линии

(3.18)

где q_л — производительность АЛ, η_л — коэффициент готовности АЛ.

Так как в АЛ отсутствует отбор изделий по ходу обработки, т.е. все детали проходят через всю АЛ, то действительные производитель­ности участков выравниваются. Поэтому

(3.19)

где — производительность i -го участка АЛ.

Для рассматриваемого примера с учетом (3.19) можно утверждать, что производительность АЛ не может быть больше, чем меньшая из производительностей

(3.20)

Используя (3.18) и (3.20), получим, что коэффициент готовности рассматриваемой АЛ

(3.21)

Формулу (3.21) можно применять для однопоточных АЛ с произ­вольным числом участков. В этом случае коэффициент готовности АЛ с произвольным числом участков q_k — номинальная производительность k - го (выпускающе­го) участка; q^i-1,i производительность i -го участка двухучастковой АЛ, состоящего из (i — 1)-го и i -гo участков исходной линии.

Структурная схема алгоритма вычисления верхней оценки коэф­фициента готовности АЛ с произвольным числом участков приведена на рис. 3.16.

Необходимо отметить, что при расчете нижней и верхней оценок коэффициента готовности многоучастковой АЛ необходимо уметь рассчитывать коэффициент го­товности трех вариантов двуху- частковых АЛ: когда участки с равными производительностя- ми; когда производительность 1-го участка больше, чем 2-го участка; когда производитель­ность 1-го участка меньше, чем 2 –го участка.

Рис. 3.16. Структурная схема алгоритма вычисления верхней оценки коэффици­ента АЛ

Граф состояний этих АЛ при­веден на рис. 3.15, 3.17 и 3.18, а формулы для расчета коэффици­ента готовности и вероятностей состояний приведены ниже.

Ч*')»

При расчете коэффициента готовности двухучастковых АЛ приняты обозначения: F₁₁₁ (z) — вероятность состояния, когда 1-й и 2 - й участки, а также накопи­тель находятся в работоспособ­ном состоянии, а запас заготовок в накопителе находится на про­межуточном уровне; F₁₀₁(z) — вероятность состояния, когда 1-й участок и накопитель находятся в работоспособном состоянии, 2 - й участок отказал, а запас заготовок в накопителе находит­ся на промежуточном уровне; F₀₁₁(z) — вероятность состояния, когда 2-й участок и накопитель находятся в работоспособном состоянии, 1-й участок отказал, а запас заготовок в накопителе находится на промежуточном уровне; F₁₁₀ (z) — вероятность состояния, когда 1-й и 2-й участки находятся в

работоспособном состоянии, накопитель отказал, а запас заготовок в накопителе находится на промежуточном уровне; F_Q1Q(z) — вероят­ность состояния, когда 1-й участок и накопитель отказали, 2-й учас­ток находится в работоспособном состоянии, а запас заготовок в накопителе находится на промежуточном уровне; F₁₀₀(z) — вероят­ность состояния, когда 2-й участок и накопитель отказали, 1-й участок находится в работоспособном состоянии, а запас заготовок в накопителе находится на промежуточном уровне; F₁₁₁(0) — вероят­ность состояния, когда 1-й и 2-й участки, а также накопитель нахо­дятся в работоспособном состоянии и накопитель пуст; F₁₁₀(0)— вероятность состояния, когда 1-й и 2-й участки работоспособны, накопитель отказал и он пуст; F₀₁₁(z_m)— вероятность состояния, когда 2-й участок и накопитель находятся в работоспособном состоянии, 1-й участок отказал и накопитель пуст F₁₁₁(z_m)— вероятность состоя­ния, когда 1-й и 2-й участки, а также накопитель находятся в рабо­тоспособном состоянии и накопитель полон; F₁₁₀(z_m)— вероятность состояния, когда 1-й и 2-й участки находятся в работоспособном состоянии, накопитель отказал и он полон; F₁₀₁ (z_m) — вероятность состояния, когда 1-й участок и накопитель находятся в работоспособ­ном состоянии, 2-й участок отказал и накопитель полон; z_m — вместимость накопителя; q₁, q₂ - цикловая производительность соответ­ственно 1-го и 2-го участков; τ₁, τ₂ — длительность цикла действия соответственно 1-го и 2-го участков; 𝜆₁, 𝜆₂, 𝜆₃ — интенсивность отказа соответственно 1-го, 2-го участков и накопителя; μ₁, μ₂, μ₃ интенсивность восстановления соответственно 1-го, 2-го участков и накопителя; η — коэффициент готовности двухучастковой AJI.

Коэффициент готовности двухучастковой АЛ с равными цикловы­ми производительностями участков

Вероятности возможных состояний АЛ рассчитывают по формулам:

где величины вычисляются по следующим формулам:

Коэффициент готовности двухучастковой AJI с большей цикловой производительностью 1-го участка

Вероятности возможных состоянии AJI рассчитывают по формулам:

Величины С₁, G₁, G₂ …, G₁₁ вычисляются по формуле:

Коэффициент готовности двухучастковой АЛ с большей цикловой производи - тельностью 2-го участка

Вероятности возможных состояний АЛ рассчитывают по формулам:

Величины C₁, G₁, G₂,..., G₁₁ вычисляют по следующим формулам:

Дата добавления: 2014-11-18