Площини окремого положення

Площини загального положення

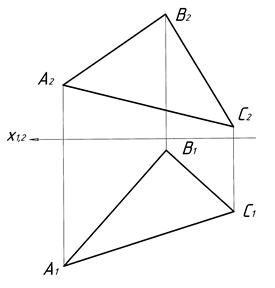
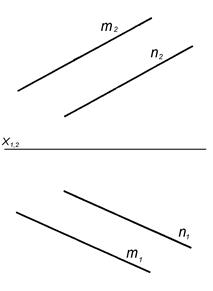
Площиною загального положення називається площина, яка не паралельна (не перпендикулярна) ні одній з площин проекцій. На рисунку 3.1 наведено приклад площини загального положення, яка задана слідами. На рисунку 3.2, а площина загального положення задана трикутником, на рисунку 3.2, б площина задана паралельними прямими.

а)	б)
Рисунок 3.2

До площин окремого положення відносяться площини рівня і проекціювальні площини.

3.2.1 Площини рівня

Площини рівня – це площини, які паралельні одній з площин проекцій.

1. Площина паралельна П₁ називається горизонтальною. Горизонтальна площина в системі площин проекцій П₁ / П₂ відображається на П₂ в пряму лінію, паралельну осі Ох. На П₁ має натуральну величину (рис.3.3).

2. Площина паралельна П₂ називається фронтальною. Фронтальна площина в системі площин проекцій П₁ / П₂ відображається на П₁ в пряму лінію, паралельну осі Ох. На П₂ має натуральну величину(рис.3.4).

3. Площина паралельна П₃ називається профільною. Профільна площина відображається на П₁ і П₂ в прямі лінії, які паралельні осям Оу і Оz. На П₃ має натуральну величину(рис. 3.5).

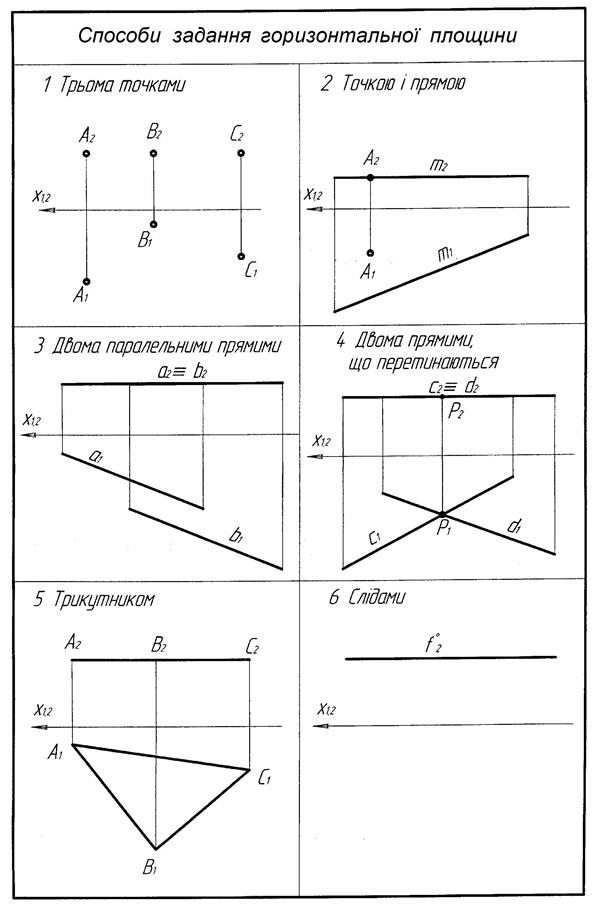
Рисунок 3.3

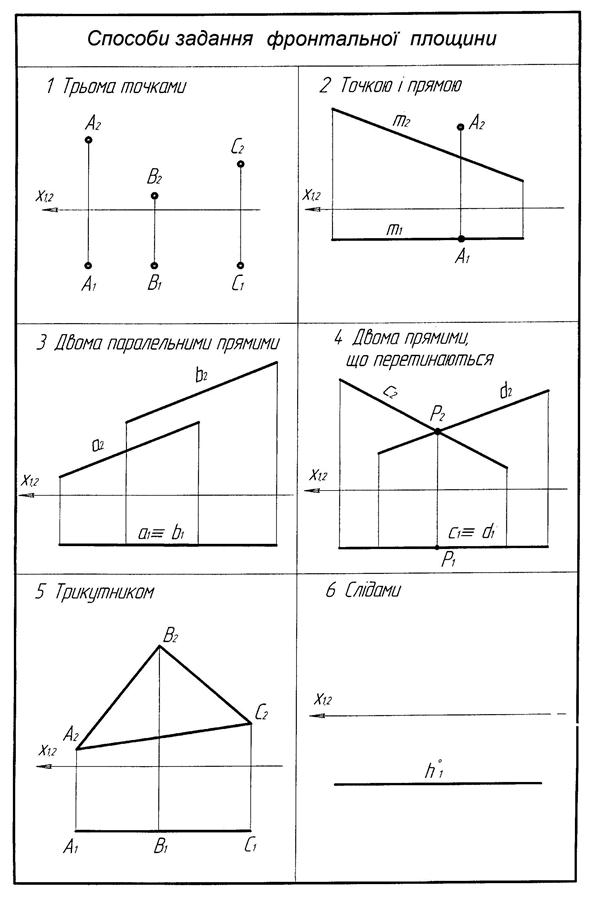
Рисунок 3.4

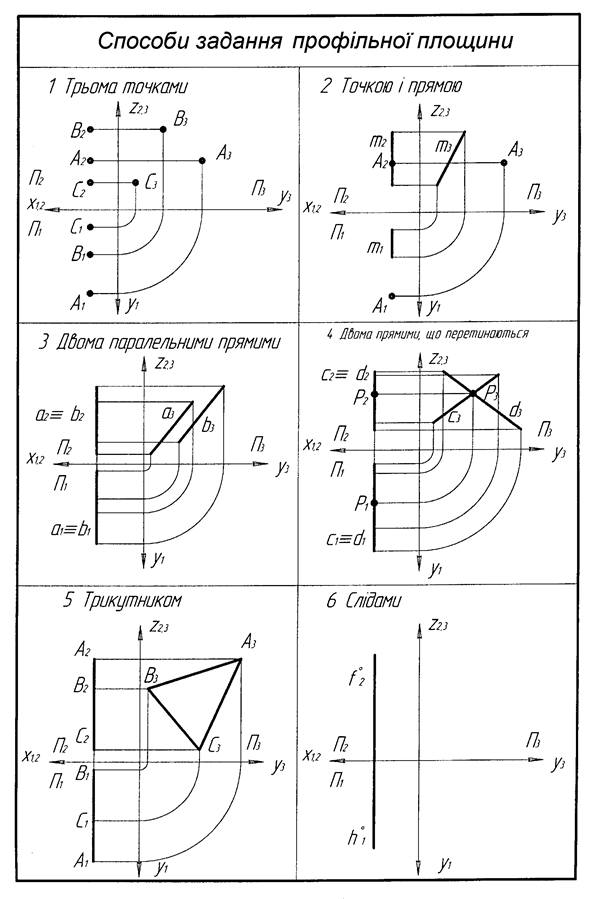
Рисунок 3.5

3.2.2 Проекціювальні площини

Проекціювальні – це площини, що перпендикулярні до однієї з площин проекцій.

1. Площина перпендикулярна до П₁ називається горизонтально-проекціювальною. Така площина відображається на П₁ в пряму лінію і має реальні кути нахилу до П₂ і П₃ (рис. 3.6).

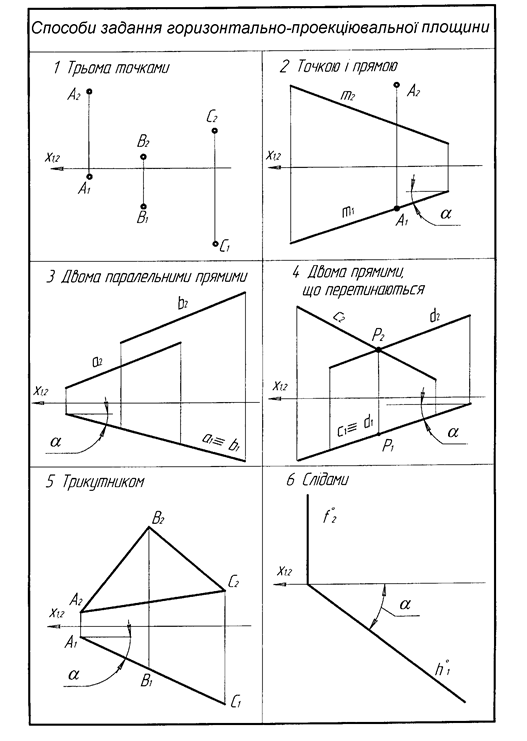
Рисунок 3.6

2. Площина перпендикулярна до П₂ називається фронтально-проекціювальною. Така площина відображається на П ₂ в пряму лінію і має реальні кути нахилу до П₁ і П₃ (рис. 3.7).

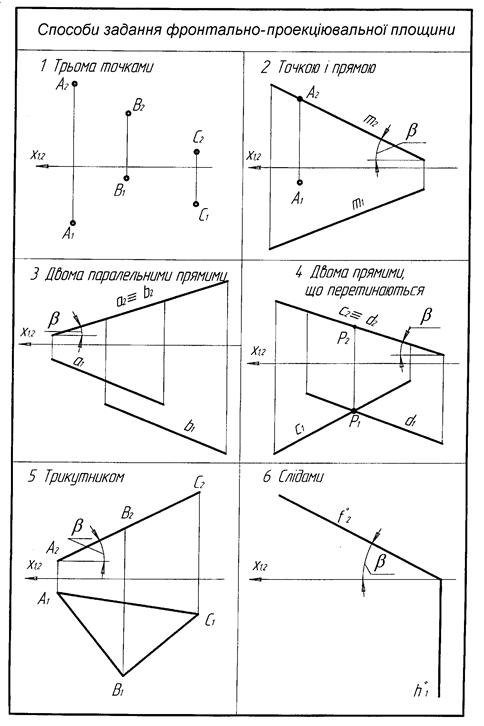
Рисунок 3.7

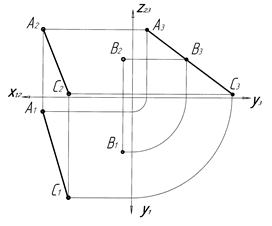
3. Площина перпендикулярна до П₃ називається профільно-проекціювальною. Така площина відображається на П₃ в пряму лінію і має реальні кути нахилу до П₁ і П₂ (рис. 3.8).

Способи задання профільно-проекціювальної площини
1 Трьома точками	2 Точкою і прямою
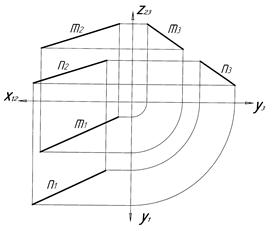
3 Двома паралельними прямими	4 Двома прямими, що перетинаються
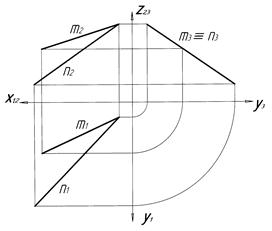
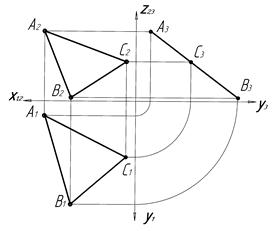
5 Трикутником	6 Слідами

Рисунок 3.8

Запитання для самоконтролю

1. Яка площина називається площиною загального положення?

2. Які площини називаються площинами рівня?

3. Які площини називаються проекціювальними?

4. Як називаються лінії перетину площини з площинами проекцій?

4 Позиційні задачі

У нарисній геометрії розглядають дві групи задач: позиційні та метричні. Групу позиційних задач складають задачі: 1) на взаємний порядок геометричних фігур; 2) на взаємну належність геометричних фігур; 3) на взаємний перетин геометричних фігур.

4.1 Точка і пряма, що належать площині

Точка належить площині, якщо вона знаходиться на прямій, яка належить даній площині. Пряма належить площині, якщо вона проходить через дві точки, що належать площині.

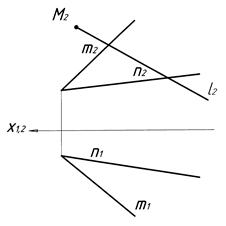
Задача. Умова: Побудувати горизонтальну проекцію точки М, що належить площині a (m Ç n). Графічну умову показано на рисунку 4.1.

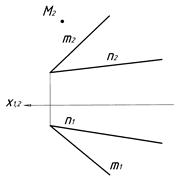
	M (M2) Ì a (m Ç n) M1 -?
Рисунок 4.1

Алгоритм розв’язання задачі

1. Через точку М (М₂) проводять пряму l (l₂), що належить заданій площині a (m Ç n) (рис. 4.2).

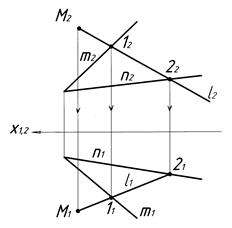
2. Визначають точки перетину прямої l з прямими m і n і будують горизонтальну проекцію прямої l (рис. 4.3). Будують горизонтальну проекцію точки М₁ на l₁.

Рисунок 4.2	Рисунок 4.3

4.2 Прямі рівня площини загального положення

Горизонталь площини це пряма, яка належить площині і паралельна горизонтальній площині проекції П₁. Побудову горизонталі наведено на рисунках 4.4–4.7. В площині загального положення, яка задана трикутником a (D АВС) (рис. 4.4), проводять фронтальну проекцію горизонталі h₂ (рис. 4.5). На фронтальній площині проекції П₂ проекція горизонталі h₂ завжди паралельна осі х_1.2. Визначають точку перетину горизонталі зі стороною ВС: h₂ Ç В₂ С₂ = 1₂ (рис. 4.6). Точку 1 проекціюють на П₁, з’єднують з вершиною трикутника А₁ і отримують горизонтальну проекцію горизонталі h₁ (рис. 4.7).

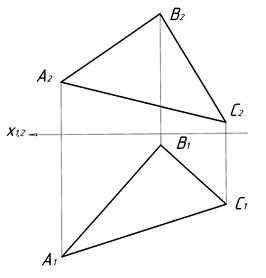Рисунок 4.4	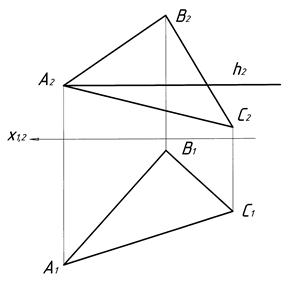Рисунок 4.5
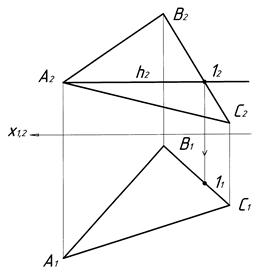Рисунок 4.6	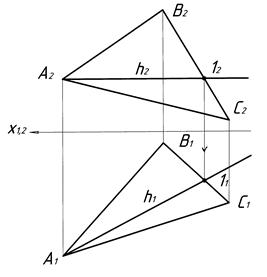Рисунок 4.7

Фронталь площини це пряма, яка належить площині і паралельна фронтальній площині проекції П₂. Приклад побудови фронталі площини наведено на рисунку 4.8. Побудову фронталі починають на горизонтальній площині проекції. Горизонтальну проекцію фронталі f₁ проводять в площині b (m ½½ n) паралельно осі х_1,2. Визначають точки перетину f₁ з горизонтальними проекціями прямих m₁ і n₁: f₁ Ç m₁ = 1₁, f₁ Ç n₁ = 2₁. Ці точки 1 і 2 проекціюють на П₂, з’єднують і отримають фронтальну проекцію фронталі площини f₂.

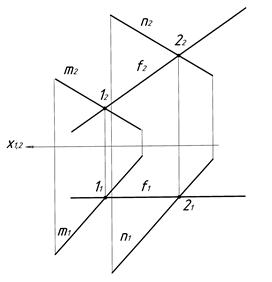
Рисунок 4.8

4.3 Перетин прямої з площиною загального положення. Перша

позиційна задача

Ця задача – одна з основних задач нарисної геометрії.

Алгоритм розв’язання задачі

1. Через задану пряму проводять допоміжну площину окремого положення.

2. Будують лінію перетину двох площин – заданої і допоміжної.

3. Визначають точку перетину прямої з площиною.

4. Визначають видимість прямої відносно площини за допомогою конкуруючих точок.

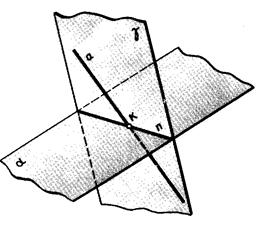
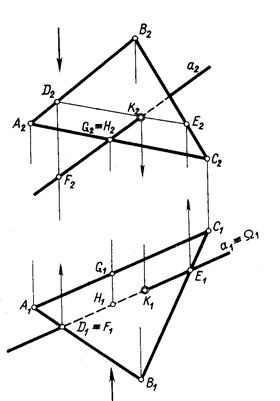
На рисунку 4.9 показано просторову модель для розв’язання цієї типової задачі. Розглянемо приклад, який наведено на рисунку 4.10, де пряма а загального положення перетинає площину b (D АВС) загального положення. Через горизонтальну проекцію прямої а₁ проводять допоміжну площину окремого положення – горизонтально-проекціювальну W ^ П₁. Будують лінію перетину двох площин DE: W Ç b (D АВС) = DE. Отриманий відрізок DE належить площині b (D АВС), тому шукана точка визначається на перетині двох прямих а і DE, що належать площині W:

а Ç DE = К. Видимість прямої а відносно площини b (D АВС) визначається за допомогою двох пар конкуруючих точок. Точки D і F конкурують на П₁: D₁ º(F₁), D Î АВ, F Î а. На П₁ відрізок F₁K₁ проекції прямої а₁ невидимий. Точки G і H конкурують на П₂: H₁ º(G₁), H Î а, G Î АС. На П₂ відрізок F₂K₂ проекції прямої а₂ – видимий.

Рисунок 4.9	Рисунок 4.10

На рисунку 4.11 наведено приклад, де пряма а загального положення перетинає площину S загального положення, яка задана слідами.

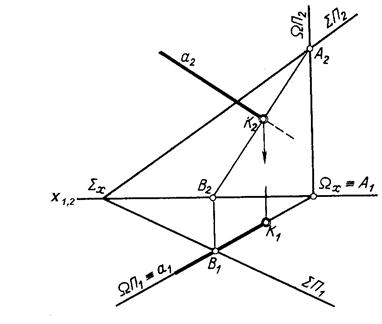
Рисунок 4.11

Дата добавления: 2014-11-08