
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №2. Тема:Элементы математической статистики
|
|
|
|
Тема: Элементы математической статистики.
Цель лекции: Выявление связи эконометрики с теорией вероятностей и математической статистикой
План лекции: Случайные величины.
Функция распределения, плотность распределения и их свойства. Числовые характеристики распределения случайных величин. Параметры распределения. Точечные и интервальные оценки. Проверка статистических гипотез.
Случайной величиной (переменной) называется величина, которая под воздействием случайных факторов может с определёнными вероятностями принимать те или иные значения из некоторого множества чисел.
Случайные величины обозначаются большими буквами ( ), а их возможные значения – малыми (
), а их возможные значения – малыми (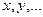 ).
).
Для полной характеристики случайной величины должны быть указаны не только все её значения, но и их вероятности.
Универсальным способом задания случайной величины  является задание её функции распределения.
является задание её функции распределения.
Функцией распределения 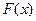 случайной величины
случайной величины  называется вероятность того, что величина
называется вероятность того, что величина  принимает значение, меньшее
принимает значение, меньшее 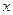 , т.е.
, т.е.  ,
,  .
.
Свойства функции распределения:
1. 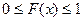 ,
,
2. 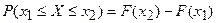 ,
,
3. 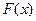 - неубывающая функция, т.е.
- неубывающая функция, т.е. 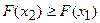 , если
, если 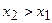 .
.
4. Если возможные значения случайной величины принадлежат интервалу  , то: а)
, то: а) 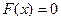 при
при 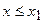 и б)
и б) 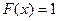 при
при 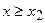 .
.
Случайные величины, в зависимости от того, какой вид имеют множества принимаемых значений, делятся на дискретные и непрерывные.
Случайная величина называется дискретной, если множество всех её возможных значений конечно или счётно.
Дискретную случайную  величину удобнее задавать не в виде функции распределения, а в виде ряда распределения.
величину удобнее задавать не в виде функции распределения, а в виде ряда распределения.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
Закон распределения дискретной случайной величины  удобно задавать таблицей:
удобно задавать таблицей:

| 
| 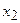
| … | 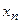
|
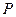
| 
| 
| … | 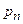
|
где  ,
,  .
.
Случайная величина называется непрерывной, если множество всех её возможных значений бесконечно, т.е. целиком заполняет некоторый числовой промежуток.
Вместо функции распределения 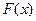 для непрерывной случайной величины обычно используется плотность распределения вероятностей
для непрерывной случайной величины обычно используется плотность распределения вероятностей 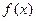 .
.
Плотностью распределения 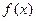 непрерывной случайной величины называется производная от функции распределения, т.е.
непрерывной случайной величины называется производная от функции распределения, т.е. 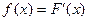 .
.
Из определения производной вытекает вероятностный смысл плотности распределения:
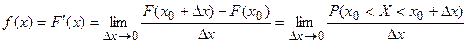
т.е. предел отношения вероятности попадания случайной величины  в интервал
в интервал  к длине этого интервала при
к длине этого интервала при 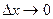 равен значению плотности распределения вероятностей
равен значению плотности распределения вероятностей 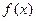 .
.
Из определения плотности распределения следует, что функция распределения 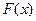 является первообразной для плотности распределения
является первообразной для плотности распределения 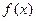 .
.
Свойства плотности распределения:
1. 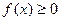 при любых
при любых  ,
,
2. 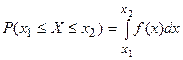 ,
,
3. 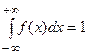 , в частности
, в частности 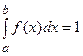 .
.
Зная плотность распределения 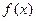 , можно найти функцию распределения
, можно найти функцию распределения 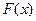 по формуле:
по формуле:
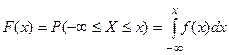 .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 445; Нарушение авторских прав?; Мы поможем в написании вашей работы!