Лекция №4. Тема лекции:Нелинейные регрессии

Тема лекции: Нелинейные регрессии.

Цель лекции: изучение социально-экономических явлений и процессов, которые не выражаются линейными функциями

План лекции: Нелинейность по переменным, нелинейность по параметрам. МНК. Ковариация и корреляция.

Соотношения, существующие между социально-экономическими явлениями и процессами, далеко не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки. В таких случаях используют (по объясняющей переменной) нелинейную регрессию.

Выбор вида уравнения регрессии производится на основании визуального наблюдения расположения точек корреляционного поля.

Нелинейность регрессии проявляется как по переменным, так и по параметрам.

Нелинейность по переменным устраняется путём замены переменной. Например, нелинейные уравнения видов:

после замены - ;

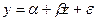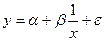после замены - .

Нелинейность по параметру часто устраняется путём логарифмического преобразования уравнения. Например:

степенная функция ~ ;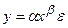

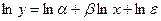экспоненциальная функция ~ .

В экономике функции вида 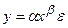применяются при моделировании кривых спроса, а вида - при моделировании временных трендов.

Наиболее часто встречаются уравнения нелинейной регрессии в виде показательной , гиперболической 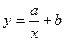или параболической функции.

Для определения неизвестных параметров используют метод наименьших квадратов.

Системы нормальных уравнений имеют вид:

1. для показательной функции

,

2. для гиперболической функции

,

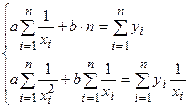3. для параболической функции

.

В экономическом анализе часто используется эластичность функции. Эластичность функции рассчитывается как относительное изменение 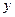к относительному изменению 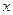, т.е.

Эластичность показывает, на сколько процентов изменяется функция при изменении независимой переменной на 1 %.

В силу того, что эластичность линейной функции не является постоянной величиной, а зависит от 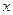, т.е.

,

обычно рассчитывается средний показатель эластичности по формуле

,

где 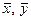- средние значения переменных 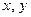в выборке.

Например, для зависимости расходов на питание от доходов средний показатель эластичности равен 0,55 и показывает, что с увеличением дохода на 1 % расходы на питание возрастут в среднем на 0,55 %.

Для степенной функции эластичность представляет собой постоянную величину, равную .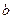

Пусть зависимость расходов на питание от дохода . Эластичность спроса на продукты питания по доходу составляет 0,374. Это означает, что увеличение личного дохода на 1 % при ведёт к увеличению расходов на питание на 0,374 %.

Коэффициент 6,13 не имеет экономического смысла. Он помогает прогнозировать значения 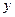при заданных значениях 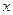, приводя их к единому масштабу.

Дата добавления: 2014-11-18