Оценка существенности параметров линейной регрессии и корреляции. Прогнозирование в регрессионных моделях

.

..

.

Метод наименьших квадратов. Предпосылки регрессионного анализа. Расчет стандартных ошибок коэффициентов регрессии.

Пусть изучается система количественных признаков (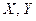). В результате 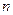независимых опытов получены 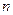пар чисел 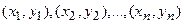. Пусть точки с данными координатами расположены около плавной линии, являющейся графическим изображением функциональной зависимости между ними. Необходимо найти уравнение этой линии.

На рисунке приведены диаграмма рассеяния наблюдений и линии регрессии.

...

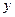
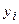
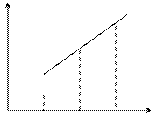
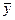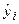
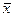
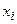
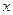
Величина 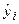описывается как расчетное значение переменной 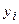, соответствующее 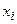. Наблюдаемые значения 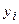не лежат в точности на линии регрессии, т.е. не совпадают с .

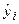Определим остаток 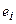в 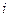-м наблюдении как разность между фактическим и расчетным значениями зависимой переменной, т.е. .

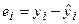Неизвестные значения определяются методом наименьших квадратов ( МНК). Суть МНК заключается в минимизации суммы квадратов остатков:

.

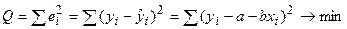Здесь 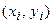- известные значения наблюдения (числа), а - неизвестные.

Использовав необходимое условие экстремума функции нескольких переменных, и после некоторых преобразований, получим систему нормальных уравнений:

.

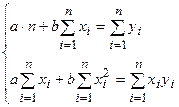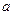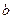Решив систему линейных уравнений относительно параметров и , получим искомую линию регрессии:

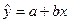или .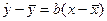

Коэффициент 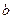есть угловой коэффициент регрессии, он показывает, на сколько единиц в среднем изменяется переменная 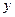при увеличении независимой переменной 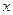на единицу.

Постоянная 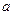даёт прогнозируемое значение зависимой переменной при 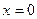. Это может иметь смысл в зависимости от того, как далеко находится 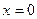от выборочных значений .

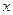После построения уравнения регрессии наблюдаемые значения 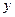можно представить как:

.

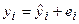Остатки 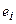, как и ошибки 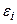, являются случайными величинами, однако, они, в отличие от 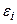, наблюдаемы.

Предпосылки регрессионного анализа. Расчет стандартных ошибок коэффициентов регрессии.

Под прогнозированием в эконометрике понимается построение оценки зависимой переменной для некоторого набора независимых переменных, которых нет в исходных наблюдениях.

Различают точечное и интервальное прогнозирование. В первом случае оценка – некоторое число, во втором – интервал, в котором находится истинное значение зависимой переменной с заданным уровнем значимости.

Рассмотрим регрессионную модель

.

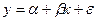Действительное значение зависимой переменной при

,

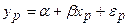где 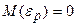, 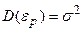. Значения 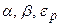неизвестны.

Предсказанным значением является оценка 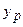(точечный прогноз):

.

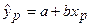Ошибка предсказания равна разности между предсказанным и действительным значениями:

.

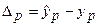Ошибка предсказания имеет нулевое математическое ожидание:

.

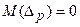Действительно,

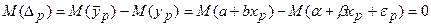
Вычислим дисперсию прогноза. Учитывая, что в случае парной регрессии:

, , ,

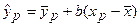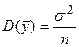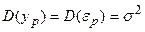для дисперсии прогноза получим:

.

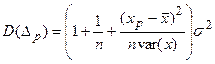Из формулы следует, что чем больше 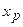отклоняется от выборочного среднего 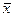, тем больше дисперсия ошибки предсказания, и чем больше дисперсия ошибки предсказания, и чем больше объём выборки 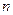, тем меньше дисперсия.

Заменяя в дисперсии прогноз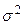а на 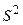и извлекая квадратный корень, получим стандартную ошибку предсказания:

.

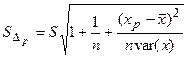Доверительный интервал для действительного значения 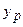определяется выражением:

,

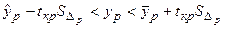где 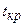- критическое значение -статистики при заданном уровне значимости и числе степеней свободы.

Вопросы для контроля:

1. Поясните значения параметров уравнения парной регрессии.

2. В чем заключается суть МНК?

3. Что понимается под прогнозированием в эконометрике?

Литература

1. МагнусВ. Эконометрика. Москва, 2005г.

2. Доугерти Кр. Введение в эконометрику / Пер. с англ. М. ИНФРА-М, 1997

Дополнительная литература

1. Кулинич Е.И. Эконометрия – М.: Финансы и статистика, 2000.

2. Кремер Н.Ш., Путко Б.А. Эконометрика. М.: ЮНИТИ, 2002.

3. Гмурман В.С. Теория вероятностей и математическая статистика. Москва, 1984г.

4. Гмурман В.С. Руководство к решению задач по теории вероятностей и математической статистике. Москва, 1985г.

Дата добавления: 2014-11-18