Параметры распределения. Точечные и интервальные оценки

Характеристики генеральной совокупности обычно неизвестны. Задача заключается в их оценке по характеристикам выборочной совокупности.

Характеристики генеральной совокупности принято называть параметрами, а выборочной совокупности – оценками.

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, — точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводит к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами — концами интервала. Интервальные оценки позволяют установить, точность и надежность оценок.

Доверительным называют интервал 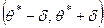, который покрывает неизвестный параметр с заданной надежностью .

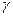Интервал 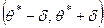имеет случайные концы (их называют доверительными границами). Действительно, в разных выборках получаются различные значения 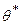. Следовательно, от выборки к выборке будут изменяться и концы доверительного интервала, т.е. доверительные границы сами являются случайными величинами — функциями от .

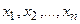Так как случайной величиной является не оцениваемый параметр, а доверительный интервал, то более правильно говорить не о вероятности попадания 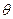в доверительный интервал, а о вероятности того, что доверительный интервал покроет .

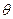Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.

Оценку 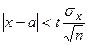называют классической. Из формулы 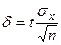, определяющей точность классической оценки, можно сделать следующие выводы:

1) при возрастании объема выборки 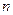число 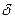убывает и, следовательно, точность оценки увеличивается;

2) увеличение надежности оценки 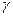приводит к увеличению ( 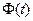— возрастающая функция), следовательно, и к возрастанию 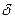; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.

Пусть искомый параметр генеральной совокупности есть 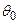, а на основе выборки объёма 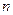определяется оценка .

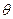Для того, чтобы выборочная оценка давала хорошее приближение оцениваемого параметра, она должна удовлетворять определённым требованиям (несмещенности, эффективности и состоятельности).

Оценка 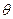называется несмещенной, если её математическое ожидание равно оцениваемому параметру при любом объёме выборки, т.е. .

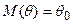Если это не так, то оценка называется смещенной, а разность 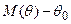- смещением.

Выборочная средняя 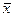является несмещенной оценкой генеральной средней 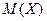, так как 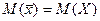. Тем не менее оценка 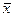не единственная возможная несмещенная оценка .

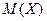Выборочная дисперсия 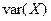является смещенной оценкой генеральной дисперсии 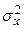, при этом:

.

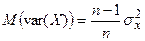В качестве несмещенной оценки генеральной дисперсии используется величина (исправленная дисперсия):

,

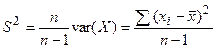для которой .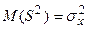

Величина 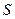называется стандартным отклонением случайной величины в выборке.

Несмещенная оценка 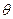называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками, т.е. .

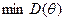Выборочная средняя 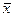является эффективной оценкой генеральной средней, т.е. имеет наименьшую дисперсию в классе несмещенных оценок.

Оценка 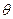называется состоятельной, если при 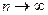она стремится по вероятности к оцениваемому параметру 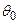, т.е.

.

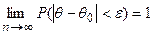Иначе говоря, состоятельной называется такая оценка, которая даёт точное значение для большой выборки независимо от входящих в неё конкретных наблюдений.

Теорема Чебышева закона больших чисел утверждает, что

,

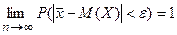т.е. выборочная средняя 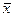является состоятельной оценкой генеральной средней .

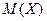Дата добавления: 2014-11-18