
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коварация и корреляция
|
|
|
|
Различают выборочную и теоретическую ковариацию.
Выборочной ковариацией двух переменных 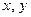 называется средняя величина произведения отклонений этих переменных от своих средних, т.е.
называется средняя величина произведения отклонений этих переменных от своих средних, т.е.
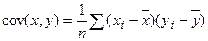 или
или 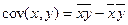 ,
,
где 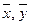 - выборочные средние переменных
- выборочные средние переменных 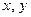 .
.
Заметим, что:
 .
.
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
Теоретической ковариацией случайных величин  называется математическое ожидание произведения отклонений этих величин от своих средних значений, т.е.
называется математическое ожидание произведения отклонений этих величин от своих средних значений, т.е.
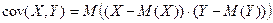 .
.
Свойства теоретической ковариации:
1.  ,
,
2. Если  независимы, то теоретическая ковариация равна нулю
независимы, то теоретическая ковариация равна нулю 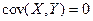 .
.
Говорят, что переменные  положительно (прямо) коррелированны, если
положительно (прямо) коррелированны, если 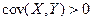 и отрицательно (обратно) коррелированы, если
и отрицательно (обратно) коррелированы, если 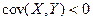 .
.
Более точной мерой зависимости между величинами является коэффициент корреляции. Различают выборочный и теоретический коэффициенты корреляции.
Выборочный коэффициент корреляции определяется выражением:
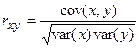 , где
, где 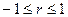 .
.
Если  , то случайные величины
, то случайные величины 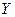 и
и  некоррелированы и могут быть как зависимыми, так и независимыми, если
некоррелированы и могут быть как зависимыми, так и независимыми, если 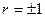 , то
, то 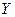 и
и  коррелированны. Отсюда следует, что коэффициент корреляции
коррелированны. Отсюда следует, что коэффициент корреляции 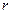 измеряет степень (тесноту) линейной связи между
измеряет степень (тесноту) линейной связи между 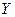 и
и  .
.
Выборочный коэффициент корреляции является случайной величиной.
Теоретический коэффициент корреляции определяется выражением:
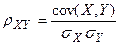 , где
, где 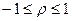 ,
,
где 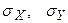 - средние квадратичные отклонения случайных величин
- средние квадратичные отклонения случайных величин  .
.
Теоретический коэффициент корреляции показывает тесноту линейной связи двух случайных величин:
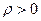 при положительной связи и
при положительной связи и 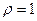 при строгой положительной линейной связи;
при строгой положительной линейной связи;
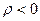 при отрицательной связи и
при отрицательной связи и 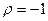 при строгой отрицательной линейной связи;
при строгой отрицательной линейной связи;
 при отсутствии линейной связи.
при отсутствии линейной связи.
Случайные величины 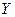 и
и  называются некоррелироваными, если
называются некоррелироваными, если  , и коррелированными, если
, и коррелированными, если 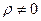 .
.
Свойства:
1. Равенство  указывает на отсутствие линейной связи между переменными, но не на отсутствие связи между ними вообще.
указывает на отсутствие линейной связи между переменными, но не на отсутствие связи между ними вообще.
2. Если  для генеральной совокупности, это не обязательно означает, что
для генеральной совокупности, это не обязательно означает, что  для выборочной совокупности.
для выборочной совокупности.
Проверка гипотезы о корреляции случайных величин.
Пусть по данным выборки объёма 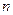 получен выборочный коэффициент корреляции
получен выборочный коэффициент корреляции 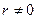 . Требуется проверить гипотезу о равенстве нулю истинного значения коэффициента корреляции, т.е.
. Требуется проверить гипотезу о равенстве нулю истинного значения коэффициента корреляции, т.е.  .
.
В качестве критерия проверки гипотезы 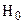 принимается случайная величина
принимается случайная величина 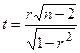 .
.
Величина  при справедливости гипотезы
при справедливости гипотезы 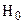 имеет распределение Стьюдента (
имеет распределение Стьюдента ( -статистика) с
-статистика) с 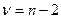 степенями свободы.
степенями свободы.
Сравнивая наблюдаемое значение критерия  с критическим значением
с критическим значением 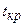 , определяемым по таблице по заданному уровню значимости
, определяемым по таблице по заданному уровню значимости 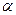 и по числу степеней свободы, получим, что:
и по числу степеней свободы, получим, что:
если 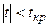 , то
, то 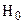 принимается, т.е. нет линейной связи между переменными;
принимается, т.е. нет линейной связи между переменными;
если 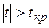 , то
, то 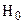 отвергается, т.е. имеется линейная связь между переменными.
отвергается, т.е. имеется линейная связь между переменными.
Вопросы для контроля:
1. В чем отличие нелинейности по переменным от линейности по параметрам?
2. МНК для нахождения параметров нелинейной регрессии.
3. Теоретический коэффициент корреляции, выборочный коэффициент корреляции.
Литература
1. МагнусВ. Эконометрика. Москва, 2005г.
2. Доугерти Кр. Введение в эконометрику / Пер. с англ. М. ИНФРА-М, 1997
Дополнительная литература
1. Кулинич Е.И. Эконометрия – М.: Финансы и статистика, 2000.
2. Кремер Н.Ш., Путко Б.А. Эконометрика. М.: ЮНИТИ, 2002.
3. Гмурман В.С. Теория вероятностей и математическая статистика. Москва, 1984г.
4. Гмурман В.С. Руководство к решению задач по теории вероятностей и математической статистике. Москва, 1985г.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 2741; Нарушение авторских прав?; Мы поможем в написании вашей работы!