Лекция №1. Тема лекции:Модель множественной регрессии

Модуль №2

Тема лекции: Модель множественной регрессии. Анализ вариации зависимой переменной.

Цель лекции: составление уравнения множественной регрессии, исследование параметров уравнения множественной регрессии.

План лекции: классическая модель линейной множественной регрессии. Множественный и частный коэффициент корреляции.

Обобщением линейной регрессионной модели с одной объясняющей переменной является линейная регрессионная модель с 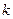объясняющими переменными (модель множественной регрессии):

,

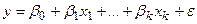где - параметры модели, а 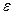- случайный член.

Случайный член 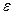удовлетворяет тем же предпосылкам, что и в модели с парной регрессией. Предполагается, что объясняющие переменные некоррелированы друг с другом.

На основе 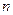наблюдений оценивается выборочное уравнение регрессии:

,

где 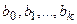- оценки параметров .

Для оценки параметров регрессии используется метод наименьших квадратов. В соответствии с МНК минимизируется сумма квадратов остатков:

.

Необходимым условием её минимума является равенство нулю всех её частных производных по .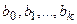

В результате приходим к системе из 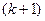линейного уравнения с 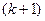неизвестным, называемой системой нормальных уравнений. Её решение в явном виде обычно записывается в матричной форме, иначе оно становится слишком громоздким.

Оценки параметров модели и их теоретические дисперсии в матричной форме определяются выражениями:

, ,

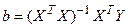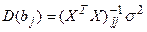где 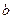- вектор с компонентами 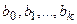; - матрица значений объясняющих переменных; 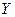- вектор значений зависимой переменной; 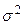- дисперсия случайного члена.

Несмещенной оценкой 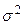является величина 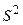(остаточная дисперсия):

.

Величина 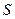называется стандартной ошибкой регрессии.

Заменяя в теоретических дисперсиях неизвестную дисперсию 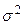на её оценку 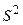и извлекая квадратный корень, получим стандартные ошибки оценок коэффициентов регрессии:

.

Если предпосылки относительно случайного члена 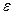выполняются, оценки параметров множественной регрессии являются несмещенными, состоятельными и эффективными.

При использовании компьютерных программ коэффициенты регрессии 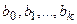и их стандартные отклонения вычисляются одновременно.

Пусть в уравнении регрессии содержатся 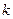объясняющих переменных. Допустим, что можно разложить дисперсию зависимой переменной на объясненную и необъясненную составляющие:

.

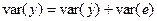Используя определение выборочной дисперсии, это уравнение можно представить в виде:

.

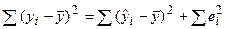Обозначим:

- общий разброс зависимой переменной;

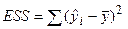- разброс, объясненный регрессией;

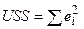- - разброс, не объясненный регрессией.

Тогда

.

(В скобках указано число степеней свободы, соответствующее каждому члену уравнения).

Коэффициент детерминации есть доля объясненной части разброса зависимой переменной, т.е.

.

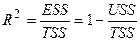Величина является мерой объясняющего качества уравнения регрессии по сравнению с горизонтально линией .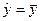

Дата добавления: 2014-11-18