Анализ линейных непрерывных САР: устойчивость САР

ЛЕКЦИЯ №6

Общее понятие устойчивости динамической системы. Особенности устойчивости линейных САР

Дадим более строгое понятие устойчивости динамической системы, которое будет справедливым для всех типов систем, в том числе и нелинейных. Используем для этого следующее геометрическое представление:

Предположим, что для рассматриваемой системы переходные процессы дифференцируемы в каждой точке пространства. Система устойчива, если для любого ρ < R существует такое r ≤ ρ <R, что траектория у(t), начинающаяся в точке у(0), принадлежащей области Sr, остается в сферической области Sρ при t Î [0, ¥]. Система асимптотически устойчива, если она устойчива и, кроме того, каждая траектория системы у(t) начинающаяся в произвольной точке области Sρ при t ® ¥ стремится к началу координат области Sr (к нулю).

R

ρ

r

у(0)

у₁(t)

у₂(t)

у₃(t)

Процессы

Рис. 6.1

Система неустойчива, если для некоторого, хотя бы одного, ρ < R и любого r (каким бы малым оно не было выбрано) всегда найдется внутри области Sr такая точка у(0), что траектория у(t), начинающаяся в этой точке, за конечное время выйдет за пределы сферы Sρ.

Эта формулировка охватывает как линейные, так и нелинейные системы, в частности системы, работающие в режиме автоколебаний. Она предполагает анализ устойчивости на базе методов Ляпунова.

В классе линейных систем анализ устойчивости резко упрощается. Устойчивость линейных систем не зависит от начальных условий, величины и характера входных воздействий. В этом случае анализ устойчивости можно вести только по виду собственного оператора САР, т.е. достаточно анализировать только собственное движение системы. Аналитически - достаточно рассматривать при анализе устойчивости однородные ДУ САР.

Определение устойчивости САР прямыми методами. Виды неустойчивости

Пусть Q^c(p) – собственный оператор САР, тогда однородное ДУ системы имеет вид: Q^c(p)y = 0.

Его решение в общем случае представляет собой сумму:

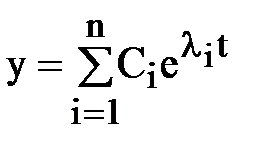, (6.1)

где С_i – постоянная интегрирования (определяется из начальных условий), ;

n – порядок ДУ;

l_i – корни характеристического уравнения Q^c(λ) = 0.

В общем случае в (6.1) l_i являются комплексно-сопряженными:

.

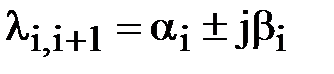В частных случаях при β_i = 0 или α_i = 0 они вырождаются в действительные или чисто мнимые.

Каждая пара сопряженных корней в (6.1) дает свою i-тую составляющую в переходном процессе:

y_i = = ,

где и j_i – постоянные, определяемые из начальных условий.

Из (6.1) следует, что для того чтобы y сходился, т.е. стремился в окрестность нуля, необходимо чтобы все y_i стремились бы в окрестность нуля (сходились). Если хотя б одна составляющая будет расходиться (не будет стремиться в окрестность нуля), то и y в целом будет иметь расходящийся характер.

Проанализируем характер составляющих y_i в y в зависимости от конкретного вида корней, см. рис. 6.2.

Расходящиеся компоненты соответствуют корням с положительной действительной частью (a_i > 0). В том случае, если a_i = 0 (корни чисто мнимые), то система находится на границе устойчивости – переходные процессы в ней и не сходятся и не расходятся.

Движение системы на границе устойчивости является неустойчивым видом движения, т.к. любые сколько угодно малые изменения параметров системы (объекта или регулятора) приведут к расходящимся или сходящимся процессам.

Фактически движение САР на границе устойчивости – математическая абстракция. Практическая вероятность того, что и у объекта, и у регулятора могут оказаться такие параметры, что система окажется строго на границе устойчивости равна нулю.

Корни знаменателя передаточной функции системы Q^c(λ) называются полюсами передаточной функции.

Если воспользоваться приемом отображения корней полинома на комплексной плоскости точками (см. рис. 6.3), то сформулированный ранее вывод об устойчивости системы можно перефразировать так: «расположение полюсов передаточной функции САР для ее устойчивости должно быть «левым» (т.е. все действительные корни и действительные части комплексно-сопряженных корней должны быть отрицательными)».

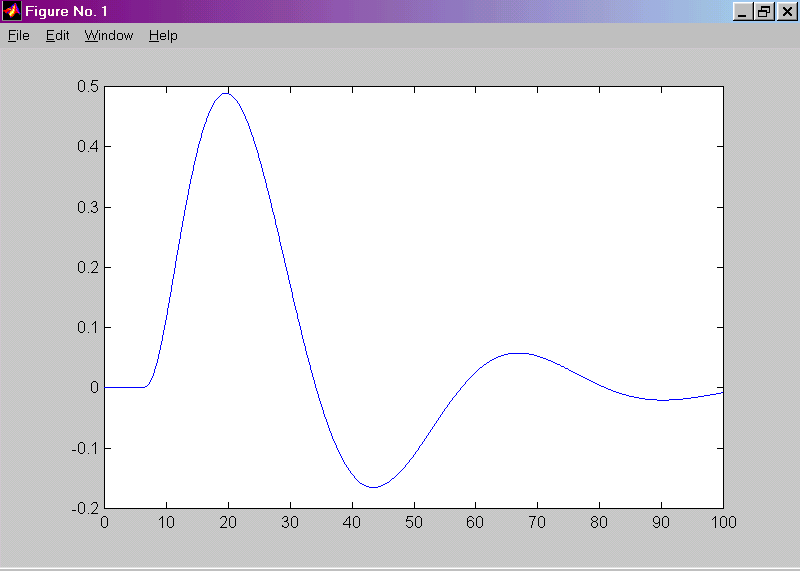
1. Корни действительные (β_i = 0) 2. Корни комплексные (β_i ¹ 0,a_i < 0)

t

y_i(0)

y_i

t

y_i(0)

y_i

α_i > 0

α_i = 0

α_i < 0

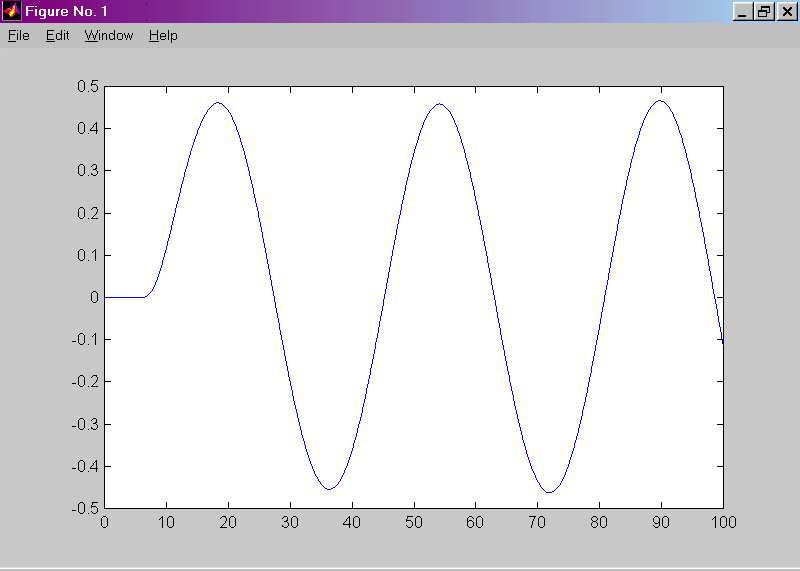
3. Корни комплексные (β_i ¹ 0,a_i > 0) 4. Корни чисто мнимые (β_i ¹ 0,a_i = 0)

t

y_i(0)

y_i

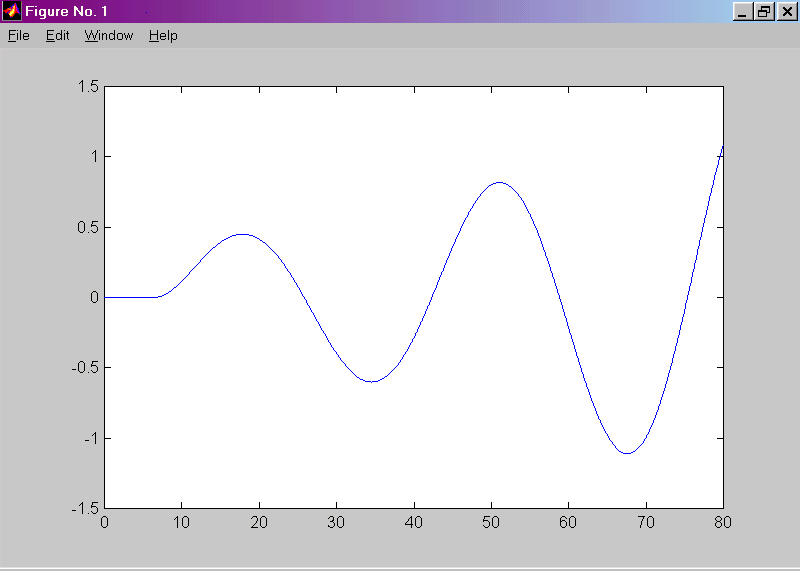
t

y_i(0)

y_i

Рис. 6.2

Примеры расположения корней САР 4-го порядка и ее устойчивость:

Дата добавления: 2014-11-08