Задачи структурного и параметрического синтеза

Декомпозиция задачи синтеза.

Типичные ограничения

Типичные критерии оптимальности

В практике управления технологическими процессами наиболее часто используют в качестве критериев оптимальности следующие показатели качества:

а) показатели качества переходных процессов, прежде всего интегральные;

б) показатели качества установившихся процессов в САР (среднеквадратическое отклонение и математическое ожидание ошибок);

в) показатели быстродействия (времени переходного процесса);

г) компромиссные показатели качества, которые представляют собой композицию различных показателей, входящих в общий со своими весовыми коэффициентами.

1) Ограничения на структуру УУ:

а) ограничения, связанные с принципиальными возможностями физической реализации некоторых алгоритмов. Например, принципиально невозможно реализовать звенья чистого опережения и дробно-рациональные функции, порядок числителя которых выше порядка знаменателя;

б) ограничения, связанные с ограничением сложности алгоритма, в частности с ограничением порядка используемых в алгоритме производных. Производные высоких порядков существенно снижают помехозащищенность алгоритма, т.к. являются усилителями высоких частот;

в) ограничения, связанные с номенклатурой используемых технических средств, для реализации УУ.

2) Ограничения на параметры УУ

а) ограничения, связанные с физическими ограничениями на коэффициенты передачи (усиления и скорости изменения переменных);

б) ограничения, связанные с фактическими диапазонами изменения коэффициентов в конкретных технических средствах.

Формально задача (11.1) т.е. задача отыскания j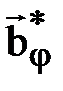^*, может решаться как задача «аналитического конструирования регулятора». Однако, с математической точки зрения эта задача очень сложна, и главное:

а) конечный результат синтеза в явном виде может быть получен только при большом количестве упрощений и допущений. Они могут выхолостить суть задачи и найденное решение не даст на практике ожидаемого результата;

б) часто найденные алгоритмы оказываются негрубыми;

в) найденные алгоритмы часто оказываются физически нереализуемыми (если ОУ имеет запаздывание, то в УУ появляется чистое опережение);

г) используемый критерий («критерий обобщенной работы» - квадратичный критерий, который помимо ошибки регулирования Dy штрафует дополнительно производную от управляющего воздействия), по сути дела, подбирается под решение задачи аналитического конструирования, а не отражает действительные потребности практики.

Использование метода аналитического конструирования регуляторов возможно только для хорошо определенных объектов. Для технологических ОУ его применение не дает хороших результатов.

В связи с этим в инженерной практике при разработке систем управления для промышленных ОУ задачу синтеза подвергают декомпозиции, т.е. ее подразделяют на две взаимосвязанные задачи:

– задача 1 – структурный синтез УУ – определяется 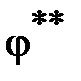Î ,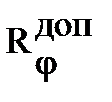

где 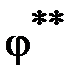– квазиоптимальный алгоритм, который получают с помощью процедуры неоптимального синтеза; эта процедура учитывает особенности ОУ, предъявляемые к САР требования и основывается на апробированных практикой подходах;

– задача 2 – параметрический синтез (параметрическая оптимизация алгоритма ): = arg min(max) .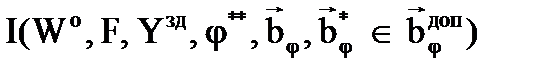

Дата добавления: 2014-11-08