Критерии, используемые в инженерных методиках синтеза

Параметрический синтез типовых САР

Выбор типовых алгоритмов для САР означает, что на этапе структурного синтеза разработчик остановил свой выбор на типовых алгоритмах управления. Отметим, что типовые алгоритмы не противоречат решению общей задачи оптимального синтеза, т.к. являются линейными.

Для инженерной практики типовые алгоритмы удобны тем, что имеется широкая номенклатура программных и технических средств для их реализации, хорошая методическая поддержка разработчика (методики параметрической идентификации типовых моделей объектов и методики расчета настроечных параметров регуляторов).

Под инженерными методиками синтеза САР понимают методики расчета настроечных параметров регуляторов по известным свойствам ОР и при сформулированных требованиях к качеству переходных процессов (переходных характеристик). Синтез САР по инженерным методикам не решает задачу параметрической оптимизации САР. Вместе с тем, сущность процесса разработки методик этого синтеза такова, что задачи параметрической оптимизации САР лежат в основе методик. Эти методики несут в себе компромисс между простотой применения и качеством настройки регулятора. В тех случаях, когда процедура оптимального параметрического синтеза предусмотрена и выполняется, то расчет параметров регулятора по инженерным методикам можно рассматривать как первый этап этой процедуры – расчет начальных приближений оптимизируемых параметров.

Поскольку в инженерных методиках синтеза процедура оптимизации не предусматривается, то обычно критерий оптимальности не используется. Критерием отбора настроечных параметров является желаемый вид переходного процесса (переходной характеристики). Вместе с тем, анализ этих типов переходных процессов позволяет приближенно указать вид критериев, которые достигали бы своего min при выбранных параметрах регуляторов, если бы процедура оптимизации проводилась.

В принципе, существует большое количество инженерных методик. Рассмотрим две наиболее простые и широко распространенные. В этих методиках задают три вида переходных процессов, которые желательны:

1) апериодический переходный процесс (далее – ПП). Такой ПП соответствует критериям: 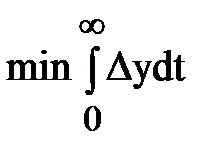; min t_рег, y = 1…0,95.

2) колебательный ПП с R_п = 20 %, 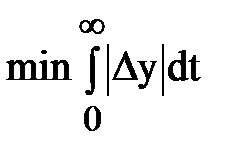, y = 0,95…0,85.

3) колебательный ПП с R_п = 40 %, 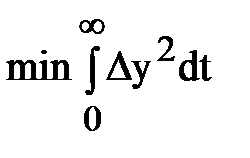, y = 0,85…0,75.

Другие особенности методик:

а) рассматриваются модели объекта (канала регулирования) первого порядка с запаздыванием;

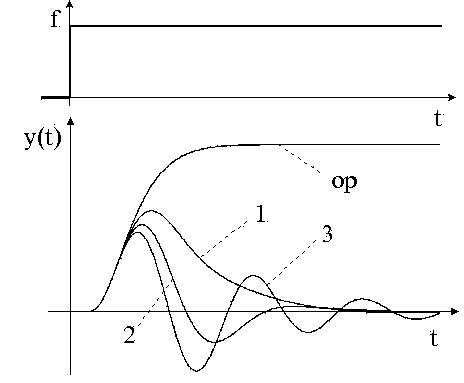
б) возмущения считаются приведенными к каналу регулирования; в) возмущения являются ступенчатыми.

Рис. 11.1

Методика расчета настроечных параметров регуляторов Копеловича А.П. (с использованием формул)

а) статический ОР

Тип регулятора	Тип ПП
Апериодический	Колебат. с Rп = 20 %	Колебат. с Rп = 40 %
П-	kp= 0,3To/(ko·to)	kp = 0,7To/(ko·to)	kp = 0,9To/(ko·to)
ПИ-	kp= 0,6To/(ko·to) Тиз =3,2·to	kp = 0,8To/(ko·to) Тиз =2,5·to	kp = 1,1To/(ko·to) Тиз =2·to
ПИД-	kp= 0,8To/(ko·to) Тиз =2,4·to Тпр =(0,5…1) to	kp = 1,0To/(ko·to) Тиз =2,0·to Тпр =(0,5…1) to	kp = 1,2To/(ko·to) Тиз =1,4·to Тпр =(0,5…1) to

б) астатический ОР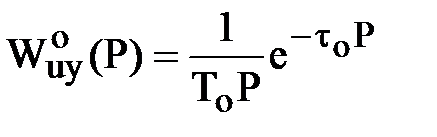

Тип регулятора	Тип ПП
Апериодический	Колебат. с Rп = 20 %	Колебат. с Rп = 40 %
П-	kp = 0,4To/to	kp = 0,7To/to	kp = 1,0To/to
ПИ-	kp = 0,4To/to Тиз =6·to	kp = 0,7To/to Тиз =4·to	kp = 0,7To/to Тиз =3·to
ПИД-	kp = 0,6To/to Тиз =5·to Тпр =(0,5…1) to	kp = 1,1To/to Тиз =2·to Тпр =(0,5…1) to	kp = 1,4To/to Тиз =1,5·to Тпр =(0,5…1) to

Методика расчета настроечных параметров регулятора Копеловича А.П. – Клюева А.С. (с использованием номограмм)

Дает возможность определить настроечные параметры регулятора по номограммам. В качестве желаемого характера ПП используется показатель y, который ввел Клюев. У Копеловича был коэффициент перерегулирования. Номограммы разработаны для различных типов объектов, различных регуляторов. В номо-

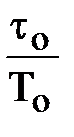
А

А_k

А_Т

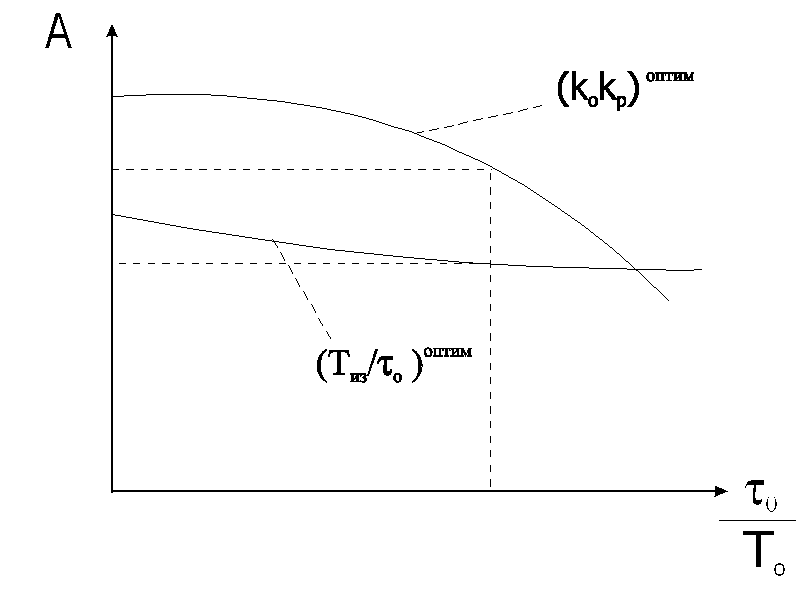
Рис. 11.2

граммах используются безразмерные параметры: k_оk_р; t_o/Т_о; Т_из/t_o, t_пр/t_o.

; .

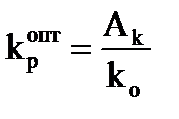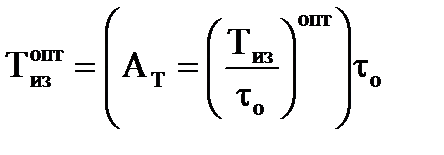Номограммы, взятые из книги «Наладка средств автоматизации и автоматических систем регулирования: Справочное пособие / А.С. Клюев, А.Т. Лебедев, С.А. Клюев, А.Г. Товарнов; Под ред. А.С. Клюева. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1989. – 368 с.: ил.» приведены на рис. 11.3 – 11.8. При этом сохранены обозначения параметров принятых в оригинале. Они интуитивно понятны и не требуют дополнительной расшифровки.

а) б)

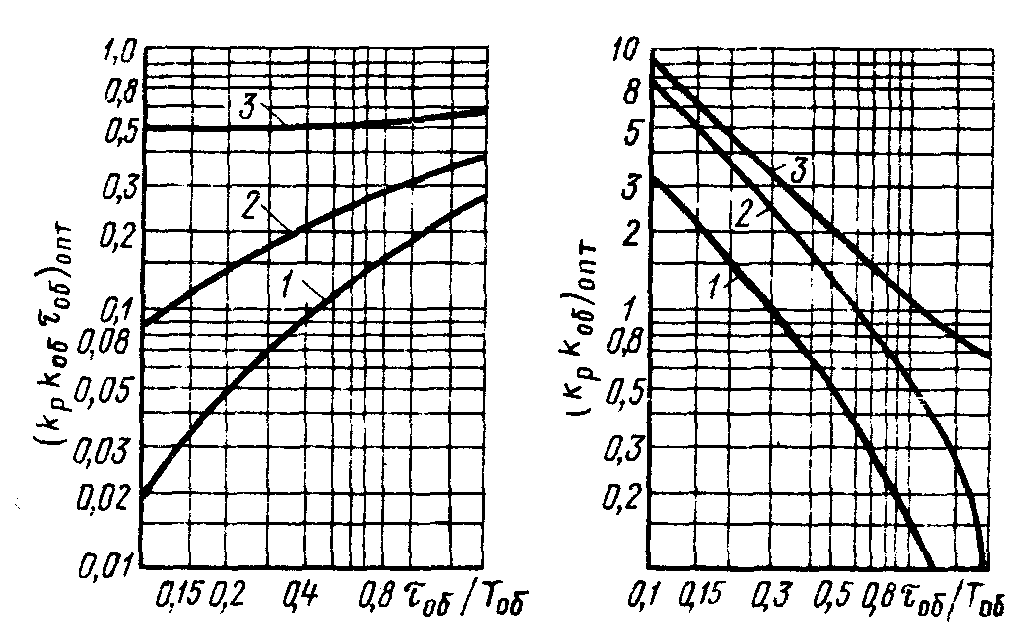
Рис. 11.3. Номограммы для определения оптимальных параметров настройки

И-регулятора (а) и П-регулятора (б) статических объектов:

1 - y = 1,0 ¸ 0,95; 2 - y = 0,95 ¸ 0,85; 3 - y = 0,85 ¸ 0,75

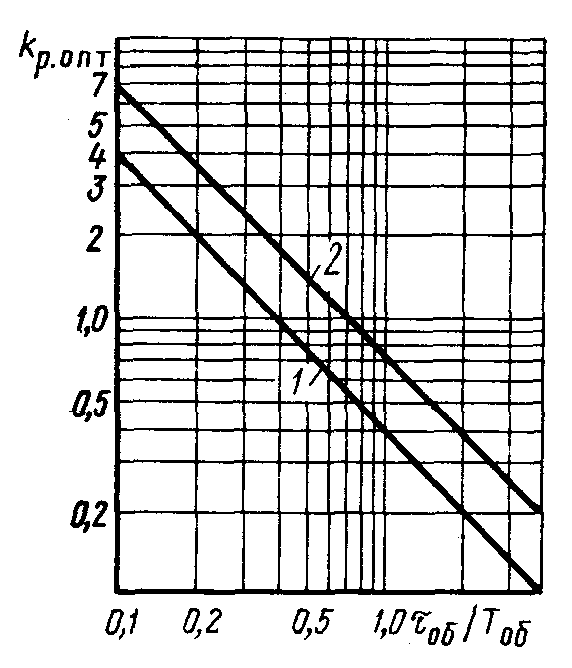
Рис. 11.4. Номограммы для определения оптимальных параметров

настройки П-регулятора астатических объектов:

1 - y = 1,0 ¸ 0,95; 2 - y = 0,95 ¸ 0,85

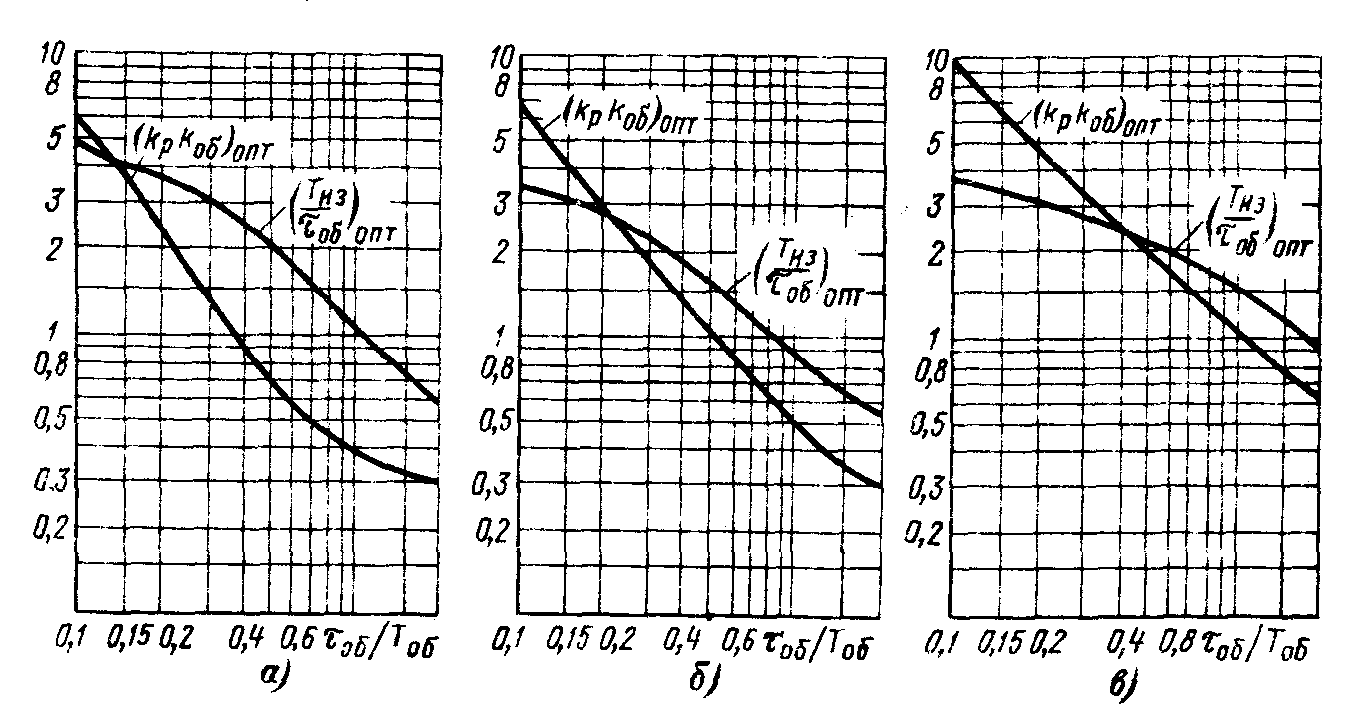
Рис. 11.5. Номограммы для определения оптимальных параметров

настройки ПИ-регулятора статических объектов:

а) - y = 1,0 ¸ 0,95; б) - y = 0,95 ¸ 0,85; в) - y = 0,85 ¸ 0,75

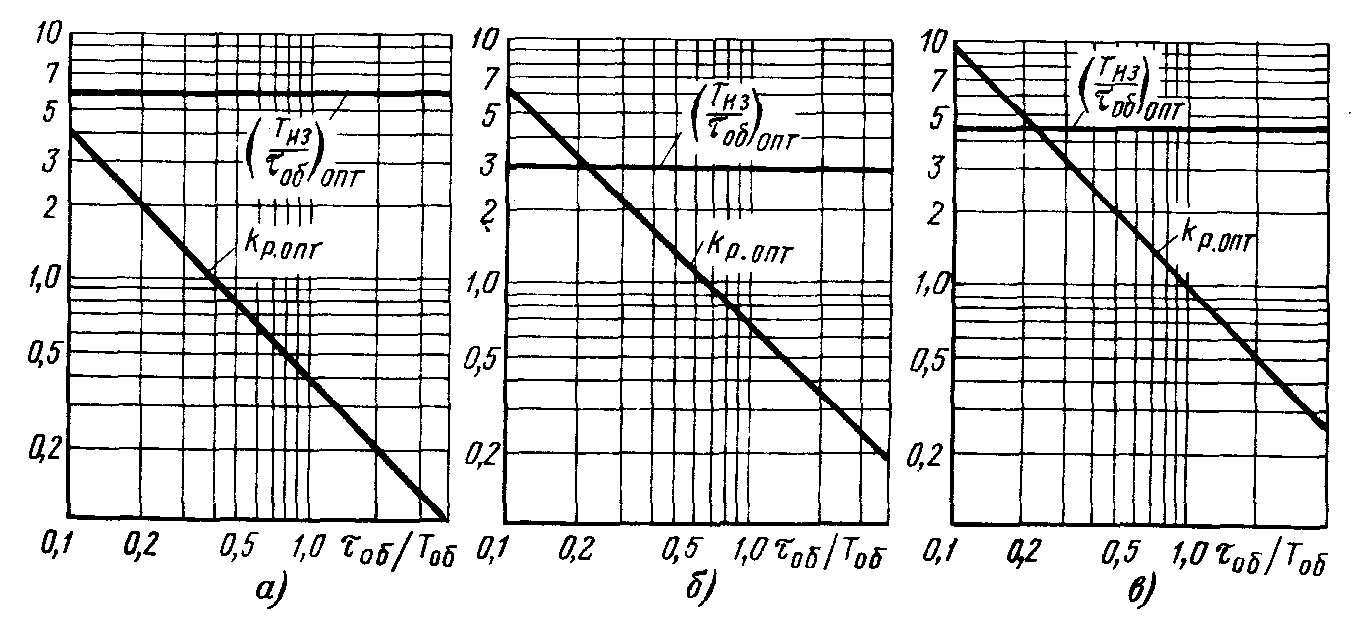
Рис. 11.6. Номограммы для определения оптимальных параметров

настройки ПИ-регулятора астатических объектов:

а) - y = 1,0 ¸ 0,95; б) - y = 0,95 ¸ 0,85; в) - y = 0,85 ¸ 0,75

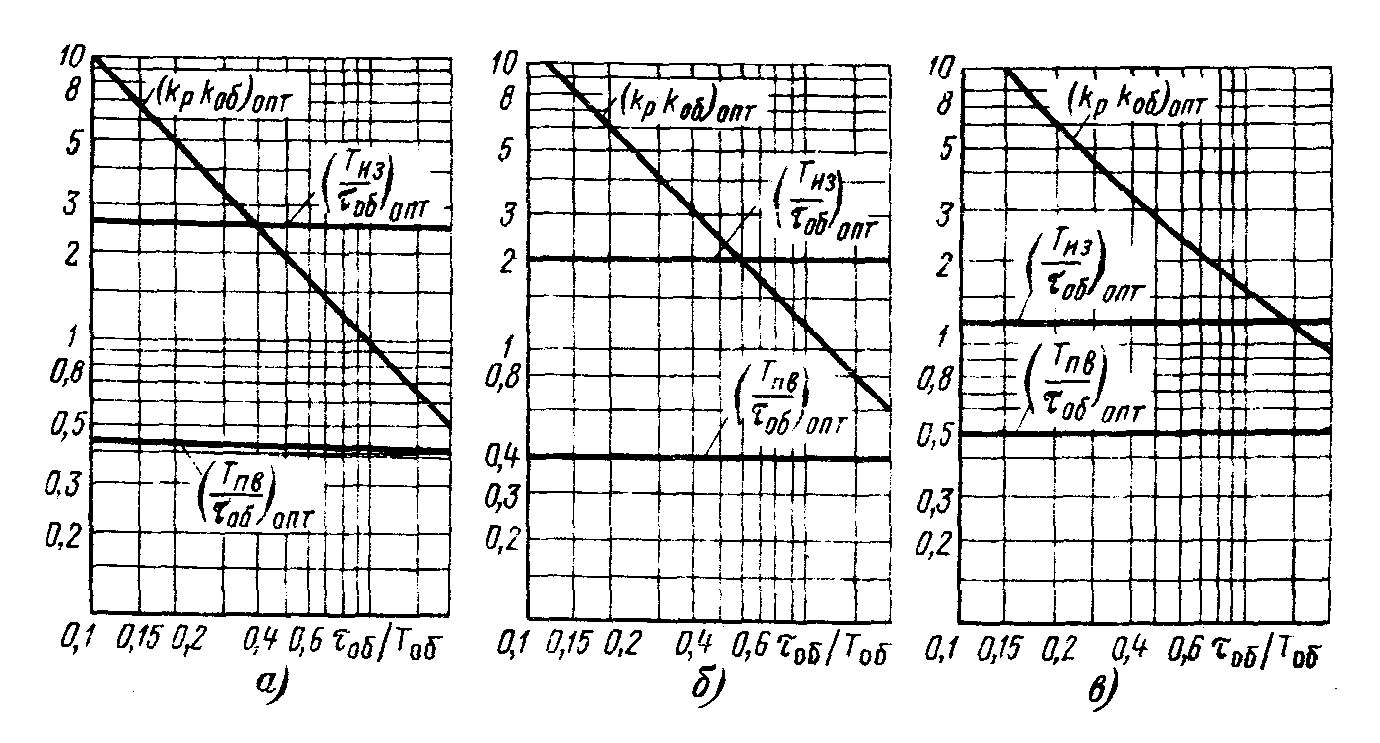
Рис. 11.7. Номограммы для определения оптимальных параметров настройки

ПИД-регулятора статических объектов:

а) - y = 1,0 ¸ 0,95; б) - y = 0,95 ¸ 0,85; в) - y = 0,85 ¸ 0,75

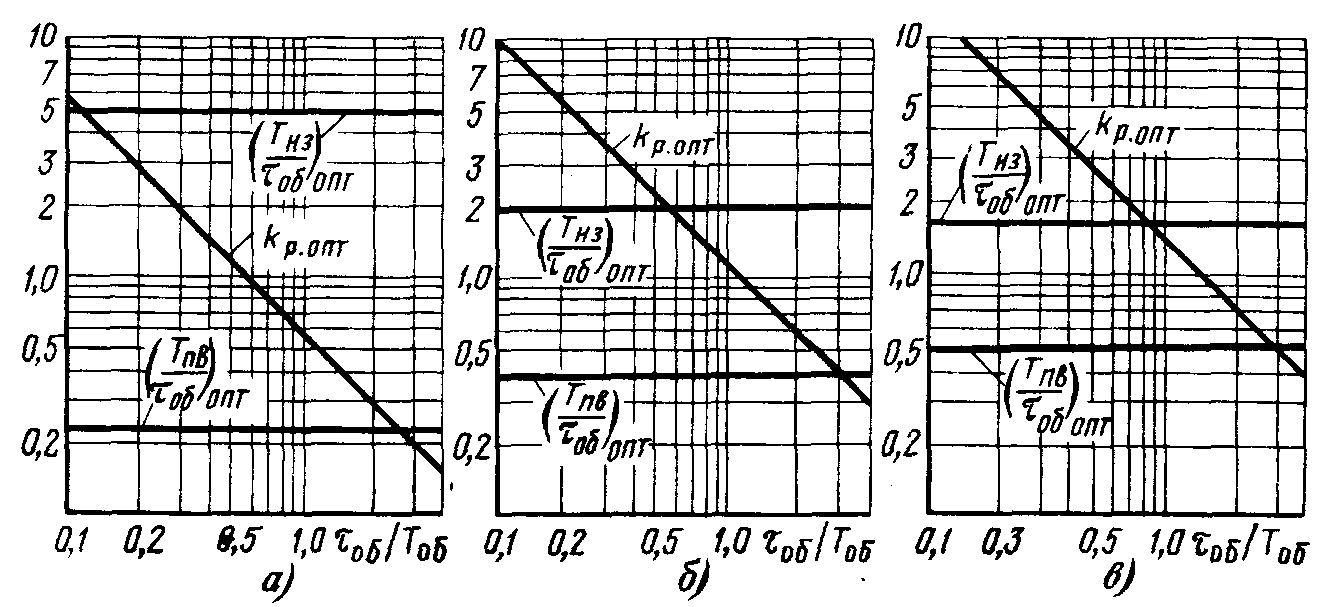
Рис. 11.8. Номограммы для определения оптимальных параметров

настройки ПИД-регулятора астатических объектов:

а) - y = 1,0 ¸ 0,95; б) - y = 0,95 ¸ 0,85; в) - y = 0,85 ¸ 0,75

Дата добавления: 2014-11-08