Решение типовых задач

Задача 1. На 5 карточках разрезной азбуки написаны буквы п, р, с, о, т. Перемешанные карточки вынимаются наудачу по одной и располагаются в одну линию. Какова вероятность прочесть слово "спорт"?

Решение. Искомую вероятность события А (можно прочесть слово "спорт") определим по формуле 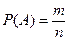. Здесь общее число всевозможных исходов 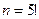– число перестановок из 5 элементов. Благоприятствующим исходам отвечает одно слово "спорт", т. е. . Таким образом, .

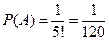Задача 2. Из 9 карточек, занумерованных разными цифрами, выбираются наудачу 3. Найти вероятность того, что последовательная запись их номеров показывает возрастание.

Решение. Трехзначные числа – упорядоченные тройки элементов из 9 цифр – есть размещения из 9 по 3, т.е. 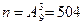. Число благоприятных исходов 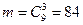. Следовательно, искомая вероятность .

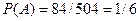Задача 3. Среди 17 студентов группы, в которой 9 юношей, производится розыгрыш 7 билетов лотереи, причем каждый студент может выбрать только один билет. Какова вероятность того, что среди обладателей билетов будет 4 девушки?

Решение. Обозначим событие А – среди 7 обладателей билетов будет 4 девушки. Количество равновозможных способов выбора по 7 человек из 17 равно .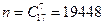

Число благоприятных исходов, т. е. число выборок по 7, в которых 4 девушки сочетаются с 3 юношами, определяется по правилу произведения 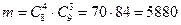. Тогда искомая вероятность .

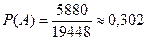Задача 4. В секцию магазина поступило 10 велосипедов, из которых 4 – с дефектами. Наудачу взяты 3. Найти вероятность того, что среди взятых будут: а) все без дефектов; б) все одинакового качества.

Решение. а) Событие А – все 3 наудачу взятые из 10 велосипедов без дефектов. Число возможных исходов 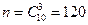. Три велосипеда без дефектов можно выбрать из 6 имеющихся 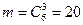способами. Искомая вероятность .

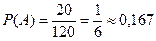б) Событие В – все 3 велосипеда одного качества, т.е. или 3 годные, или 3 с дефектами. Три годные из 6 можно выбрать 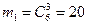способами, а 3 с дефектами из 4 имеющихся 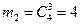способами. Общее число способов выбора 3-х велосипедов одинакового качества по правилу суммы равно 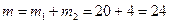. Следовательно, .

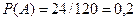Задача 5. Тонкую иглу (точку) бросают на отрезок 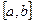. Какая вероятность того, что она попадет на отрезок ?

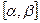Решение. По условию игламожет упасть в любую точку указанного отрезка. В данном случае перечислитьвсе точки отрезка невозможно. Воспользуемся геометрическим определением и в качестве меры выберем длину отрезка 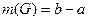. Интересующему нас событию благоприятствует ситуация, когда игла упадет в любую точку отрезка 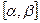. Тогда .

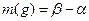Задачи для отчета преподавателю

Блок А

А 1.1. На 6 карточках написаны буквы к, а, р, е, т, а. После того, как их тщательно перемешают, берут наудачу по 1 карточке и кладут последовательно рядом. Какова вероятность того, что получится слово "ракета"?

А 1.2. Из разрезной азбуки выкладывается слово "статистика". Затем все буквы этого слова перемешиваются и снова выкладываются в случайном порядке. Какова вероятность того, что снова получится слово "статистика"?

А 1.3. Из разрезной азбуки составлено слово "треугольник". Ребенок, не умеющий читать, рассыпал эти буквы, а затем выбрал 4 из них и собрал в произвольном порядке. Найти вероятность того, что у него появятся слова: а) "руль"; б) "угол".

А 1.4. Телефонный номер состоит из 7 цифр. Какова вероятность того, что в нем: а) все цифры различны; б) все цифры нечетные; в) все цифры различны и четные?

А 1.5. По линии связи в случайном порядке передаются 30 знаков алфавита. Найти вероятность того, что на ленте появится последовательность букв, образующих слово "режим".

А 1.6. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что они различны, набрал эти цифры наудачу. Какова вероятность того, что набран нужный номер?

А 1.7. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со 2-го. Найти вероятность следующих событий: а) все пассажиры выйдут на 4-м этаже; б) все пассажиры выйдут одновременно (на одном и том же этаже); в) все пассажиры выйдут на разных этажах.

А 1.8. В коробке содержится 4 одинаковых занумерованных кубика. Наудачу по одному извлекают все кубики из коробки. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

А 1.9. Наудачу выбирается пятизначное число. Какова вероятность следующих событий: а) число одинаково читается как слева направо, так и справа налево (например, 12321); б) число кратно 5; в) число состоит из нечетных цифр.

А 1.10. На понедельник в институте запланировано 3 лекции по различным предметам из 10 изучаемых на данном курсе. Какова вероятность того, что студент, не успевший ознакомиться с расписанием, его угадает, если любое расписание из 3 предметов равновозможно?

А 1.11. Из полного набора домино (28 штук) наудачу выбирают 7 костей. Какова вероятность, что среди них окажется: а) по крайней мере одна кость с 5 очками; б) по крайней мере одна кость с 5 или 6 очками?

А 1.12. Из 10 первых букв русского алфавита наудачу составляется новый алфавит, состоящий из 5 букв. Определить вероятность следующих событий: а) в состав нового алфавита входит буква "а"; б) в состав нового алфавита входят только согласные буквы.

А 1.13. Среди кандидатов в студсовет факультета 3 первокурс­ника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек на конференцию. Найти вероятность следующих событий: а) будут выбраны одни третьекурсники; б) все первокурсники попадут на конференцию; в) не будет выбрано ни одного второкурсника.

А 1.14. Из колоды в 52 карты извлекаются наудачу 4 карты. Найти вероятность следующих событий: а) выбраны все карты трефовой масти; б) выбран хотя бы один король.

А 1.15. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равно­возможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода – 1 час, а второго – 3 часа.

А 1.16. На отдельных карточках написаны 12 вариантов контрольной работы, которые распределяются случайным образом среди 10 студентов, сидящих в одном ряду. Найти вероятность следующих событий: а) варианты с номерами 4 и 5 останутся неиспользованными; б) варианты 5 и 10 достанутся рядом сидящим студентам; в) будут распределены последовательные номера вариантов.

А 1.17. Среди 10 студентов, случайным образом занимающих очередь за учебниками в библиотеку, находятся 2 подруги. Какова вероятность того, что в образовавшейся очереди между подругами окажется 4 человека?

А 1.18. Из общего количества костей домино наудачу извлекли 1 кость. Оказалось, что это не дубль. Какова вероятность того, что 2-ю извлеченную кость домино можно будет приставить к 1-й?

А 1.19. В подъезде дома установлен замок с кодом. Дверь автоматически отпирается, если последовательно набрать 2 цифры из имеющихся 10. Некто вошел в подъезд и, не зная кода, стал пробовать различные комбинации, затрачивая на каждую попытку 10 секунд. Какова вероятность того, что вошедшему удастся открыть дверь: а) за 10 минут; б) за 15 минут; в) за 1 час?

А 1.20. В телефонной книге случайно выбирается номер телефона, состоящий из 7 цифр. Найти вероятность того, что: а) четыре последние цифры телефонного номера одинаковы; б) все четыре последние цифры различны.

А 1.21. В ящике имеется 15 деталей, 9 из которых окрашены. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окрашены.

А 1.22. Группа из 8 юношей и 8 девушек делится случайно на 2 равные части. Найти вероятность того, что в каждой части юношей и девушек поровну.

А 1.23. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков будет равна 8, а разность – 4.

А 1.24. На 5 карточках написаны цифры 1, 2, 3, 4, 5. Две из них одна за другой извлекаются. Найти вероятность того, что число на 2-й карточке будет больше, чем на 1-й.

А 1.25. Программа экзамена содержит 20 различных вопросов, из которых студент знает только 10. Для успешной сдачи экзамена достаточно ответить на 2 из 3 предложенных вопросов. Какова вероятность успешной сдачи экзамена?

А 1.26. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее чем на 3 из 4 вопросов билета. Взглянув на 1-й вопрос билета, студент обнаружил, что он его знает. Какова вероятность того, что студент: а) сдаст зачет; б) не сдаст зачет?

А 1.27. В лотерее 100 билетов. Из них 25 выигрышных. Определить вероятность того, что 2 приобретенных билета окажутся выигрышными.

А 1.28. Регистр калькулятора содержит 8 разрядов. Считая, что появление любого числа на регистре случайно, определить вероятность следующих событий: а) во всех разрядах стоят нули; б) во всех разрядах стоят одни и те же цифры; в) регистр содержит только 2 одинаковые цифры; г) регистр содержит только 2 пары одинаковых цифр; д) регистр содержит 3 одинаковые цифры.

А 1.29. Из 7 яблок, 3 апельсинов и 5 лимонов случайным образом в пакет отбирают 5 фруктов. Найти вероятности следующих событий: а) в пакете только 1 апельсин; б) пакет не содержит апельсинов; в) пакет не содержит лимонов; г) пакет не содержит яблок.

А 1.30. Путем жеребьевки разыгрываются 6 подписных изданий среди 12 участников, каждый из которых не может получить более 1 подписки. Найти вероятность того, что из списка получат подписку: а) первые 6 человек; б) первые 3 человека; в) 1-й человек; г) 1-й и 3-й человек.

А 1.31. Подбрасывают наудачу 3 игральные кости. Вычислить вероятности следующих событий: а) на 3 костях выпадут разные грани; б) хотя бы на одной из костей выпадет шестерка.

А 1.32. В ящике лежат 12 красных, 8 зеленых и 10 синих карандашей. Наудачу вынимаются без возвращения 2 карандаша. Найти вероятность того, что окажется не вынутым: а) синий карандаш; б) зеленый карандаш; в) красный карандаш.

А 1.33. Студент знает 14 вопросов из 20. В билете 3 вопроса. Найти вероятность того, что студент ответит хотя бы на один из них.

А 1.34. В круг вписан квадрат. Найти вероятность того, что точка, брошенная наудачу в круг, окажется внутри квадрата.

А 1.35. На шахматной доске случайным образом поставлены черная и белая ладьи. Какова вероятность того, что они не могут бить друг друга?

А 1.36. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.

А 1.37. На карточках отдельно написаны буквы: А – на 3;
Е – на 1-й; И – на 1-й; К – на 1-й; М – на 2; Т – на 2 карточках.
Ребенок берет карточки в случайном порядке и прикладывает их одну к другой. Найти вероятность того, что в результате получится слово «МАТЕМАТИКА».

А 1.38. 10 солдат-новобранцев разного роста случайным образом становятся в строй. Какова вероятность того, что они расположатся в строю по росту?

А 1.39. Среди поступающих в ремонт часов 40% нуждаются в общей чистке механизма. Какова вероятность того, что из 5 взятых наугад часов все нуждаются в чистке механизма?

А 1.40. Из 20 сбербанков 10 расположены за чертой города. Для аудиторской проверки случайно выбраны 5 сбербанков. Какова вероятность того, что хотя бы 2 из них окажутся в черте города?

Блок В

В 1.1. В механизм входят три одинаковые детали. Работа механизма нарушается, если при его сборке будут поставлены все три детали размера, больше обозначенного на чертеже. У сборщика пять деталей из оставшихся 12 большего размера. Найти вероятность: а) нормальной; б) ненормальной работы первого собранного из этих деталей механизма, если сборщик берет детали наудачу.

В 1.2. В механизм входят три одинаковые детали. Работа механизма нарушается, если при его сборке будут поставлены все три детали, большие или все три детали, меньшие обозначенного на чертеже размера. У сборщика осталось 15 деталей, из которых 10 по размеру больше, а остальные - меньше требуемого. Найти вероятность ненормальной работы первого собранного из этих деталей механизма, если сборщик берет детали наудачу.

В 1.3. При приеме партии изделий подвергается проверке половина изделий. Условие приемки - наличие брака в выборке не более 2%. Вычислить вероятность того, что партия из 100 изделий, содержащая 5% брака, будет принята.

В 1.4. Слово «ИНТЕГРАЛ» состоит из букв разрезной азбуки. Наудачу извлекают 4 карточки и выкладывают в ряд друг за другом в порядке появления. Какова вероятность того, что при этом получится слово «ИГРА»?

В 1.5. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы «А», «Г», «И», «Л», «М», «О», «Р», «Т», получится слово «АЛГОРИТМ»?

В 1.6. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы «О», «О», «О», «Л», «М», «Т», «К», получится слово «МОЛОТОК»?

В 1.7. Из пяти видов открыток наудачу выбираются 3 открытки. Какова вероятность того, что все три открытки будут разные?

В 1.8. На 5 одинаковых шарах написаны числа 1, 2, 3, 4, 5 – по одному на каждом. Шары положены в урну и перемешаны. Какова вероятность того, что, вынимая наудачу один за другим 3 шара, (без возврата) получим все 3 шара нечетного номера?

В 1.9. В группе учится 12 человек, из них 10 юношей и 2 девушки. На субботник отбирают 5 человек. Какова вероятность того, что в субботнике будут участвовать обе девушки?

В 1.10. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

В 1.11. Найти вероятность того, что точка, брошенная в произвольное место внутри круга радиуса R =5, попадет во вписанный в этот круг правильный треугольник.

В 1.12. Найти вероятность того, что точка, брошенная в произвольное место внутри круга радиуса R =6, попадет во вписанный в этот круг квадрат.

В 1.13. Найти вероятность того, что точка, брошенная в произвольное место внутри круга радиуса R =2, попадет во вписанный в этот круг прямоугольный равнобедренный треугольник.

В 1.14. В круг радиуса 10 см бросают точку. Найти вероятность того, что расстояние от этой точки до центра круга не превышает 5 см.

В 1.15. В круг радиуса 20 см бросают точку. Найти вероятность того, что расстояние от этой точки до центра круга больше 5 см.

В 1.16. В круг радиуса 12 см бросают точку. Найти вероятность того, что расстояние от этой точки до центра круга заключено в пределах от 2 до 5 см.

В 1.17. Стержень длиной 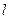разломали на две части. Найти вероятность того, что длина меньшей части не превысит .

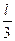В 1.18. Стержень длиной 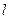разломали на две части. Найти вероятность того, что длина меньшей части превысит .

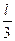Блок С

С 1 Наудачу выбраны два положительных числа 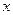и , каждое из которых не превышает 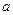. Найти вероятность того, что их сумма будет не больше 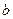, а отношение 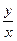– не меньше .

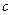Номер варианта	Исходные данные	Номер варианта	Исходные данные
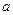
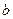
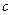
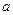
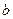
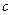
С 1.1				С 1.16			1/2
С 1.2				С 1.17
С 1.3			1/2	С 1.18
С 1.4				С 1.19			3/4
С 1.5			1/3	С 1.20			1/3
С 1.6				С 1.21
С 1.7				С 1.22
С 1.8				С 1.23
С 1.9				С 1.24
С 1.10			1/2	С 1.25
С 1.11			1/4	С 1.26			1/2
С 1.12				С 1.27			1/2
С 1.13				С 1.28			1/2
С 1.14				С 1.29
С 1.15				С 1.30

Дата добавления: 2014-11-18