Решение типовых задач. Повторные независимые испытания

Повторные независимые испытания

Тема 4

Здесь рассматриваются n последовательных независимых
испытаний, в каждом из которых событие 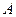может как произойти с постоянной вероятностью 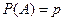, так и не произойти с вероятностью 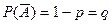. Результат испытаний –
появление события A 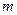раз ().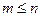

Задача 1. После года хранения на складе в среднем 10% аккумуляторов выходит из строя. Определить вероятность того, что после года хранения из 12 аккумуляторов окажутся годными: а) 10; б) больше половины.

Решение. Интересующее нас событие 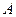– наудачу взятый аккумулятор после года хранения оказался годным, противоположное ему событие 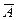– аккумулятор после года хранения вышел из строя. По условию 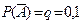, тогда .

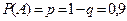а) Определим вероятность того, что из 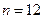аккумуляторов после года хранения на складе окажется годных 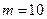. Применим формулу Бернулли .

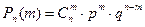Получаем .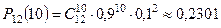

б) 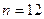; 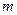может принять любое значение, большее 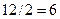, т. е. .

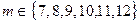Искомая вероятность 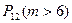найдется по теореме сложения и формуле Бернулли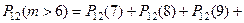

.

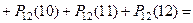
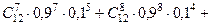
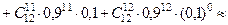
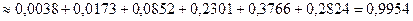Задача 2. Бракованные изделия, выпускаемые некоторым заводом, составляют в среднем 1,5%. Какое наивероятнейшее количество бракованных изделий будет в партии из 220 штук? Сколько нужно закупить изделий, чтобы наивероятнейшее число годных было равно 250?

Решение. Наивероятнейшее число успехов m ₀ в серии из 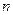испытаний при условии, что вероятность наступления интересующего нас события в каждом испытании постоянна и равна p, удовлетворяет следующему неравенству:

.

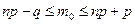Имеем 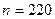(общее число изделий); 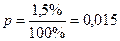(вероятность брака); 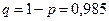(вероятность годного изделия).

Получим: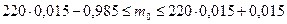

.

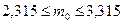Так как наивероятнейшее число бракованных изделий не может быть дробным числом, то единственным ответом будет .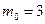

Определим, сколько нужно закупить изделий 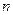, чтобы наивероятнейшее число годных было равно 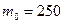. Здесь вероятность интересующего нас события (годного изделия) 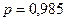, тогда :

,

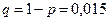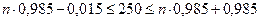или ; .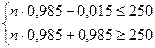

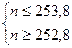Данной системе удовлетворяет единственное целое число n = 253.

Задача 3. Вероятность изготовления бракованной отливки равна 0,002. Определить вероятность того, что из выпущенных 500 отливок количество бракованных составит: а) 2; б) более двух.

Решение. В этой задаче значение n = 500 велико, вероятность p = 0,002 мала, произведение .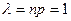

а) 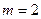. Найти вероятность 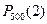можно по формуле Бернулли, но это нецелесообразно ввиду громоздкости вычислений. Воспользуемся формулой Пуассона

.

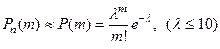Вероятность можно найти, воспользовавшись таблицей значений функции Пуассона (приложение В): P ₅₀₀(2)=0,1839.

б) 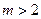, т.е. m = 3, 4, …, 500. Необходимо найти .

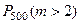Удобнее перейти к противоположному событию 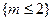, тогда .

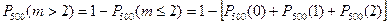Для вычисления каждого слагаемого 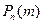используем формулу Пуассона пр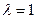и и .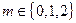

Получаем, пользуясь таблицей приложения В:

.

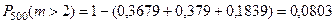Задача 4. Вероятность своевременного выполнения заказа цехами службы быта равна 0,75. Найти вероятность того, что из 160 заказов своевременно выполнят: а) 120; б) не менее 110.

Решение. Вероятность выполнения каждого заказа 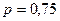; вероятность невыполнения .

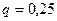а) 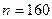велико, 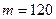; nрq ≥ 10. Для вычисления вероятности 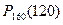воспользуемся локальной формулой Муавра-Лапласа , .

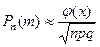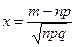Значения функции Гаусса 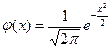находим по таблице (приложение А), учитывая ее четность .

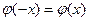Имеем .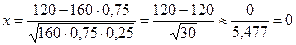

Тогда 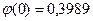. Искомая вероятность

.

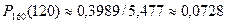б) 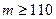, т.е. надо найти вероятность .

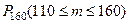Применим интегральную формулу Муавра-Лапласа

,

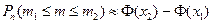где 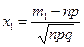, , 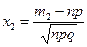а 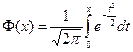– функция Лапласа (нечетная), значения которой приведены в приложении Б.

Вычисляем: ; .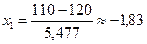

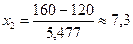По таблице находим

; .

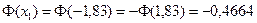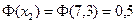Следовательно, искомая вероятность

.

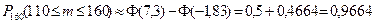Задача 5. При обработке линз в среднем 3 из 100 имеют брак. Сколько линз следует обработать, чтобы с вероятностью 0,95 можно было ожидать, что отклонение доли брака от его вероятности не превысит 0,01 (по абсолютной величине)?

Решение. Здесь p = 0,03 – вероятность линзе быть бракованной, тогда q = 1 – p = 0,97. Требуется найти число n при заданной надежности 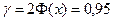. Воспользуемся следствием из интегральной теоремы Муавра-Лапласа, которое выражается формулой

,

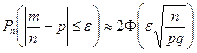где 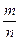– частота (доля) появления события А в независимых испытаниях. По условию задачи 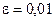, 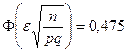. По таблице значений функции Лапласа, зная , находим 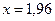. Тогда 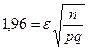, отсюда ,

.

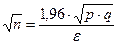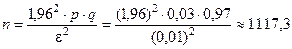Следовательно, нужно обработать 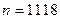линз, чтобы с вероятностью 0,95 можно было утверждать, что отклонение доли появления бракованной линзы от вероятности линзе быть бракованной (равной 0,03) не превосходит 0,01 (по абсолютной величине).

Дата добавления: 2014-11-18