
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальный закон распределения
|
|
|
|
Тема 7
Блок С
Блок В
Блок А
Задачи для отчета преподавателю
А 6.1. Случайная величина Х задана законом распределения
| xi | -3 | -1 | |||
| pi | 0,1 | 0,2 | 0,2 | 0,4 | 0,1 |
Найти функцию распределения этой случайной величины и
построить график. Определить аналитически и показать на графике 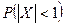 и
и  .
.
А 6.2. Снайпер стреляет до 1-го попадания. Вероятность промаха при одном выстреле равна р. Найти функцию распределения числа промахов.
А 6.3. Составить функцию распределения случайной величины, распределенной по биномиальному закону.
А 6.4. Среди поступающих в ОТК приборов 20% имеют отклонения от номинала. Найти функцию распределения числа точно собранных приборов среди 4, поступивших на контроль. Определить вероятность того, что число неточно собранных приборов
будет меньше 3.
А 6.5. Время ожидания троллейбуса распределено равномерно в интервале (0;5). Найти плотность вероятности времени ожидания, функцию распределения, среднее время ожидания и вероятность
того, что пассажир будет ждать троллейбус не более 3 мин.
А 6.6. Плотность распределения случайной величины Х задана формулой
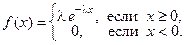
Построить график 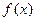 . Найти: а) функцию распределения; б) вероятность того, что случайная величина Х попадет в интервал
. Найти: а) функцию распределения; б) вероятность того, что случайная величина Х попадет в интервал
(-1; 2); в) математическое ожидание этой случайной величины.
А 6.7. Найти плотность вероятности и функцию распределения времени ожидания поезда метрополитена, зная, что оно равномерно распределено в интервале (0; 2). Вычислить математическое ожидание и дисперсию этой случайной величины.
В задачах А 6.8 – А 6.12 непрерывная случайная величина задана интегральной функцией 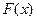 . Требуется найти: а) значение
. Требуется найти: а) значение
параметра 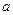 ; б) дифференциальную функцию
; б) дифференциальную функцию 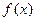 ; в) математическое ожидание и дисперсию случайной величины X; г) построить графики функций
; в) математическое ожидание и дисперсию случайной величины X; г) построить графики функций 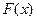 и
и 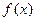 ; д) вероятность того, что случайная величина Х попадет в интервал (-1; 4).
; д) вероятность того, что случайная величина Х попадет в интервал (-1; 4).
А 6.8. 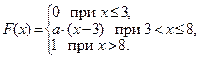
А 6.9. 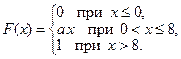
А 6.10. 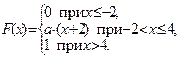 А 6.11.
А 6.11. 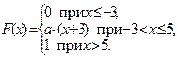
А 6.12. 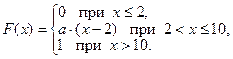
В задачах А 6.13 – А 6.20 величина Х задана функцией
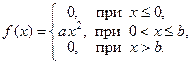
Требуется найти: а) значение параметра 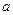 ; б) интегральную функцию
; б) интегральную функцию 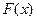 ; в)
; в) 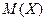 и
и 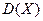 ; г) вероятность того, что 0 < Х < 1/3. Построить графики функций
; г) вероятность того, что 0 < Х < 1/3. Построить графики функций 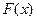 и
и 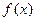 . Принять b равным:
. Принять b равным:
А 6.13. 1/2. А 6.14. 2/3. А 6.15. 3/2. А 6.16. 5/6.
А 6.17. 6/7. А 6.18. 7/8. А 6.19. 9/10. А 6.20. 10/11.
А 6.21. Брошены одновременно 2 игральные кости. Случайная величина Х принимает значение 1, если хотя бы на 1 игральной кости выпадает цифра 6; значение 2, если хотя бы на 1 из граней появилась четная цифра, но не 6; значение 0 – в остальных случаях. Написать функцию распределения этой случайной величины и найти ее математическое ожидание.
А 6.22. Из урны, содержащей 6 белых и 4 черных шара, случайным образом и без возвращения извлекают 3 шара. Составить функцию распределения случайной величины – числа черных шаров среди взятых. Найти математическое ожидание этой случайной величины.
А 6.23. Для сборки прибора требуется 4 однотипных деталей. Всего имеется 6 деталей, из которых только 5 доброкачественных. Составить функцию распределения случайной величины – числа доброкачественных деталей среди отобранных 4 деталей. Указать вероятность того, что можно будет произвести сборку прибора.
А 6.24. Случайная величина Х распределена по закону равнобедренного треугольника в интервале (-3; 3). Ее плотность вероятностей имеет вид, изображенный на рисунке. Найти F (x).

А 6.25. В театральной кассе осталось: 3 билета в драматический театр, 5 билетов в театр комедии, 1 билет в оперный театр и 1 билет в театр эстрады. Приобретение покупателем билета в любой из театров равновозможно. Составить закон распределения и найти функцию распределения числа билетов в драматический театр среди четырех билетов, купленных первыми.
А 6.26. Функция распределения величины Х имеет вид

Найти закон распределения случайной величины X, M (X) и D (X).
А 6.27. Случайная величина Х непрерывного типа может принимать ненулевые значения только на отрезке [-1; 1], причем функция распределения вероятностей имеет на этом отрезке зависимость 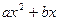 . Написать выражения функции распределения и плотности вероятностей на этом отрезке.
. Написать выражения функции распределения и плотности вероятностей на этом отрезке.
А 6.28. Случайная величина Х подчиняется закону распределения Парето с параметрами 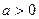 и
и 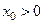 , если она есть случайная величина непрерывного типа и ее функция распределения
, если она есть случайная величина непрерывного типа и ее функция распределения
вероятностей имеет вид

Выяснить, при каких значениях параметра a для данного распределения существуют математическое ожидание и дисперсия, и
вычислить их.
А 6.29. Случайная величина Х задана законом распределения
| xi | ||||
| pi | 0,2 | 0,3 | 0,4 | ? |
Найти: а) вероятность 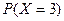 ; б) функцию распределения этой случайной величины. Построить график функции распределения. Определить аналитически и показать на графике
; б) функцию распределения этой случайной величины. Построить график функции распределения. Определить аналитически и показать на графике 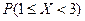 .
.
А 6.30. Стрелок стреляет по движущейся цели до первого попадания или до израсходования имеющихся 4 патронов. Составить функцию распределения числа израсходованных патронов, если вероятность попадания при каждом выстреле равна 0,6.
А 6.31. Среди отобранных часов 30% имеют отклонения в точности хода. Составить функцию распределения числа часов, не имеющих отклонений в точности хода среди трех наудачу взятых часов. Определить вероятность того, что количество таких часов не превышает 2.
А 6.32. Пусть случайная величина Х имеет 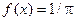 при
при 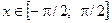 и
и 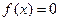 при
при 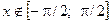 . Найти
. Найти
плотность случайной величины Y = sin X.
А 6.33. Плотность случайной величины Х 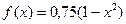 при х
при х 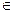 [-1;1] и f (х) = 0 при х
[-1;1] и f (х) = 0 при х  [-1;1]. Найти M (X) и D (X).
[-1;1]. Найти M (X) и D (X).
А 6.34. Функция распределения случайной величины Х

Найти М (Х) и D (X).
А 6.35. Случайная величина X имеет функцию распределения
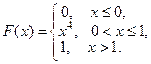
Найти математическое ожидание величины 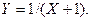
А 6.36. Показать, что функция
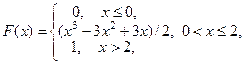
является функцией распределения некоторой случайной величины X. Найти вероятность Р (Х > 1) и M (X).
А 6.37. Плотность случайной величины X задана формулой
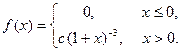
Найти константу с и М (Х).
А 6.38. Пусть F (х) – функция распределения случайной величины X. Найти функцию распределения случайной величины Y = аХ + b, а > 0.
А 6.39. Пусть величина Х имеет функцию распределения
F (x) = c 1 arctg x + c 2. Определить с 1 и с 2, найти 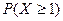 .
.
А 6.40. Пусть случайная величина Х имеет плотность 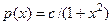 . Определить константу с и найти P (| X | < 1).
. Определить константу с и найти P (| X | < 1).
В 6.1. Найти функцию распределения числа попаданий в цель, если стрелком произведено шесть выстрелов, а вероятность попадания при одном выстреле равна 0,2. Пользуясь этой функцией, вычислить вероятность того, что цель будет поражена не менее одного, но менее пяти раз.
В 6.2. Дан закон распределения случайной величины Х. Составить ее функцию распределения. С помощью закона распределения и функции распределения рассчитать вероятность того, что случайная величина примет какое-нибудь значение, большее 1.
| Значение | – 2 | |||
| Вероятность | 0,1 | 0,5 | 0,3 | 0,1 |
В 6.3. Дан закон распределения случайной величины Х. Составить ее функцию распределения. С помощью закона распределения и функции распределения рассчитать вероятность того, что случайная величина примет какое-нибудь значение, меньшее 5.
| Значение | ||||
| Вероятность | 0,4 | 0,2 | 0,1 | 0,3 |
В 6.4. Дан закон распределения случайной величины Х. Составить ее функцию распределения. С помощью закона распределения и функции распределения рассчитать вероятность того, что случайная величина примет какое-нибудь значение, не меньшее 1.
| Значение | |||
| Вероятность | 0,5 | 0,25 | 0,25 |
В 6.5. Дан закон распределения случайной величины Х. Составить ее функцию распределения. С помощью закона распределения и функции распределения рассчитать вероятность того, что случайная величина примет какое-нибудь значение, большее 0.
| Значение | – 4 | ||
| Вероятность | 0,25 | 0,5 | 0,25 |
В 6.6. Дан закон распределения случайной величины Х. Составить ее функцию распределения. С помощью закона распределения и функции распределения рассчитать вероятность того, что случайная величина примет какое-нибудь значение, не большее 2.
| Значение | -1 | ||
| Вероятность | 0,2 | 0,3 | 0,5 |
В 6.7. Дан закон распределения случайной величины Х. Составить ее функцию распределения. С помощью закона распределения и функции распределения рассчитать вероятность того, что случайная величина примет какое-нибудь значение, меньшее 2.
| Значение | |||
| Вероятность | 0,1 | 0,3 | 0,6 |
В 6.8. Случайная величина Х равномерно распределена. Ее плотность вероятности 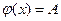 , если
, если 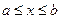 и
и  , если
, если  и
и  . Определить коэффициент А.
. Определить коэффициент А.
В 6.9. Найти математическое ожидание и дисперсию случайной величины, заданной плотностью вероятности 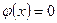 при
при 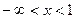 и
и 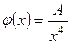 , если
, если 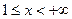 .
.
В 6.10. Найти математическое ожидание и дисперсию случайной величины, заданной плотностью вероятности 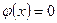 , если
, если 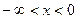 и
и  , если
, если  ;
; 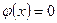 , если
, если 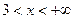 .
.
В 6.11. Найти математическое ожидание и дисперсию случайной величины, заданной плотностью вероятности 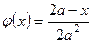 при
при 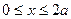 и
и 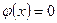 при
при 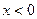 и
и  .
.
В 6.12. Случайная величина Х равномерно распределена. Плотность вероятности ее  при
при  и
и 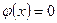 при
при  и
и  . Определить ее математическое ожидание и среднее квадратическое отклонение.
. Определить ее математическое ожидание и среднее квадратическое отклонение.
В 6.13. Функция 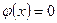 при
при 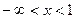 и
и 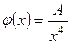 , если
, если 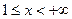 . Найти: а) значение А, при котором эта функция будет плотностью вероятности некоторой случайной величины Х; б) вероятность того, что в четырех независимых испытаниях она ни разу не попадет в интервал (1; 2).
. Найти: а) значение А, при котором эта функция будет плотностью вероятности некоторой случайной величины Х; б) вероятность того, что в четырех независимых испытаниях она ни разу не попадет в интервал (1; 2).
В 6.14. Функция 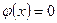 при
при 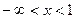 и
и  , если
, если 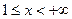 . Найти: а) функцию распределения этой случайной величины; б) вероятность того, что случайная величина Х примет какое-нибудь значение из интервала (2; 4).
. Найти: а) функцию распределения этой случайной величины; б) вероятность того, что случайная величина Х примет какое-нибудь значение из интервала (2; 4).
В 6.15. Функция 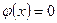 , если
, если 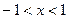 и
и 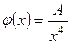 , если
, если 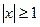 . Найти: а) значение А, при котором эта функция будет плотностью вероятности некоторой случайной величины; б) вероятность того, что эта случайная величина примет какое-нибудь значение, большее двух.
. Найти: а) значение А, при котором эта функция будет плотностью вероятности некоторой случайной величины; б) вероятность того, что эта случайная величина примет какое-нибудь значение, большее двух.
В 6.16. Функция 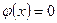 , если
, если 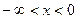 и
и  , если
, если  ;
; 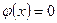 , если
, если 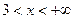 . Может ли эта функция быть плотностью вероятности некоторой случайной величины? Если да, то найти вероятность того, что эта случайная величина: а) примет значение из интервала (1; 2); б) в трех независимых испытаниях два раза окажется в интервале (1; 2).
. Может ли эта функция быть плотностью вероятности некоторой случайной величины? Если да, то найти вероятность того, что эта случайная величина: а) примет значение из интервала (1; 2); б) в трех независимых испытаниях два раза окажется в интервале (1; 2).
В 6.17. Плотность вероятности случайной величины Х 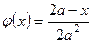 при
при 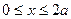 и
и 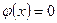 при
при 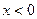 и
и  . Найти ее функцию распределения, построить графики
. Найти ее функцию распределения, построить графики  и функции распределения.
и функции распределения.
В 6.18. Случайная величина задана функцией распределения:
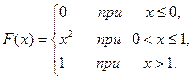
Найти вероятность того, что в результате четырех независимых испытаний случайная величина Х ровно три раза примет значение из интервала (0,25; 0,75).
В 6.19. Случайная величина Х задана плотностью вероятности 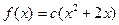 в интервале (0; 1), за пределами этого интервала
в интервале (0; 1), за пределами этого интервала 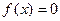 . Найти: а) параметр с; б) математическое ожидание величины Х.
. Найти: а) параметр с; б) математическое ожидание величины Х.
С 7 Задан закон распределения случайной величины 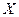 в виде таблицы. Необходимо:
в виде таблицы. Необходимо:
а) построить многоугольник распределения вероятностей;
б) найти аналитическое выражение для функции распределения и построить ее график;
в) найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
| С 7.1 | X | -2 | С 7.2 | X | -1 | |||||||||
| P | 0,2 | 0,1 | 0,3 | 0,3 | 0,1 | P | 0,2 | 0,1 | 0,3 | 0,2 | 0,2 |
| С 7.3 | X | С 7.4 | X | -2 | ||||||||||
| P | 0,1 | 0,2 | 0,1 | 0,4 | 0,2 | P | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
| С 7.5 | X | С 7.6 | X | -3 | ||||||||||
| P | 0,1 | 0,3 | 0,1 | 0,4 | 0,1 | P | 0,2 | 0,1 | 0,3 | 0,2 | 0,2 |
| С 7.7 | X | С 7.8 | X | |||||||||||
| P | 0,2 | 0,1 | 0,3 | 0,3 | 0,1 | P | 0,1 | 0,3 | 0,2 | 0,3 | 0,1 |
| С 7.9 | X | С 7.10 | X | -2 | ||||||||||
| P | 0,1 | 0,3 | 0,1 | 0,4 | 0,1 | P | 0,2 | 0,1 | 0,3 | 0,3 | 0,1 |
| С 7.11 | X | С 7.12 | X | -3 | -1 | |||||||||
| P | 0,2 | 0,1 | 0,3 | 0,2 | 0,2 | P | 0,3 | 0,1 | 0,2 | 0,1 | 0,3 |
| С 7.13 | X | -3 | С 7.14 | X | ||||||||||
| P | 0,2 | 0,1 | 0,4 | 0,2 | 0,1 | P | 0,3 | 0,1 | 0,4 | 0,1 | 0,1 |
| С 7.15 | X | С 7.16 | X | -4 | -1 | |||||||||
| P | 0,1 | 0,3 | 0,4 | 0,1 | 0,1 | P | 0,2 | 0,1 | 0,3 | 0,1 | 0,3 |
| С 7.17 | X | -5 | С 7.18 | X | ||||||||||
| P | 0,2 | 0,1 | 0,4 | 0,1 | 0,2 | P | 0,2 | 0,1 | 0,4 | 0,1 | 0,2 |
| С 7.19 | X | С 7.20 | X | -5 | -2 | |||||||||
| P | 0,1 | 0,3 | 0,2 | 0,3 | 0,1 | P | 0,1 | 0,3 | 0,2 | 0,3 | 0,1 |
| С 7.21 | X | -3 | С 7.22 | X | ||||||||||
| P | 0,1 | 0,3 | 0,2 | 0,3 | 0,1 | P | 0,3 | 0,1 | 0,2 | 0,1 | 0,3 |
| С 7.23 | X | С 7.24 | X | -2 | ||||||||||
| P | 0,2 | 0,1 | 0,4 | 0,1 | 0,2 | P | 0,2 | 0,1 | 0,3 | 0,3 | 0,1 |
| С 7.25 | X | -3 | С 7.26 | X | ||||||||||
| P | 0,1 | 0,3 | 0,2 | 0,3 | 0,1 | P | 0,2 | 0,1 | 0,2 | 0,3 | 0,2 |
| С 7.27 | X | -6 | -3 | С 7.28 | X | -3 | ||||||||
| P | 0,2 | 0,3 | 0,1 | 0,2 | 0,2 | P | 0,2 | 0,1 | 0,4 | 0,1 | 0,2 |
| С 7.29 | X | С 7.30 | X | -4 | -1 | |||||||||
| P | 0,2 | 0,2 | 0,1 | 0,2 | 0,3 | P | 0,3 | 0,1 | 0,1 | 0,3 | 0,2 |
С 8 Непрерывная случайная величина задана функцией распределения 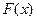 . Необходимо найти:
. Необходимо найти:
а) вероятность попадания случайной величины в интервал 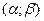 ;
;
б) плотность распределения случайной величины 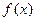 ;
;
в) математическое ожидание 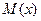 , дисперсию
, дисперсию 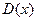 и среднее квадратическое отклонение
и среднее квадратическое отклонение 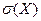 .
.
Построить графики функций 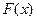 и
и 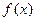 .
.
С 8.1 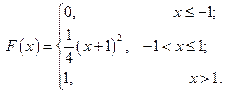
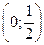 С 8.2
С 8.2 
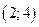
С 8.3 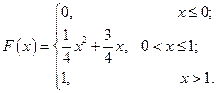
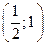
С 8.4 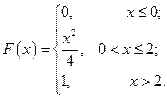
С 8.5 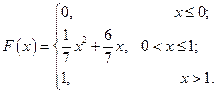
С 8.6 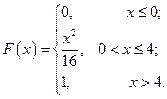
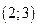
С 8.7 
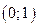
С 8.8 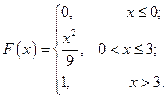
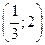
С 8.9 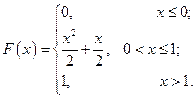

С 8.10 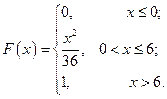
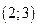
С 8.11 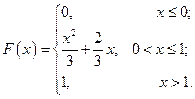
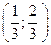
С 8.12 
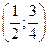
С 8.13 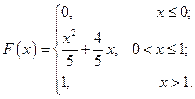
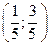
С 8.14 

С 8.15 
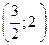
С 8.16 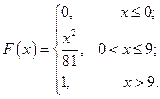
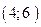
С 8.17 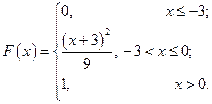
С 8.18 
С 8.19 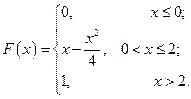
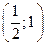
С 8.20 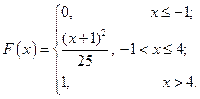
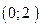
С 8.21 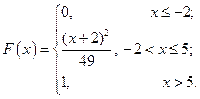
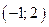
С 8.22 
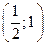
С 8.23 
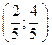
С 8.24 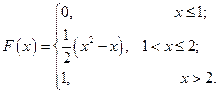
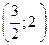
С 8.25 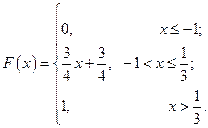
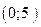
С 8.26 
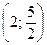
С 8.27 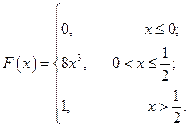
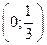
С 8.28 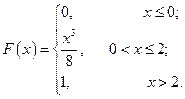
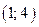
С 8.29 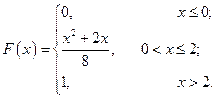

С 8.30 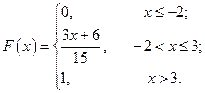
Случайная величина X называется распределенной по нормальному закону, если ее плотность f (х) имеет вид
 .
.
Здесь 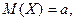
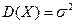 . В этом случае пишут X ~ N
. В этом случае пишут X ~ N 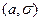 , где
, где  – среднее квадратическое отклонение.
– среднее квадратическое отклонение.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 2001; Нарушение авторских прав?; Мы поможем в написании вашей работы!