Решение типовых задач. Задача 1. При сортировке случайные значения веса зерна распределены нормально со средним значением 0,15 г и средним квадратическим отклонением 0,03 г

Задача 1. При сортировке случайные значения веса зерна распределены нормально со средним значением 0,15 г и средним квадратическим отклонением 0,03 г. Нормальные всходы дают зерна, вес которых более 0,10 г. Определить: а) процент семян, от которых следует ожидать нормальные всходы; б) величину, которую не превзойдет вес отдельного зерна с вероятностью 0,99.

Решение. Обозначим Х – случайный вес зерна. По условию

,

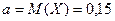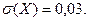
а) Процент семян, дающих нормальные всходы – это вероятность того, что взятое наугад зерно нормально взойдет. По условию нормальные всходы дают зерна, удовлетворяющие условию Х > 0,10.

Вероятность этого события найдем по формуле

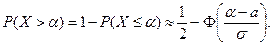
Подставляя числовые значения, получаем

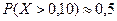
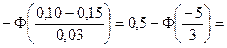
т. е. от 95,2% семян следует ожидать нормальных всходов.

б) Обозначим искомую величину веса через . Воспользу­емся для ее нахождения формулой .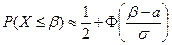

Находим из условия или

; .

По таблице значений функции 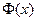находим 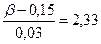, откуда 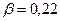. Таким образом, вес взятого наугад зерна не будет превышать 0,22 г с вероятностью 0,99.

Задача 2. Случайные отклонения диаметра детали, выпускаемой цехом, от номинала распределены нормально. Математическое ожидание диаметра детали равно 20 мм, а дисперсия 0,36 мм. Найти:

1) вероятность того, что диаметр наудачу взятой детали: а) имеет размеры от 19 до 22 мм; б) отличается от математического значения не более чем на 1 мм (по абсолютной величине);

2) границы, в которых следует ожидать величину диаметра детали, чтобы вероятность невыхода за эти границы была равна 0,9876.

Решение. Обозначим Х – величина диаметра детали. По условию , , тогда .

1.а) Найдем вероятность , для чего воспользуемся формулой

.

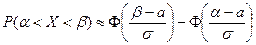Получаем

.

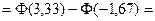
1.б) Найдем вероятность 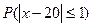. Имеем

или .

2) По условию 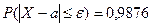. По таблице значений 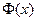находим 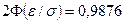значит, , отсюда .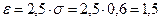

Диаметр детали X удовлетворяет неравенству 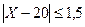. Отсюда находим или , т.е. с вероятностью 0,9876.

Задача 3. Результат взвешивания химреактива распределен по нормальному закону со средним квадратическим отклонением веса г. Какое отклонение массы реактива можно гарантировать с вероятностью 0,2?

Решение. В условии задачи дано, что 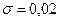, , 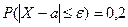где . Нужно найти .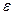

Воспользуемся формулой .

Согласно условию задачи . По таблице значений функции Лапласа 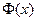имеем .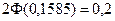

Значит, , откуда 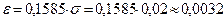. Итак, с вероятностью 0,2 можно ожидать отклонения массы реактива, равного 0,0032 г.

Дата добавления: 2014-11-18