Дискретная случайная величина

Тема 5

Блок С

Блок В

Блок А

Задачи для отчета преподавателю

А 4.1. При установившемся технологическом процессе автомат производит 75% числа деталей 1-го сорта и 25% – 2-го сорта.
Установить, что является более вероятным – получить 3 первосортных детали среди 5 наудачу отобранных или 4 первосортных среди 6 наудачу отобранных?

А 4.2. Сколько раз надо подбрасывать монету, чтобы вероятность того, что герб выпадет 3 раза, равнялась 0,25?

А 4.3. Вероятность выигрыша по билету равна 0,2. Сколько нужно приобрести билетов, чтобы с вероятностью не меньшей 0,9 среди них был хотя бы один выигрышный?

А 4.4. Среди изделий, произведенных на станке-автомате, в среднем бывает 90% изделий 1-го сорта. Какова вероятность того, что среди 5 наудачу выбранных изделий будет не менее 4 изделий 1-го сорта?

А 4.5. Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди 8 случайно отобранных волокон смеси обнаружить менее 4 окрашенных?

А 4.6. Что вероятнее, выиграть у равносильного противника не менее 3 партий из 4 или не менее 5 из 8?

А 4.7. Среди изделий, изготовленных вручную, бывает в среднем 4% брака. Какова вероятность того, что среди взятых наудачу 5 изделий будет 40% бракованных?

А 4.8. Каждый из 4 станков в течение 6 часов работы останавливается несколько раз и всего в сумме простаивает 1 ч., причем остановка его в любой момент времени равновероятна. Найти вероятность того, что в данный момент времени будут работать два станка.

А 4.9. При сборке в среднем 2% механизмов оказываются с дефектами. Контроллер проверяет взятые наудачу 6 механизмов. Определить вероятность того, что среди них с дефектами окажется не более 1 механизма.

А 4.10. В автобусном парке ежедневно выходит на линию 100 автобусов. Вероятность выхода из строя двигателя у одного автобуса равна 0,1. Определить вероятность того, что в течение дня выйдут из строя не более чем 2 двигателя.

А 4.11. Вероятность прорастания зерна равна 0,8. Определить наивероятнейшее число зерен, которые прорастут из 400 зерен, и вероятность этого события.

А 4.12. При данном технологическом процессе 80% всей продукции оказывается продукцией высшего сорта. Определить наивероятнейшее число изделий высшего сорта в партии из 200 изделий и его вероятность.

А 4.13. В результате проверки качества приготовленного для посева зерна было установлено, что 80% зерен всхожие.
Определить вероятность того, что среди отобранных и высаженных 100 зерен прорастет не менее 70.

А 4.14. Вероятность того, что пара обуви, взятая наудачу из изготовленной партии, окажется 1-го сорта, равна 0,7. Определить вероятность того, что среди 2100 пар, поступающих на контроль, число пар первосортной обуви окажется не менее 1000 и
не более 1500.

А 4.15. Наиболее вероятная частота появления события при независимых испытаниях равна 50, а дисперсия – 25. Оценить абсолютную величину отклонения частоты появления события от вероятности её появления с вероятностью 0,9973.

А 4.16. Вероятность рождения мальчика р = 0,515. Какова вероят­ность того, что из 1000 родившихся детей мальчиков будет 520?

А 4.17. В ОТК с конвейера для проверки поступила партия изделий в количестве 600 штук. Какова вероятность того, что среди этих изделий имеется 500 изделий 1-го сорта, если известно, что с конвейера в среднем поступает 85% продукции 1-го сорта?

А 4.18. Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице будет не менее 3 опечаток.

А 4.19. Вероятность изготовления бракованного изделия равна 0,001. Вычислить вероятность того, что в партии из 200 изделий число бракованных более 2.

А 4.20. Вероятность изготовления консервной банки с недостаточной герметизацией равна 0,02. Среди скольких банок, отобранных случайным образом, можно с вероятностью 0,9 ожидать отсутствия бракованных?

А 4.21. Всхожесть семян некоторого растения составляет 70%. Какова вероятность того, что из 100 семян взойдет не менее 80?

А 4.22. Вероятность того, что пара обуви, взятая наудачу из изго­товленной партии, окажется 1-го сорта, равна 0,8. Найти вероят­ность того, что среди 1800 пар, поступающих на контроль, число пар первосортной обуви окажется не менее 1400 и не более 1460.

А 4.23. Коэффициент простоя станка в среднем равен 0,1. В цехе имеется 12 таких станков. Какова вероятность того, что в некоторый момент времени при нормальном процессе производства 8 из 12 станков будут работать?

А 4.24. Каждый житель некоторого поселка 5 раз в месяц выезжает в город. Считая, что выбор дня для поездки случаен, определить, сколько вагонов должно быть в электричке, чтобы она переполнялась не чаще 1 раза в 100 дней. Число мест в одном вагоне принять равным 60, а число жителей поселка 3600.

А 4.25. Автоматическая штамповка клемм для предохранителей дает 10% отклонений от принятого стандарта. Сколько клемм необходимо взять наудачу, чтобы вероятность того, что среди них число стандартных отличается от среднего значения такого числа (по модулю) меньше чем на 10, была равна 0,9586?

А 4.26. По данным длительной проверки качества выпускаемых запчастей определенного вида брак составляет 13%. Найти вероятность того, что в непроверенной партии из 150 запчастей пригодных будет 128 штук.

А 4.27. Подлежат исследованию 400 проб руды. Вероятность
того, что промышленное содержание железа в каждой пробе выше 50%, равна 0,8. Найти вероятность того, что среди них число проб руды с промышленным содержанием свыше 50% не менее 300.

А 4.28. Вероятность того, что наугад взятое изделие окажется пригодным без доводки, равна 0,9. Сколько изделий нужно отобрать, чтобы с вероятностью 0,9545 можно было утверждать, что доля пригодных без доводки изделий среди них отклонится по абсолютной величине от 0,9 не более чем на 0,05?

А 4.29. Производятся 5 выстрелов по мишени с вероятностью попа­дания при каждом выстреле 0,3. Для поражения мишени достаточно 3 попаданий. Найти вероятность того, что мишень будет поражена.

А 4.30. При обработке некоторой детали наблюдается в среднем 5% нарушений норм ее установленных размеров. Установить необходимое количество деталей, подлежащих обработке, чтобы ожидать с вероятностью 0,9 отклонение частости появления неточ­ных деталей от вероятности этого события не более чем на 0,02.

А 4.31. Вероятность попадания при одном выстреле равна 0,7. Найти вероятность того, что из 5 выстрелов будет хотя бы 1 попадание.

А 4.32. Вероятность сбора 45 ц хлопка с 1 га равна 0,7. Вычислить вероятность сбора хлопка по 45 ц с га не менее чем с 4 га.

А 4.33. Среди студентов 60% учатся на "хорошо" и "отлично". Найти вероятность того, что среди 400 случайно опрошенных студентов не менее 350 учатся на "хорошо" и "отлично".

А 4.34. Процент всхожести семян кукурузы равен 95%. Найти вероятность того, что из 2000 посеянных семян число не взошедших будет от 80 до 120 (включительно).

А 4.35. На склад поступает продукция с 3 фабрик, доля которых составляет соответственно 30%, 32%, 38%. В продукции 1-й фабрики 60% изделий высшего сорта, второй – 50%, третьей – 40%. Найти вероятность того, что среди 300 наудачу взятых изделий число изделий высшего сорта заключено между 150 и 200.

А 4.36. Вероятность того, что в пути изделие повредится, равна 0,005. С какой вероятностью можно ожидать не менее 5 поврежденных изделий среди 1000 отправленных?

А 4.37. Вероятность банкротства одной из 6 фирм к концу года равна р = 0,2. Какова вероятность того, что к концу года обанкротится не более двух фирм?

А 4.38. В порту каждые сутки может появиться одно большегруз­ное судно с вероятностью . Вероятность появления более одного судна в течение суток пренебрежимо мала. Какова вероят­ность того, что за месяц (30 дней) порт посетят не более 4 судов?

А 4.39. Телефонная станция обслуживает 600 абонентов. Вероят­ность любого из них позвонить в течение часа равна 0,005. Найти наиболее вероятное число звонков в течение часа и его вероятность.

А 4.40. При наборе слова оператор делает ошибку с вероятностью 0,002. Какова вероятность, что в набранной статье, состоящей из 3000 слов, будет не более 4 ошибок?

В 4.1. Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность того, что лицо, имеющее шесть билетов: а) выиграет по двум билетам; б) выиграет по трем билетам; в) не выиграет по двум билетам?

В 4.2. Принимая вероятности рождения мальчика и девочки одинаковыми, найти вероятность того, что среди 10 новорожденных шесть окажутся мальчиками.

В 4.3. На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой из них равна 0,8. Найти вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не менее восьми автомашин.

В 4.4. Всхожесть семян некоторого растения составляет 70%. Какова вероятность того, что из 10 посеянных семян взойдут: а) восемь; б) по крайней мере восемь; в) не менее трех?

В 4.5. Пусть вероятность того, что наудачу взятая деталь нестандартная, равна 0,1. Найти вероятность того, что среди взятых наудачу пяти деталей не более двух окажутся нестандартными.

В 4.6. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из
пяти первых покупателей обувь этого размера будет необходима: а) одному; б) по крайней мере одному.

В 4.7. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из шести телевизоров: а) не более одного потребует ремонта; б) хотя бы один потребует
ремонта.

В 4.8. Вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что среди 10 деталей окажется не более одной нестандартной?

В 4.9. Вероятность производства бракованной детали равна 0,008. Найти наивероятнейшее число бракованных среди
1000 деталей и вероятность такого количества их в партии.

В 4.10. Пусть вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найти наиболее вероятное число опоздавших из 855 пассажиров.

В 4.11. Пусть вероятность того, что денежный автомат при опускании одной монеты сработает неправильно, равна 0,03.
Найти наивероятнейшее число случаев правильной работы автомата, если будет опущено 150 монет.

В 4.12. Оптовая база обслуживает 12 магазинов. От каждого из них заявка на товары на следующий день может поступить с вероятностью 0,3. Найти наивероятнейшее число заявок на следующий день и вероятность получения базой такого числа заявок.

В 4.13. Вероятность того, что денежный автомат при опускании одной монеты сработает правильно, равна 0,97. Сколько нужно опустить монет, чтобы наивероятнейшее число случаев
правильной работы автомата было равно 100?

В 4.14. Сколько нужно взять деталей, чтобы наивероятнейшее число годных было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1?

В 4.15. Пусть вероятность нарушения герметичности банки консервов равна 0,0005. Найти вероятность того, что среди
2000 банок две окажутся с нарушением герметичности.

В 4.16. Вероятность попадания в цель при одном выстреле
равна 0,4. Найти вероятность 100 попаданий из 320 выстрелов.

В 4.17. Найти вероятность того, что из 500 посеянных семян не взойдет 130, если всхожесть семян оценивается вероятностью 0,75.

В 4.18. Вероятность рождения мальчика равна 0,515. Какова вероятность того, что среди 1000 новорожденных будет 480 девочек?

В 4.19. Вероятность наступления события в каждом испытании равна 0,8. Найти наибольшее отклонение частости этого события от вероятности его наступления, которое можно ожидать с вероятностью 0,9127 при 4900 испытаниях.

В 4.20. Мастерская по гарантийному ремонту телевизоров обслуживает 2000 абонентов. Вероятность того, что купленный телевизор потребует гарантийного ремонта, равна 0,3. Предполагая, что событие, вероятность которого 0,9973, достоверно, найти границы числа телевизоров, которые потребуют гарантийного ремонта.

В 4.21. На прядильной фабрике работница обслуживает 750 веретен. При вращении веретена пряжа рвется в случайные моменты времени из-за неравномерности натяжения, неровности и других причин. Считая, что вероятность обрыва пряжи на каждом из веретен в течение некоторого промежутка времени t равна 0,008, найти вероятность того, что за это время произойдет не более 10 обрывов.

В 4.22. При штамповке металлических клемм получается в среднем 90% годных. Найти вероятность того, что среди 900 клемм будет от 790 до 820 (включительно) годных.

В 4.23. Вероятность неточной сборки прибора равна 0,2. Найти вероятность того, что среди 500 приборов окажется от 410 до 430 (включительно) точных.

В 4.24. Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из 800 посеянных семян взойдет не менее 700.

В 4.25. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из 750 покупателей не более 120 потребуют обувь этого размера.

В 4.26. Предприятие имеет 2400 агрегатов. В каждый агрегат входит некоторая деталь, вероятность выхода из строя которой за время t равна 1/6. Исходя из этого отдел снабжения заготовил на время t 400 запасных деталей этого типа. Найти вероятность того, что это количество запасных деталей обеспечит бесперебойную работу всех агрегатов в течение времени t.

В 4.27. Вероятность поражения мишени при одном выстреле равна 0,6. Найти: а) границы числа попаданий в мишень при 600 выстрелах, чтобы вероятность невыхода за эти границы была равна 0,993; б) такое число выстрелов по мишени, при котором с вероятностью 0,993 можно ожидать, что отклонение частости попаданий от вероятности 0,6 не превзойдет 0,03 (по абсолютной величине).

В 4.28. Вероятность того, что покупателю необходима мужская обувь 41-го размера, равна 0,2. Если будет 10 000 покупателей, то: а) какова вероятность того, что доля тех, кому необходима обувь этого размера, отклонится от вероятности 0,2 не более чем на 0,005 (по абсолютной величине); б) какое с вероятностью 0,9973 можно ожидать наибольшее отклонение от вероятности 0,2 доли тех покупателей, которым необходима обувь 41-го размера?

В 4.29. Вероятность промышленного содержания металла в каждой пробе руды равна 0,4. Принимая, что событие, вероятность которого 0,997, достоверно, найти границы числа проб с промышленным содержанием металла среди 1000 проб.

В 4.30. Сколько нужно проверить деталей, чтобы с вероятностью: а) 0,9; б) 0,99; в) 0,999 можно было ожидать, что абсолютная величина отклонения частости годных деталей от вероятности 0,9 того, что деталь будет годной, не превысит 0,01 (по абсолютной величине)?

С 4а Импортер поставляет жалюзи для окон, причем из них 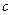% горизонтальных. Какая вероятность того, что среди 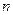отобранных жалюзи будет: а) m горизонтальных; б) от m ₁ до m ₂ горизонтальных; в) не меньше m ₃ горизонтальных; г) меньше m ₄ горизонтальных?

Номер варианта	Исходные данные
%
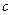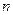
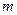
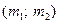
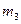
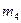
С 4.1			–	–		–
С 4.2			–	3; 5	–	–
С 4.3				–	–	–
С 4.4			–	–	–
С 4.5			–	3; 4	–	–
С 4.6				–	–	–
С 4.7			–	–		–
С 4.8				–	–	–
С 4.9			–	–	–
С 4.10				–	–	–
С 4.11			–	–		–
С 4.12			–	2; 4	–	–
С 4.13				–	–	–
С 4.14			–	–		–
С 4.15			–	–	–
С 4.16			–	2; 5	–	–
С 4.17			–	2; 3	–	–
С 4.18			–	3; 4	–	–
С 4.19			–	3; 4	–	–
Номер варианта	Исходные данные
%
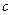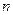
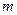
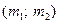
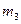
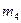
С 4.20				–	–	–
С 4.21			–	–	–
С 4.22			–	–		–
С 4.23				–	–	–
С 4.24			–	3; 4	–	–
С 4.25			–	–	–
С 4.26				–	–	–
С 4.27			–	–		–
С 4.28			–	3; 4	–	–
С 4.29				–	–	–
С 4.30			–	–	–

С 5а Вероятность того, что покупатель закажет товар фирмы "Faberlic", равна 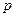. Найти вероятность того, что среди 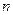покупателей таких будет: а) k; б) не меньше k ₁; в) от k ₂ до k ₃; г) меньше k ₄.

Номер варианта	Исходные данные
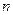
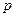
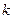
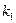
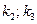
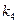
		0,3		–	–
		0,2		–	500; 600	–
		0,3			–	–
		0,4			–	–
		0,25		–	400; 550	–
		0,35		–	–
		0,25		–	550; 650	–
		0,3			–	–
		0,25			–	–
		0,3		–	–
		0,3		–	650; 750	–
		0,3			–	–
		0,2		–	–
		0,4		–	900; 950	–

С 5б Вероятность того, что покупатель закажет товар фирмы "Oriflame", равна 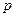. Найти вероятность того, что среди 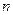покупателей отклонение доли покупателей, которые желают заказать продукцию, от вероятности 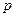не превышает .

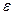Номер варианта	Исходные данные
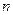
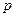
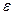
		0,35	0,03
		0,4	0,02
		0,4	0,03
		0,3	0,01
		0,4	0,02
		0,3	0,03
		0,4	0,02
		0,45	0,01

С 5в Вероятность того, что каждому из 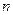покупателей необходим товар фирмы "Avon", равна 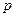. Найти границы, в которых с вероятностью 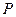будет находиться доля покупателей, которые желают заказать продукцию фирмы.

Номер варианта	Исходные данные
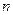
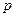
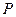
		0,3	0,9729
		0,4	0,9606
		0,4	0,9791
		0,3	0,9556
		0,3	0,9807
		0,4	0,9616
		0,3	0,9774
		0,4	0,9596

С 6 Найти вероятность того, что среди изготовленных 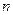деталей окажется 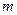деталей с дефектом, если вероятность изготовления детали с дефектом равна .

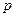Номер варианта	Исходные данные	Номер варианта	Исходные данные
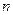
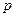
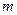
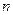
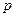
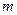
		0,005				0,005
		0,003				0,001
		0,004				0,0002
		0,0005				0,001
		0,0004				0,001
		0,005				0,001
		0,0005				0,0005
		0,005				0,0006
		0,004				0,0008
		0,0003				0,002
		0,005				0,003
		0,0001				0,0002
		0,0002				0,004
		0,0001				0,0004
		0,006				0,0001

Понятие дискретной случайной величины тесно связано с
понятием случайного события, являясь в некотором смысле его обобщением. Здесь также первичным служит испытание,
результат которого характеризуется не альтернативным исходом (появляется или нет событие), а некоторым числом (число m
появлений события А в n повторных независимых испытаниях: число очков, выбиваемых стрелком; размер вклада на случайно выбранном в сбербанке счете и т.д.).

Связь со случайным событием заключается в том, что принятие случайной величиной некоторого числового значения
(т.е. выполнение равенства ) есть случайное событие,
характеризуемое вероятностью .

Дата добавления: 2014-11-18