Задачи для отчета преподавателю. А 2.1.Из урны, содержащей 5 синих, 3 черных, 2 белых шара, извлекаются одновременно 3 шара

Блок А

А 2.1. Из урны, содержащей 5 синих, 3 черных, 2 белых шара, извлекаются одновременно 3 шара. Найти вероятность того, что извлеченные шары будут разных цветов.

А 2.2. Вероятность того, что в электрической цепи напряжение превысит номинальное значение, равна 0,1. При повышенном напряжении вероятность аварии прибора потребителя электрического тока равна 0,08. Найти вероятность аварии прибора в случае повышения напряжения.

А 2.3. Каждая буква слова "математика" написана на отдельной карточке. Случайно извлекаются 4 карточки. Какова вероятность получить при этом слово "тема"?

А 2.4. Номер серии выигрышного билета лотереи состоит из 5 цифр. Найти вероятности того, что 1-й номер выигравшей серии будет состоять только из нечетных цифр.

А 2.5. Условиями приема допускается число бракованных деталей не более 1 детали из 5. Найти вероятность того, что партия из 10 деталей, среди которых 3 бракованных, будет принята при испытании выбранной наудачу половины всей партии.

А 2.6. Какова вероятность того, что выбранное наудачу изделие окажется первосортным, если известно, что 3% всей продукции составляют нестандартные изделия, а 75% стандартных изделий удовлетворяют требованиям 1-го сорта?

А 2.7. Вероятность только одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели 1-м орудием, если для 2-го эта вероятность равна 0,8.

А 2.8. Рабочий обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что в течение часа 1-й станок не потребует внимания рабочего, равна 0,9; для 2-го – 0,8; для третьего – 0,85. Какова вероятность того, что в течение часа потребуют внимания рабочего: а) ни один станок; б) все три станка; в) какой-нибудь один станок; г) хотя бы один станок?

А 2.9. Агрегат имеет 3 двигателя и способен функционировать, если работают по крайней мере 2 из них. Вероятность выхода из строя 1-го двигателя – 0,01; 2-го – 0,02; 3-го – 0,03. Какова вероятность выхода из строя агрегата?

А 2.10. Из урны, содержащей 6 белых и 4 черных шаров,
наудачу и последовательно извлекают по 1 шару до появления черного шара. Найти вероятность того, что придется производить четвертое извлечение, если выборка производится: а) с возвращением; б) без возвращения.

А 2.11. Студент может уехать в институт или автобусом, который ходит через каждые 20 минут, или троллейбусом, который
ходит через каждые 10 минут. Какова вероятность того, что студент, подошедший к остановке, уедет в течение: а) ближайших 5 минут; б) ближайших 10 минут?

А 2.12. Радист трижды вызывает корреспондентов. Вероятность того, что корреспондент примет 1-й вызов, равна 0,2; 2-й – 0,3 и 3-й – 0,4. По условиям приема события, состоящие в том, что i -й по счету вызов
(i = 1, 2, 3) услышан, независимы. Найти вероятность того, что корреспондент: а) услышит радиста; б) не услышит радиста.

А 2.13. В театральной кассе к некоторому моменту времени остались: 1 билет в театр эстрады, 2 билета в драматический театр и 3 билета в театр комедии. Каждый очередной покупатель приобретает лишь один билет в любой из возможных театров. Два человека из очереди последовательно приобрели билеты. Найти вероятность того, что: а) куплены билеты в разные театры; б) куплены билеты в один какой-нибудь театр; в) все билеты в театр эстрады распроданы; г) билет в театр комедии куплен раньше, чем в театр эстрады.

А 2.14. Студенты выполняют контрольную работу в классе контролирующих машин. Работа состоит из 3 задач. Для получения положительной оценки достаточно решить 2 задачи. Для каждой задачи зашифровано 5 различных ответов, из которых только один правильный. Студент плохо знает материал и поэтому выбирает ответы для каждой задачи наудачу. Какова вероятность того, что он получит положительную оценку?

А 2.15. Наудачу подбрасывают 2 игральные кости. Найти вероятность того, что: а) сумма выпавших очков четна; б) произ­ведение очков четно; в) на одной из костей число очков четно, а на другой нечетно; г) ни на одной из костей не выпало 6 очков.

А 2.16. Вероятность улучшить свой прежний результат для данного спортсмена равна р. Найти вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать 2 попытки.

А 2.17. Абонент забыл последнюю цифру номера телефона, поэтому набирает ее наудачу. Определить вероятность того, что ему придется звонить не более чем в 3 места. Как изменится вероятность, если он помнит, что эта цифра нечетная?

А 2.18. Технический контроль проверяет из партии готовой продукции не более 5 изделий последовательно друг за другом. При обнаружении бракованного изделия бракуется вся партия. Найти вероятность того, что вся партия будет забракована, если брак в ней составляет 4%.

А 2.19. Вероятность попадания в цель при 1 выстреле равна 1/2. Найти вероятность того, что с 2 выстрелов цель будет поражена.

А 2.20. В механизм входят 2 одинаковые детали. Механизм не будет работать тогда, когда обе поставленные детали будут уменьшенного размера. У сборщика 10 деталей, из них 3 меньше стандарта. Найти вероятность того, что механизм будет работать, если детали извлекаются случайно.

А 2.21. Вероятность того, что в страховую компанию в течение года обратится с иском о возмещении ущерба 1-й клиент,
равна 0,15. Для 2-го клиента вероятность такого обращения – 0,05, а для 3-го клиента – 0,02. Определить вероятность того, что в течение года обратится хотя бы 1 клиент, если обращение клиентов – события независимые.

А 2.22. Стрелки А, В и С поражают мишень с вероятностями 0,8, 0,7 и 0,6 соответственно. Был сделан залп по мишени одновременно каждым из стрелков, в результате чего 2 пули попали в цель. Найти вероятность того, что стрелок С: а) попал в цель; б) не попал в цель.

А 2.23. Вероятность того, что проходящая мимо бензоколонки машина подъедет к заправке, равна 0,4. При каком количестве проходящих мимо машин можно сделать вывод, что с вероятностью не меньшей, чем 0,9, можно утверждать, что хотя бы одна из них потребует заправки?

А 2.24. Сколько раз нужно бросить 2 игральные кости, чтобы с вероятностью, не меньшей 0,5, хотя бы один раз появилась сумма очков, равная 12?

А 2.25. Саженец яблони приживается с вероятностью 0,6, груши – 0,5 и винограда – 0,4. Было посажено по 1 дереву каждого вида. Прижилось 2 саженца. Какое событие при этом более вероятно: саженец винограда прижился или саженец винограда не прижился?

А 2.26. Производится подбрасывание игральной кости до появления 6 очков на верхней грани. Найти вероятность того, что придется сделать 5 подбрасываний.

А 2.27. Два стрелка производят стрельбу по мишени, вероятности попадания в которую для каждого стрелка одинаковы и
равны 0,8. Найти вероятность того, что при 3 выстрелах у 1 стрелка будет больше попаданий, чем у 2-го.

А 2.28. На полке имеется 15 тетрадей, из которых 3 в линейку, остальные в клетку. Найти вероятность того, что при случайном изымании 3 тетрадей не более 2 из них будут в клетку.

А 2.29. Вероятность попадания в цель при одном выстреле равна 0,9. Сколько следует произвести выстрелов, чтобы с вероятностью, не меньшей 0,95, был хотя бы один промах?

А 2.30. Вероятность того, что студент ответит на теоретический вопрос билета, равна 0,9, решит предложенную задачу – 0,8.
Какова вероятность того, что студент сдаст экзамен, состоящий из одного теоретического вопроса и двух задач, если для этого необходимо обязательно ответить на теоретический вопрос и решить хотя бы одну задачу?

А 2.31. Вероятность успешной сдачи экзамена по математичес­кой статистике равна 0,7, а при каждой следующей попытке увеличивается на 0,1. Какова вероятность того, что студент не будет отчислен из-за несдачи экзамена по математической статистике, если пересдавать экзамен можно не более 2 раз?

А 2.32. Команда состоит из 2 стрелков, вероятность попадания в цель 1-м из которых равна 0,8; 2-м – 0,9. Каждому разрешено
сделать в случае промаха еще 1 выстрел. Какова вероятность того, что в мишени будет две пробоины?

А 2.33. В продаже имеется 50 альбомов по 50 коп., 30 альбомов – по 70 коп. и 20 альбомов – по 1 грн. Какова вероятность того, что стоимость двух купленных альбомов не превысит 1,5 грн?

А 2.34. Имеется 5 ключей, из которых только один подходит к двери. Ключ подбирается наудачу. Какова вероятность того, что для открывания двери придется сделать не более двух проб?

А 2.35. Изгруппы туристов, отправляющихся за границу, 60% владеют английским языком, 40% – французским и 10% – обоими языками. Найти вероятность того, что наудачу взятый турист будет нуждаться в переводчике.

А 2.36. На рекламной фирме 21% работников получают высокую зарплату. Среди них отношение числа мужчин и женщин равно 14,6:6,4. Известно также, что на фирме работают 40% женщин. Выяснить, существует ли на фирме дискриминация женщин в оплате труда.

А 2.37. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,75, а при наличии конкурирующего товара равна 0,25. Вероятность выпуска конкурентом товара равна 0,35. Найти вероятность того, что товар будет иметь успех.

А 2.38. В течение года две фирмы имеют возможность, независимо друг от друга, обанкротиться с вероятностями 0,06 и 0,09. Найти вероятность того, что в конце года обе фирмы будут функционировать.

А 2.39. На предприятии установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал появляется с вероятностью 0,95. Однако сигнал может возникнуть без аварийной ситуации с вероятностью 0,001. Реальная вероятность аварийной ситуации равна 0,005. Чему равна вероятность аварийной ситуации, если сигнализация сработала?

А 2.40. Из ящика, содержащего 20 стандартных и 10 бракованных изделий, поочередно извлекаются 2 изделия (без возвращения). Какова вероятность при первом и втором извлечениях получить стандартные изделия?

Блок В

В 2.1. На предприятии брак составляет в среднем 2% общего выпуска изделий. Среди годных изделия первого сорта составляют 95%. Какова вероятность того, что наудачу взятое изделие окажется первого сорта, если изделие взято: а) из числа прошедших проверку; б) из общей массы изготовленной продукции?

В 2.2. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что пять первых покупателей потребуют обувь 41-го размера.

В 2.3. Рабочий обслуживает три станка. Вероятность того, что в течение смены потребует его внимания первый станок, равна 0,7, второй - 0,75, третий - 0,8. Найти вероятность того, что в течение смены внимания рабочего потребуют какие-либо два станка.

В 2.4. Среди вырабатываемых рабочим деталей в среднем 4% брака. Какова вероятность того, что среди взятых на испытание пяти деталей не найдется ни одной бракованной?

В 2.5. Для сообщения об аварии установлены два независимо работающие сигнализатора-автомата. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95; второй - 0,9. Найти вероятность того, что при аварии поступит сигнал: а) хотя бы от одного сигнализатора; б) только от одного сигнализатора.

В 2.6. Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность того, что обладатель пяти билетов лотереи выиграет: а) по всем пяти; б) ни по одному; в) хотя бы по одному билету?

В 2.7. В шестиламповом радиоприемнике (все лампы различные) перегорела одна лампа. С целью устранения неисправности наудачу выбранную лампу заменяют исправной из запасного комплекта, после чего сразу проверяют работу приемника. Если приемник заработал – проверку прекращают. Если нет – одну из оставшихся ламп снова заменяют исправной и т.д. Какова вероятность того, что приемник будет нормально работать после замены: а) одной; б) двух; в) трех; г) четырех; д) пяти; е) шести ламп?

В 2.8. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,3, второй - 0,4, третий - 0,7, четвертый - 0,4. Найти вероятность того, что в течение часа ни один станок не потребует внимания рабочего.

В 2.9. Среди 60 электрических лампочек три нестандартные. Найти вероятность того, что две взятые одновременно электролампочки окажутся нестандартными.

В 2.10. В мешке смешаны нити, среди которых 30% белых, а
остальные красные. Определить вероятность того, что вынутые наудачу две нити будут: а) одного цвета; б) разных цветов.

В 2.11. В связке имеются пять различных ключей, из которых только одним можно открыть дверь. Наудачу выбирается ключ и делается попытка открыть им дверь. Ключ, оказавшийся неподходящим, больше не используется. Найти вероятность того, что: а) дверь будет открыта первым ключом; б) для открывания двери будет использовано не более двух ключей.

В 2.12. Радист может трижды вызвать корреспондента. Вероятность того, что будет услышан первый вызов, равна 0,2,
второй - 0,3, третий - 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент услышит вызов радиста.

В 2.13. Два стрелка производят в цель по одному выстрелу. Пусть вероятность попадания для первого стрелка равна 0,7, для второго - 0,8. Найти вероятность того, что попадут в цель: а) оба; б) только один; в) ни один.

В 2.14. Деталь проходит три операции обработки. Вероятность того, что она окажется бракованной после первой операции, равна 0,02, после второй - 0,03, третьей - 0,02. Найти вероятность того, что деталь будет небракованной после трех операций, предполагая, что появление брака на отдельных операциях - независимые события.

В 2.15. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,7, второй - 0,4, третий - 0,4, четвертый - 0,3. Найти вероятность того, что хотя бы один станок в течение часа не потребует внимания рабочего.

В 2.16. Четыре охотника договорились сделать по одному выстрелу по дичи. Следующий охотник производит выстрел лишь в случае промаха предыдущего. Вероятности попадания в цель каждым из охотников одинаковые и равны по 0,8. Найти вероятность того, что будет произведено: а) один, б) два, в) три, г) четыре выстрела.

В 2.17. Экзаменационный билет содержит три вопроса. Вероятности того, что студент ответит на первый, второй вопросы, равны по 0,9, на третий - 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить: а) на все вопросы; б) по крайней мере на два вопроса билета.

В 2.18. Брак в продукции завода вследствие дефекта А составляет 5%, причем среди забракованной по признаку А продукции в 10% случаев встречается дефект В, а в продукции, свободной от дефекта А, дефект В встречается в 1% случаев. Найти вероятность того, что дефект В не встретится во всей продукции.

В 2.19. Брак в продукции завода вследствие дефекта А составляет 4%, а вследствие дефекта В - 3,5%. Годная продукция завода составляет 95%. Найти вероятность того, что: а) среди продукции, не обладающей дефектом А, встретится дефект В; б) среди забракованной по признаку А продукции встретится дефект В.

В 2.20. Пусть вероятность попадания в движущуюся цель при одном выстреле постоянна и равна 0,05. Сколько необходимо сделать выстрелов для того, чтобы с вероятностью, не меньшей 0,75, иметь хотя бы одно попадание?

В 2.21. Заводом послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0,9, на второй - 0,95, на третьей - 0,8, на четвертой - 0,6. Найти вероятность того, что только на одной базе не окажется нужного материала.

Блок С

С 2а Вероятность попадания в цель первым охотником равна 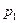, вторым – 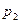. Найти вероятность того, что:

а) оба попадут; б) ни один не попадет;

в) хотя бы один попадет; г) только один попадет в цель?

Номер варианта	Исходные данные	Номер варианта	Исходные данные
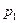
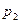
С 2.1	0,7	0,6	С 2.6	0,55	0,6
С 2.2	0,7	0,8	С 2.7	0,65	0,8
С 2.3	0,75	0,55	С 2.8	0,7	0,9
С 2.4	0,65	0,8	С 2.9	0,75	0,8
С 2.5	0,9	0,75	С 2.10	0,9	0,65

С 2б Диспетчер обслуживает три линии. Вероятность того, что на протяжении часа обратятся по первой линии, составляет 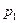, по второй – 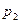, по третьей – 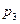. Какая вероятность того, что на протяжении часа диспетчер получит вызовы:

а) с одной линии;

б) хотя бы с одной линии;

в) не меньше чем с двух линий?

Номер варианта	Исходные данные	Номер варианта	Исходные данные
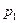
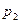
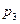
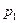
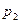
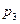
С 2.11	0,2	0,4	0,3	С 2.16	0,3	0,25	0,18
С 2.12	0,3	0,15	0,2	С 2.17	0,5	0,1	0,15
С 2.13	0,2	0,18	0,16	С 2.18	0,1	0,25	0,18
С 2.14	0,4	0,35	0,18	С 2.19	0,2	0,15	0,3
С 2.15	0,1	0,2	0,25	С 2.20	0,3	0,18	0,35

С 2в Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 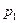, на второй – 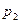, на третий – 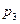. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить:

а) на все вопросы;

б) хотя бы на два вопроса билета?

Номер варианта	Исходные данные	Номер варианта	Исходные данные
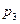
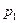
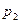
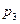
С 2.21	0,7	0,6	0,8	С 2.26	0,6	0,85	0,9
С 2.22	0,8	0,65	0,9	С 2.27	0,7	0,9	0,85
С 2.23	0,6	0,75	0,7	С 2.28	0,8	0,58	0,9
С 2.24	0,7	0,85	0,9	С 2.29	0,6	0,78	0,85
С 2.25	0,8	0,9	0,65	С 2.30	0,5	0,9	0,8

Дата добавления: 2014-11-18