Решение типовых задач. Теоремы сложения и умножения вероятностей

Теоремы сложения и умножения вероятностей

Тема 2

Для использования теоремы сложения вероятностей важно установить несовместность событий. Если события-слагаемые совместны, то для нахождения вероятности их суммы иногда целесообразно перейти к противоположному событию.

Теорема умножения требует предварительного анализа независимости или зависимости событий-сомножителей. В последнем случае для применения этой теоремы используются условные вероятности.

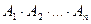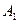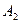Запись события С в виде суммы С = или произведения С = событий становится более понятной, если пользоваться логическим определением этих алгебраических операций над событиями: событие означает наступление или , или , или..., или 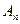; событие 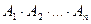означает наступление 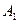и , и 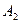, и..., и 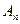(одновременно).

Задача 1. Вероятность сдать каждый из 3 экзаменов сессии на отлично для студента М равна соответственно 0,8, 0,7 и 0,75. Найти вероятность того, что студент сдаст на отлично: а) все три экзамена; б) два экзамена; в) хотя бы один.

Решение. Обозначим события:

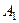– студент сдаст 1-й экзамен на отлично;

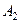– студент сдаст 2-й экзамен на отлично;

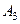– студент сдаст 3-й экзамен на отлично.

Противоположные им события 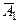, , 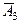соответственно. По условию вероятности этих событий равны:

; ; ;

; ; .

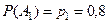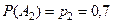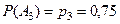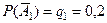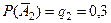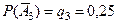а) Обозначим через А событие, состоящее в том, что студент сдаст на отлично все 3 экзамена, т.е. и первый (событие 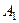), и второй (событие 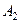), и третий (событие 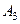). Тогда .

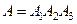Вероятность события А найдем по теореме умножения для независимых событий:

.

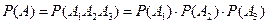
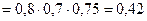б) Обозначим через В событие, состоящее в том, что студент сдаст два из трех экзаменов на отлично. Событие В через события 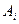и 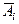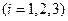можно представить следующим образом: .

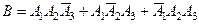Применяя теорему сложения для несовместных событий, а затем теорему умножения для независимых событий, находим вероятность события В:

.

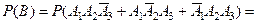
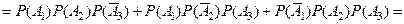
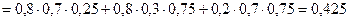в) Обозначим через С событие, состоящее в том, что хотя бы один экзамен из трех студент сдаст на отлично. Тогда противоположное ему событие 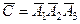– ни один экзамен студент не сдаст на отлично.

По следствию из теоремы сложения вероятностей получим

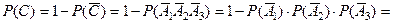
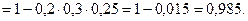
Задача 2. В ящике 50 кубиков, из которых 5 неокрашенных. Наудачу последовательно извлекаются 3 кубика. Определить вероятность того, что все извлеченные кубики окрашены.

Решение. Обозначим события:

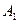– 1-й извлеченный кубик окрашен;

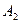– 2-й извлеченный кубик окрашен;

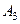– 3-й извлеченный кубик окрашен.

Эти события зависимые, их вероятности находим по формулам:

, , .

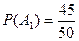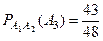Обозначим через D событие, состоящее в том, что все 3 кубика окрашены. Это событие можно представить в виде 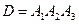, тогда его вероятность найдем по теореме умножения вероятностей для зависимых событий:

.

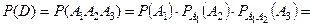
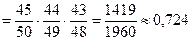Дата добавления: 2014-11-18