Основные теоретические сведения. Оценка показателей надёжности по результатам наблюдений для нормального закона распределения

Оценка показателей надёжности по результатам наблюдений для нормального закона распределения

Практическая работа № 7

Ц е л ь р а б о т ы: определить точечные оценки показателей надежности по параметрам наиболее распространенного закона распре­деления (нормального, Гаусса) методом максимального правдоподобия в зависимости от плана наблюдений в условиях эксплуатации.

Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор; таблица исходных данных.

Нормальное распределение является основным в математической статистике. Оно образуется, когда на случайную величину действует большое число равноправных факторов.

В теории надежности нормальным распределением описывают нара­ботки на отказ элементов вследствие их износа и старения.

Под оценками показателей надежности понимают числовые значения показателей, определяемые по результатам наблюдений за изделиями в условиях эксплуатации. За числовое значение показателя принимают точечную оценку или доверительные границы интервала, который с за­данной доверительной вероятностью покрывает истинное значение по­казателя. Точечную оценку принимают за приближенное значение не­известного показателя.

Определение точечной оценки параметров нормального закона распределения

Функция плотности вероятности задана в следующем виде:

, при t≥0

точечную оценку параметров a и σ вычисляют соответственно по формулам (85), (86) для плана наблюдений [N,U,T]:

оценка параметра a:

, (85)

оценка параметра σ:

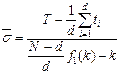, (86)

где N - число изделий, поставленных под наблюдение; d - число отказов за время наблюдения Т; t_i - отдельные значения случайной величины (наработки каждого изделия до отказа); k - коэффициент, рассчитанный по формуле (для плана [ N,U,T ]):

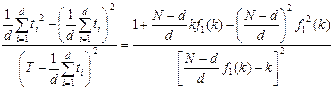(87)

где значение f₁(k) определяют по табл. 23.

Точечные сценки показателей надежности рассчитывают по формулам по точечным опенкам параметров закона распределения в зависимости от закона распределения случайной величины: наработки до отказа, ресурса, срока службы, срока сохраняемости, времени восстановления.

Таблица 23

Значения f₁(k), f₂(k), f₃(k)

k	f1(k)	f2(k)	f3(k)
-2,0	2,373	1,003	0,519
-1,9	2,285	1,004
-1,3	2,197	1,005	0,530
-1,7	2,110	1,006	0,537
-1,6	2,024	1,009	0,546
-1,5	1,939	1,011	0,556
-1,4	1,854	1,015	0,568
-1,3	1,770	1,019	0,583
-1,2	1,688	1,025	0,600
-1,1	1,606	1,032	0,620
-1,0	1,525	1,042	0,643
-0,9	1,446	1,054	0,671
-0,8	1,376	1,069	0,702
-0,7	1,290	1,089	0,740
-0,6	1,215	1,114	0,783
-0,5	1,141	1,147	0,833
-0,4	1,069	1,189	0,891
-0,3	0,998	1,243	0,959
-0,2	0,929	1,312	1,039
-0,1	0,868	1,401	1,132
	0,790	1,517	1,214
0,1	0,735	1,667	1,370
0,2	0,675	1,863	1,523
0,3	0,671	2,119	1,704
0,4	0,562	2,458	1,919
0,5	0,509	2,893	2,178
0,7	0,459	3,473	2,488
0,9	0,412	4,241	2,863
Окончание табл. 23
1,1	0,368	5,261	3,319
1,3	0,326	6,623	3,876
1,6	0,288	8,448	4,561
1,7	0,252	10,90	5,408
1,9	0,190	14,220	6,462
0,6	0,163	18,730	7,780
0,8	0,139	24,890	9,442
1,0	0,117	33,340	11,550
1,2	0,098	44,990	14,240
1,4	0,082	61,130	17,240
1,6	0,068	83,640	22,190
1,8	0,068	115,200	28,050
2,0	0,055	159,700	35,740

Для нормального закона распределения это формулы:

средняя наработка до первого отказа: Т_ср= ,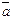

средний ресурс: Т_р.с. = ,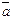

средний срок службы: Т_сл.ср = ,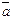

средний срок сохраняемости: Т_с.ср= ,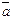

среднее время восстановления: Т_В.ср. = ,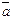

гамма – процентный срок службы:

, (88)

гамма – процентный срок сохраняемости:

, (89)

гамма – процентный ресурс:

, (90)

вероятность безотказной работы до первого отказа:

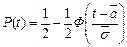, (91)

вероятность восстановления:

, (92)

интенсивность отказов:

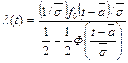(93)

интенсивность восстановления:

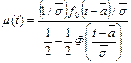(94)

t_γ - обозначает гамма-процентный ресурс, гамма-процентный срок службы или гамма-процентный срок сохраняемости.

Как видно, один и тот же параметр закона распределения обозначает различия величины, в зависимости от того, в выражение какого показа­теля надежности он входит.

Определение доверительных границ для параметров нормального закона распределения

Точечные оценки параметров законов распределения являются случайными величинами и должны оцениваться на достоверность доверительными границами с заданной доверительной вероятностью.

Доверительные границы для параметров нормального закона распределения

По табл. 24 … 28 определяют двусторонние и односторонние доверительные границы для параметров a и σ с вероятностью β.

Вероятность P с учетом формул табл. 25, 26 принимают следующий вид:

β; 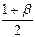; n=N-1.

Таблица 24

Дата добавления: 2014-11-18