Основные теоретические сведения. Обработка эмпирических данных, принадлежащих экспоненциальному закону распределения

Обработка эмпирических данных, принадлежащих экспоненциальному закону распределения

Практическая работа № 5

Результаты расчета параметров очередных замен

Расчет вероятностей безотказной работы

Показатели

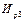
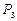
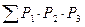
Таблица 14

Показатели
t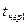

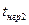
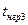
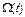
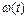
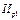
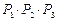
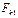
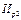
Ц е л ь р а б о т ы: изучить методы обработки эмпирических данных по результатам подконтрольной эксплуатации технологических систем при экспоненциальном распределении с проверкой гипотезы о виде закона распределения критерием согласия W. Вычислить показатели надежности и их доверительные границы.

Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор

Непрерывная случайная положительная величина Т называется распределенной по экспоненциальному закону, если ее плотность вероятности может быть определена соотношением:

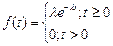, (50)

где параметр закона распределения. Этот параметр связан с математическим ожиданием а равенством:

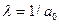. (51)

Для экспоненциального распределения математическое ожидание равно среднему квадратичному отклонению, т.е. .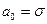

При исследовании надежности технических систем может выражать интенсивность отказов или интенсивность восстановления, а величина среднюю наработку до первого отказа, средний ресурс, средний срок службы, средний срок сохраняемости, среднее время восстановления.

Вероятность безотказной работы до первого отказа на интервале от 0 до t вычисляется по формуле:

. (52)

При известной характеристике параметр определяется:

. (53)

Вероятность восстановления определяется по формуле:

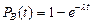. (54)

Связь основных характеристик для любого закона распределения выражается соотношением:

. (55)

Гамма-процентный срок службы, гамма-процентный ресурс и гамма-процентный срок сохраняемости определяется по формуле:

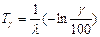. (56)

При проверке согласия эмпирических распределений для экспоненциального закона, когда число наблюдений n=7…35 может эффективно использоваться критерием 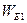предложенный Шапиро и Унаком:

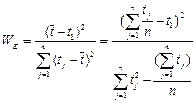. (57)

Экспоненциальное распределения имеет большое практическое значение. Оно применяется для описания отказов агрегатов и технологических систем, работающих в тяжелых условиях под воздействием химических и температурных нагрузок, а также при анализе внезапных отказов, когда явления износа и старения выражены весьма слабо и ими можно пренебречь.

Этому распределению могут подчиняться: случайная наработка до отказа или между отказами; случайная длительность проверки или контроля агрегатов и технологических систем; случайная длительность некоторой операции; случайная длительность технического обслуживания технологических систем.

Дата добавления: 2014-11-18