Основные теоретические сведения. Определение оценок и доверительных границ для параметров логарифмически нормального распределения

Определение оценок и доверительных границ для параметров логарифмически нормального распределения

Практическая работа № 6

Результаты расчета

n

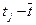
Ц е л ь р а б о т ы: найти оценки параметров и для логарифмически нормального определения.

Н е о б х о д и м о е о б о р у д о в а н и е: микрокалькулятор; таблица исходных данных.

Логарифмически нормальное распределение весьма часто встречается на практике. Оно возникает в задачах надежности технических систем (например, срок службы некоторых типов изделий, в экономических исследованиях и др.). Ему, как правило, подчиняются размеры частиц при дроблении, и поэтому оно встречается в геологии (процентное содержание минералов в природе) и др.

В данной работе уже известно, что распределение изучаемой случайной величины логарифмически нормально, и требуется оценить его параметры.

Следует иметь в виду, что, на не слишком больших отрезках функции логарифмически нормального распределения мало отличается от функции нормального распределения. Поэтому рекомендуется следующее правило: если распределение логарифмически нормально, но выборочный коэффициент вариации, т.е. отношение выборочной дисперсии к выборочному среднему, меньше 0,3, то можно считать, что исследуемая величина распределена нормально, и обрабатывать данные соответствующим образом.

Распределение положительной случайной величины Х называется логарифмически нормальным, если случайная величина

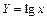(72)

имеет нормальное распределение (см. ГОСТ 11.004-74).

Функция распределения величины Х имеет вид:

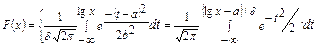при Х>0 (73)

0 при Х 0

Таким образом, и являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Y, определенной по формуле (72).

Плотность распределения величины Х имеет вид

при X>0 (74)

0 при Х 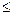0

где .

Оценку параметра находят по формуле

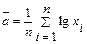(75)

где - совокупность наблюдений значений случайной величины Х; n -число изделий, поставленных на испытание, или число испытаний.

Если значения параметра неизвестно, то оценка S² параметра

, (76)

где 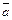определяют по формуле (94)

Оценка 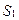параметра

(77)

где 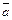вычисляют по формуле (94).

Оценку 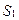можно использовать в тех случаях, когда не требуется большая точность вычислений. Поэтому надо найти также несмещенную оценку для :

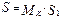, (78)

где М_к определяют по табл. 17 при K=n-1.

Определение доверительных границ для параметра а

Нижнюю и верхнюю доверительные границы (соответственно а_н и а_В для параметра а при известном значении параметра σ находят по следующим формулам:

(79)

(80)

где - вычисляют по формуле (75), а u_γ - по таблицам.

Таблица 17

Значения коэффициентов М_K

К	МK	K	МK	К	МK
	1,253		1,025		1,013
	1,128		1,023		1,013
	1,085		1,021		1,010
	1,064		1,019		1,008
	1,051		1,018		1,007
	1,042		1,017		1,006
	1,036		1,016		1,006
	1,032		1,015		1,005
	1,028		1,014		1,004

Доверительные границы для параметра a при неизвестном значении σ находят по формулам:

(81)

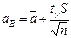(82)

где и S определяют соответственно по формулам (75) и (78), а t_γ - в табл. 18 по заданным значениям n - 1 и γ.

Определение доверительных границ для параметра σ

Нижнюю и верхнюю доверительные границы для параметра σ (соот­ветственно σ_Н и σ_В) определяют по следующим формулам:

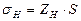(83)

(84)

где S находят по формуле (78), Z_Н и Z_В – соответственно по табл. 19 и 20 при К=n-1, если значения параметра а неизвестны.

Таблица 18

Значения коэффициентов t_γ

n -1	Значения коэффициентов tγ при односторонней доверительной вероятности γ
0,80	0,90	10,95	0,975	0,990	0,995	0,9975	0,9990
	1,375	3,078	6,314	12,71	31,82	63,66	127,3	318,3
	1,061	1,886	2,920	4,303	6,965	9,925	14,09	22,33
	0,978	1,638	2,353	3,182	4,541	5,841	7,453	10,21
	0,941	1,533	2,132	2,776	3,747	4,604	5,598	7,173
	0,920	1,476	2,015	2,571	3,365	4,032	4,773	5,893
	0,906	1,440	1,943	4,447	3,143	3,707	4,317	5,208
	0,896	1,415	1,895	2,365	2,998	3,449	4,029	4,785
	0,889	1,397	1,859	2,306	2,896	3,335	3,832	4,501
	0,883	1,383	1,833	2,252	2,821	3,250	3,690	4,297
	0,879	1,372	1,812	2,228	2,764	3,169	3,581	4,144
	0,876	1,363	1,796	2,201	2,713	3,106	3,497	4,025
	0,873	1,356	1,782	2,170	2,680	3,054	3,497	3,930
	0,870	1,350	1,771	2,160	2,650	3,012	3,373	3,852
	0,868	1,345	1,761	2,145	2,624	2,977	3,326	3,787
	0,866	1,341	1,753	2,131	2,602	2,947	3,286	3,286
	0,865	1,337	1,746	2,120	2,583	2,921	3,252	3,686
	0,863	1,333	1,740	2,110	2,567	2,898	3,222	3,646
	0,862	1,330	1,734	2,101	2,552	2,878	3,197	3,611
	0,861	1,328	1,729	2,093	2,539	2,861	3,174	3,579
	0,860	1,325	1,725	2,086	2,528	2,845	3,153	3,552
	0,859	1,323	1,721	2,080	2,518	2,831	3,135	3,527
	0,858	1,321	1,717	2,074	2,508	2,819	3,119	3,505
	0,858	1,319	1,714	2,069	2,500	2,807	3,104	3,485
Окончание табл.18
	0,857	1,318	1,711	2,064	2,492	2,797	3,090	3,467
	0,856	1,316	1,708	2,060	2,485	2,787	3,078	3,450
	0,856	1,315	1,706	2,056	2,479	2,779	3,067	3,435
	0,855	1,314	1,703	2,052	2,473	2,771	3,056	3,421
	0,855	1,313	1,701	2,048	2,467	2,763	3,047	3,408
	0,854	1,311	1,699	2,045	2,462	2,756	3,038	3,396
	0,854	1,310	1,697	2,042	2,457	2,750	3,030	3,385
	0,853	1,309	1,694	2,037	2,449	2,737	3,015	3,365
	0,853	1,307	1,691	2,032	2,441	2,728	3,002	3,348
	0,852	1,305	1,688	2,028	2,434	2,719	2,990	3,333
	0,852	1,304	1,686	2,024	2,429	2,712	2,980	3,319
	0,851	1,303	1,684	2,021	2,423	2,704	2,971	3,307

Таблица 19

Значения коэффициентов Z_Н

К	Значения коэффициентов ZН при односторонней доверительной вероятности γ
0,80	0,90	0,95	0,975	0,990	0,995	0,9975	0,9990
	0,788	0,788	0,578	0,521	0,466	0,434	0,408	0,380
	0,804	0,804	0,620	0,566	0,514	0,483	0,457	0,429
	0,817	0,817	0,649	0,599	0,549	0,519	0,493	0,455
	0,828	0,828	0,672	0,624	0,576	0,546	0,521	0,494
	0,837	0,837	0,690	0,644	0,597	0,569	0,544	0,517
	0,845	0,845	0,705	0,661	0,616	0,588	0,563	0,536
	0,852	0,852	0,718	0,675	0,631	0,604	0,580	0,553
	0,859	0,788	0,729	0,688	0,645	0,618	0,549	0,568
	0,864	0,804	0,699	0,739	0,656	0,630	0,607	0,581
Окончание табл.19
	0,869	0,817	0,748	0,708	0,667	0,641	0,619	0,593
	0,872	0,828	0,755	0,717	0,677	0,651	0,629	0,604
	0,874	0,837	0,762	0,725	0,685	0,660	0,638	0,614
	0,877	0,845	0,769	0,732	0,693	0,669	0,647	0,623
	0,881	0,852	0,775	0,739	0,700	0,676	0,655	0,631
	0,884	0,859	0,780	0,745	0,707	0,683	0,662	0,638
	0,886	0,864	0,785	0,713	0,690	0,690	0,669	0,646
	0,888	0,869	0,790	0,756	0,719	0,696	0,675	0,652
	0,836	0,872	0,760	0,725	0,725	0,702	0,681	0,658
	0,894	0,874	0,798	0,765	0,730	0,687	0,707	0,664
	0,898	0,877	0,773	0,739	0,739	0,717	0,697	0,675
	0,901	0,881	0,812	0,781	0,747	0,726	0,707	0,685
	0,904	0,884	0,818	0,788	0,755	0,734	0,715	0,694
	0,907	0,886	0,823	0,794	0,762	0,741	0,723	0,702
	0,909	0,888	0,828	0,799	0,768	0,748	0,730	0,709
	0,915	0,836	0,838	0,811	0,781	0,762	0,745	0,725
	0,919	0,894	0,847	0,821	0,792	0,774	0,757	0,738
	0,923	0,898	0,854	0,829	0,802	0,784	0,768	0,750
	0,927	0,901	0,861	0,837	0,810	0,793	0,777	0,760
	0,932	0,904	0,871	0,349	0,824	0,808	0,793	0,776
	0,937	0,907	0,879	0,858	0,835	0,820	0,805	0,789
	0,941	0,909	0,88§	0,866	0,844	0,829	0,815	0,801
	0,943	0,915	0,892	0,373	0,852	0,338	0,825	0,810
	0,946	0,919	0,897	0,879	0,858	0,845	0,832	0,818

Таблица 20

Значения коэффициентов Z_В

К	Значения коэффициентов ZВ при односторонней доверительной вероятности γ
0,80	0,90	0,95	0,975	0,990	0,995	0,9975	0,9990
	2,12	3,08	4,42	6,28	9,97	14,1	19,89	31,6
	1,73	2,27	2,92	3,73	5,11	6,47	8,19	11,1
	1,56	1,94	2,37	2,87	3,67	4,40	5,29	6,64
	1,46	1,76	2,09	2,45	3,00	3,48	4,04	4,88
	1,40	1,65	1,92	2,20	2,62	2,98	3,38	2,97
	1,35	1,57	1,80	2,04	2,38	2,66	2,97	3,42
	1,32	1,51	1,71	1,92	2,20	2,44	2,69	3,06
	1,29	1,47	1,65	1,83	2,08	2,28	2,49	2,79
	1,27	1,43	1,59	1,75	1,98	2,15	2,34	2,60
	1,25	1,40	1,55	1,70	1,90	2,06	2,22	2,45
	1,24	1,38	1,52	1,65	1,83	1,98	2,13	2,33
	1,23	1,36	1,49	1,61	1,78	1,91	2,05	2,23
	1,22	1,34	1,46	1,58	1,73	1,85	1,98	2,15
	1,21	1,32	1,44	1,55	1,69	1,81	1,93	2,08
	1,20	1,31	1,42	1,52	1,66	1,76	1,87	2,01
	1,19	1,30	1,40	1,50	1,63	1,73	1,83	1,96
	1,18	1,28	1,38	1,48	1,60	1,70	1,79	1,92
	1,18	1,27	1,37	1,46	1,58	1,67	1,75	1,87
	1,17	1,26	1,36	1,44	1,56	1,64	1,72	1,84
	1,16	1,25	1,34	1,42	1,52	1,60	1,67	1,77
	1,15	1,24	1,32	1,39	1,49	1,56	1,63	1,72
	1,15	1,23	1,30	1,37	1,46	1,53	1,59	1,72
Окончание табл.20
	1,14	1,22	1,29	1,35	1,44	1,50	1,56	1,64
	1,13	1,21	1,27	1,34	1,42	1,48	1,53	1,61
	1,12	1,19	1,25	1,30	1,38	1,43	1,47	1,54
	1,11	1,17	1,23	1,28	1,34	1,39	1,43	1,49
	1,10	1,16	1,21	1,26	1,32	1,36	1,40	1,46
	1,10	1,15	1,20	1,24	1,30	1,34	1,37	1,42
	1,09	1,14	1,18	1,22	1,27	1,30	1,33	1,37
	1,08	1,13	1,16	1,20	1,24	1,27	1,30	1,34
	1,08	1,12	1,15	1,18	1,22	1,25	1,27	1,31
	1,07	1,11	1,14	1,17	1,21	1,23	1,25	1,29
	1,07	1,10	1,13	1,16	1,19	1,22	1,24	1,27

Доверительный интервал (бесконечный в одностороннем случае и ко­нечный в двустороннем) накрывает значение параметра с вероятностью γ в одностороннем случае и γ* в двустороннем.

Дата добавления: 2014-11-18