Теоремы о пределах последовательностей

Теорема 1. .

Теорема 2 (арифметические операции с пределами). Пусть последователь- ност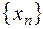и и 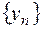- сходящиеся. Тогда сходящимися будут и такие последовательности: 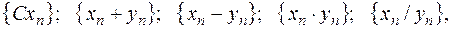если только . При этом:

1)

2)

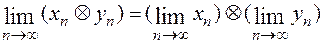
(здесь - символ любой арифметической операции).

Ограничимся доказательством сходимости частного. Пусть , где и . Преобразуем частное следующим образом:

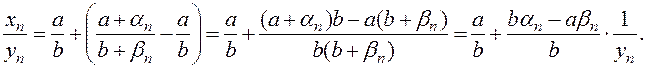В полученном выражении 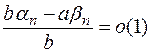, как линейная комбинация бесконечно малых, а 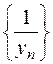- ограничена, т.к. 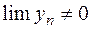. Следовательно,

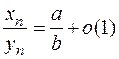. Это и доказывает: .

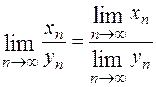Теорема 3 (предельный переход в неравенствах). Пусть последовательност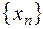и и 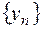- сходящиеся. Тогда, если (или 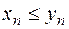), то и . В частности:

а) если , то ;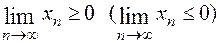

б) если 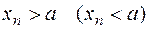, то .

Теорема 4 (достаточное условие сходимости). Если 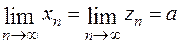и для всех 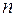справедливо неравенств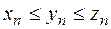о , то .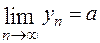

Для доказательства воспользуемся определением предела на языке окрестностей. Рассмотрим произвольную -окрестность числа . Обозначим ее . Так как 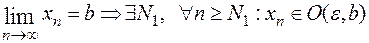, а так как . Тогда в силу неравенства 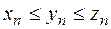имеем: . Итак, для произвольной -окрестности мы нашли номер , начиная с которого члены 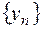принадлежат этой окрестности. Это и означает, что .

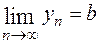Пример. Рассмотрим последовательность с общим членом .

Чтобы оценить сверху, заменим каждое слагаемое наибольшим (это первое слагаемое), а чтобы оценить снизу, заменим слагаемые наименьшим (это последнее). Получим

или .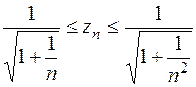

Подкоренные выражения обеих корней имеют вид 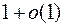, следовательно, сходятся к 1. Значит, .

Отсюда вытекает, что .

Замечание 1. При решении примера было использовано одно свойство элементарных функций, вытекающее из их непрерывности: если члены 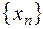и её принадлежат области определения элементарной функции , то знак предела можно вносить под знак функции

.

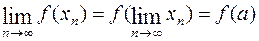Замечание 2. Обратим внимание на следующее. Общий член представляет собой сумму 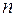слагаемых, каждое из которых является бесконечно малой. Однако, здесь нельзя сказать, что сумма б.м. есть б.м., ибо число слагаемых неограниченно возрастает.

§8. Монотонные последовательности. Число

I О пределе монотонной последовательности

Уже известно, что сходящаяся последовательность – ограничена. Однако, не всякая ограниченная последовательность имеет конечный предел: примером может служить последовательность .

Одним из условий, обеспечивающих существование предела, является монотонность ограниченной последовательности.

Теорема. 1. Всякая ограниченная монотонная последовательность имеет конечный предел. 2. Всякая неограниченная монотонная последовательность является бесконечно большой (определенного знака).

Заметим, что для убывающей последовательности достаточно доказывать ограниченность снизу, а для возрастающей – ограниченность сверху.

Пример. Рассмотрим последовательность с общим членом 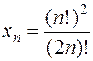. Для доказательства монотонности преобразуем член :

.

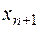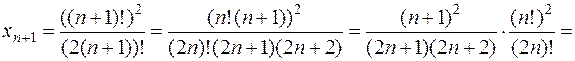
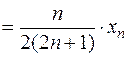Мы получили рекуррентное соотношение

, где .

Члены данной последовательности положительны, а 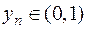, следовательно, 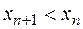, т.е. 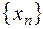- убывает. Ее ограниченность снизу очевидна, ибо .

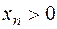Сформулированная выше теорема обеспечивает существование конечного предела . Для последовательности 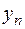нетрудно получить:

, т.е. .

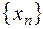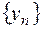Теперь перейдем к пределу в обеих частях рекуррентного соотношения, причем в правой части имеем право использовать теорему о пределе произведения (ибо и - сходящиеся):

или .

Отсюда получаем: .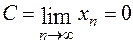

II Число е

Рассмотрим последовательность с общим членом

и попытаемся применить к ней теорему, сформулированную выше.

Монотонный характер 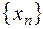непосредственно не усматривается, так как с возрастанием показателя степени 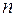основание степени убывает. Чтобы убедиться в монотонности, разложим степень по формуле бинома Ньютона:

.

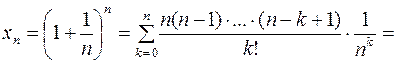
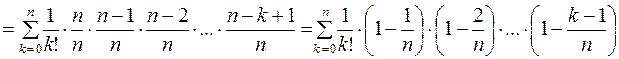Если теперь от 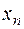перейти к 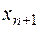, т.е. увеличить 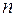на единицу, то, во-первых, добавится еще одно (положительное) слагаемое, а, во-вторых, каждое из уже написанных слагаемых увеличится, ибо множители вида заменятся большими множителями . Отсюда следует, что ,

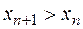т.е. последовательность 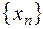- возрастающая.

В последнем выражении для 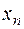опустим все скобки. Тем самым каждое слагаемое увеличится и мы получим оценку: .

Учитывая, что , усилим эту оценку:

.

(Здесь использована формула для суммы геометрической прогрессии). Итак, последовательность 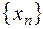возрастает и ограничена сверху, следовательно, она имеет конечный предел. Его обозначают буквой . Это число

имеет исключительную важность, как для самого математического анализа, так и для его приложений.

Лекция 5

Дата добавления: 2014-11-08