
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции
|
|
|
|
I Общее определение
Договоримся о терминологии. Термин «число  » означает как обычное число, так и один из символов:
» означает как обычное число, так и один из символов: 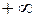 или
или 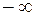 . Термин «точка
. Термин «точка 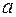 » означает как конченую точку, так и «бесконечно удаленную»:
» означает как конченую точку, так и «бесконечно удаленную»: 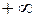 ,
, 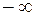 или
или 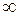 . При этом под окрестностью такой «бесконечно удаленной» точки понимается интервал
. При этом под окрестностью такой «бесконечно удаленной» точки понимается интервал 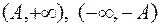 или объединение этих интервалов соответственно (при произвольном
или объединение этих интервалов соответственно (при произвольном 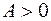 ).
).
Окрестностью же конечной точки понимаем любой интервал, содержащий эту точку. Для простоты формулировок и для бесконечно больших последовательностей будем говорить: «последовательность сходится (к 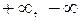 или
или 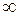 )».
)».
Рассмотрим функцию 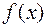 , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки 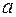 (за исключением, быть может, самой точки
(за исключением, быть может, самой точки 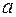 ) и возьмем из этой окрестности последовательность точек
) и возьмем из этой окрестности последовательность точек

отличных от 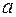 и сходящуюся к
и сходящуюся к 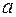 . Значения функции в точках этой последовательности также образуют числовую последовательность
. Значения функции в точках этой последовательности также образуют числовую последовательность
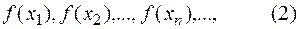
и можно ставить вопрос существования ее предела.
Определение 1 (язык последовательностей). Число  называют пределом функции
называют пределом функции 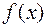 в точке
в точке 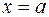 (или при
(или при  ) и пишут
) и пишут
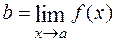 (или:
(или: 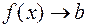 при
при  ),
),
если для любой сходящейся к 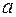 последовательности (1) значений аргумента
последовательности (1) значений аргумента  , отличных от
, отличных от 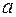 , соответствующая последовательность (2) значений функции сходится к числу
, соответствующая последовательность (2) значений функции сходится к числу  .
.
Геометрический смысл равенства 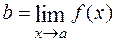 : график функции в окрестности точки
: график функции в окрестности точки 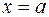 приближается (стремится) к точке
приближается (стремится) к точке 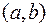 .
.
Пример 1. Вычислим предел 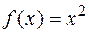 в точке
в точке 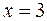 . Рассмотрим произвольную последовательность
. Рассмотрим произвольную последовательность 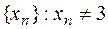 и
и 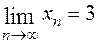 . Для соответствующей последовательности значений функции
. Для соответствующей последовательности значений функции 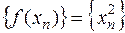 имеем
имеем 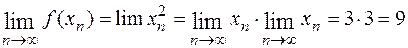 . Таким образом,
. Таким образом, 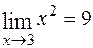 .
.
Пример 2. Покажем, что предел функции 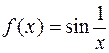 при
при 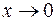 не существует. Рассмотрим две последовательности значений аргумента с членами
не существует. Рассмотрим две последовательности значений аргумента с членами 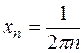 и
и 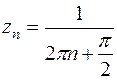 . Очевидно, что
. Очевидно, что 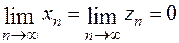 . При этом для последовательностей значений функции:
. При этом для последовательностей значений функции:
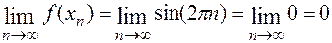 ,
,
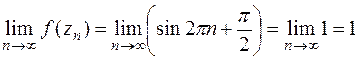 .
.
Таким образом, для двух сходящихся к 0 последовательностей значений аргумента соответствующие последовательности значений функций имеют разные пределы. А это по определению предела функции и означает, что 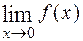 не существует.
не существует.
II Частные случаи. Важные понятия
А) Предел на бесконечности (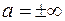 ).
).
Определение 2.
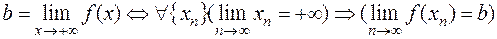 .
.
Аналогичное определение и для 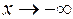 .
.
Пример 3. 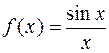 ,
, 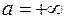 . Рассмотрим
. Рассмотрим 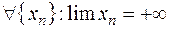 . Тогда для последовательности значений функции
. Тогда для последовательности значений функции 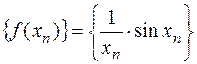 будем иметь:
будем иметь: 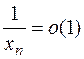 , т.к.
, т.к. 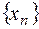 - б.б., а
- б.б., а 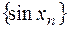 - ограничена, значит
- ограничена, значит 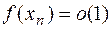 , т.е.
, т.е. 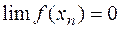 . Это означает, что
. Это означает, что 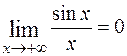 .
.
Нетрудно убедиться, что и 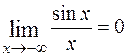 . Для тех функций, для которых
. Для тех функций, для которых 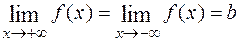 , можно писать
, можно писать 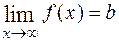 . Напротив, писать
. Напротив, писать 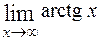 нельзя, ибо
нельзя, ибо 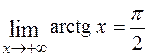 , а
, а 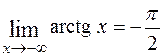 .
.
Геометрическая иллюстрация: конечный предел функции на 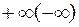 означает наличие у графика функции горизонтальной асимптоты на
означает наличие у графика функции горизонтальной асимптоты на 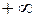 (на
(на 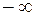 ).
).
В) Бесконечно малые функции (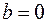 ).
).
Определение 3. Функцию 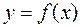 называют бесконечно малой (б.м.) в точке
называют бесконечно малой (б.м.) в точке 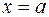 (или: при
(или: при  ) и пишут «
) и пишут «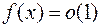 при
при  », если
», если 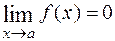 , т.е.
, т.е.
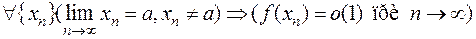 .
.
Например, в предыдущем пункте мы показали, что 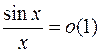 при
при 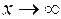 .
.
Основной результат дает следующая теорема.
Теорема 1. Функция 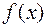 имеет в точке
имеет в точке 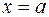 предел
предел 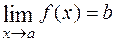 тогда и только тогда, когда разность
тогда и только тогда, когда разность 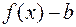 есть б.м. при
есть б.м. при  :
:
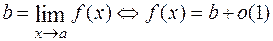 при
при  .
.
С) Бесконечно большие функции (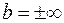 ).
).
Определение 4. Функцию 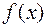 называют бесконечно большой (б.б.) в точке
называют бесконечно большой (б.б.) в точке 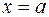 (при
(при  ), если
), если 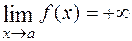 или
или 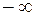 , т.е.
, т.е.
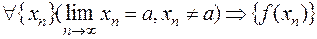 - б.б. последовательность опреде-ленного знака.
- б.б. последовательность опреде-ленного знака.
Все свойства б.м. и б.б. последовательностей остаются справедливыми и для б.м. и б.б. функций. Приведем лишь некоторые из них.
Теорема 2. Для того, чтобы функция 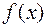 была бесконечно большой в точке
была бесконечно большой в точке 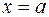 необходимо и достаточно, чтобы функция
необходимо и достаточно, чтобы функция 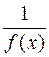 была бесконечно малой в этой же точке.
была бесконечно малой в этой же точке.
И два свойства.
1) Если 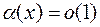 при
при  , а
, а 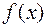 - ограничена в некоторой окрестности точки
- ограничена в некоторой окрестности точки 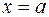 , то произведение
, то произведение 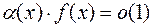 при
при  .
.
2) Если 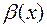 - б.б. в точке
- б.б. в точке 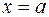 , а
, а 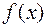 такова, что
такова, что  , то произведение
, то произведение 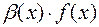 есть б.б. функция при
есть б.б. функция при  .
.
Например, 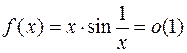 в точке
в точке 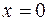 , а многочлен
, а многочлен 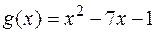 есть б.б. на
есть б.б. на 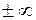 , ибо
, ибо 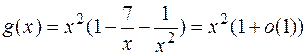 .
.
Эталонные б.б. и б.м. функции приведем в таблице.
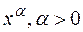
| 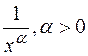
| 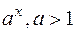
| 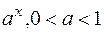
| 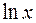
| |
| б.м | 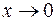
| 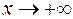
| 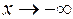
| 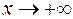
| 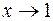
|
| б.б. | 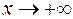
| 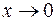
| 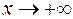
| 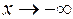
| 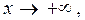 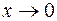
|
Так же как и б.б. последовательности, б.б. функции можно упорядочить по их порядку роста: при 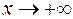
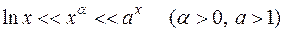 .
.
III Односторонние пределы
Рассмотрим функцию 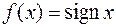 . Для произвольной б.м. последовательности
. Для произвольной б.м. последовательности 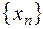 положительных чисел рассмотрим последовательность
положительных чисел рассмотрим последовательность 
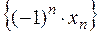 . Как произведение ограниченной на б.м., она сходится к нулю. Соответствующая последовательность значений функции
. Как произведение ограниченной на б.м., она сходится к нулю. Соответствующая последовательность значений функции 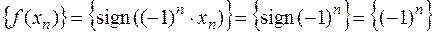 не имеет предела. Это означает, что
не имеет предела. Это означает, что 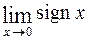 не существует. Однако,
не существует. Однако, 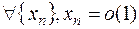 и
и 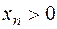 имеем
имеем 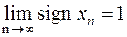 , а для
, а для 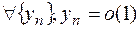 и
и 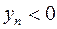 -
- 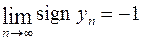 .
.
Такая ситуация характерна для многих функций, у которых нет предела в какой-либо точке, что и привело к появлению понятия односторонних пределов.
Определение 5. Пусть
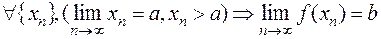 .
.
Тогда число  называют правым пределом (пределом справа или правосторонним пределом) функции
называют правым пределом (пределом справа или правосторонним пределом) функции 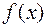 в точке
в точке 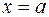 и пишут:
и пишут: 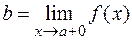 или
или 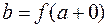 .
.
Определение левого предела аналогично, только требование 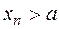 заменяют требованием
заменяют требованием 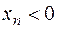 . Обозначения:
. Обозначения:
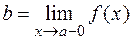 или
или 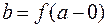 .
.
Если 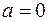 , то иногда вместо
, то иногда вместо 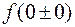 пишут
пишут 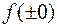 . Например,
. Например, 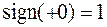 ,
, 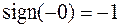 .
.
Сформулируем теорему, на которой базируется использование односторонних пределов.
Теорема 3. Для существования предела 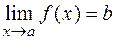 необходимо и достаточно существования порознь и равенство односторонних пределов:
необходимо и достаточно существования порознь и равенство односторонних пределов: 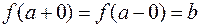 .
.
IV Теоремы о пределах функций
Теорема 4. Пусть у функции 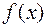 существует
существует  . Тогда в некоторой окрестности точки
. Тогда в некоторой окрестности точки 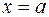 (за исключением, быть может, самой точки
(за исключением, быть может, самой точки 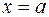 )
) 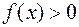 . Более того,
. Более того, 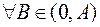
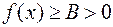 .
.
Теорема 5. Пусть у функции 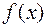 существует конечный предел при
существует конечный предел при  . Тогда в некоторой окрестности точки
. Тогда в некоторой окрестности точки 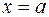 функция
функция 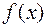 ограничена.
ограничена.
Теорема 6. Функция 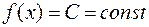 имеет предел в каждой точке числовой прямой, причем
имеет предел в каждой точке числовой прямой, причем 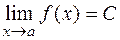 .
.
Теорема 7 (операции над пределами). Пусть функции 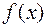 и
и 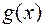 имеют в точке
имеют в точке 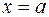 конечные пределы
конечные пределы  и
и 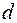 соответственно. Тогда в этой точке имеют конечные пределы и функции: 1)
соответственно. Тогда в этой точке имеют конечные пределы и функции: 1) 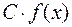 ; 2)
; 2) 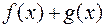 ; 3)
; 3) 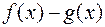 ; 4)
; 4) 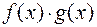 ; 5)
; 5) 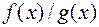 (при
(при 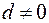 ). При этом имеют место следующие равенства:
). При этом имеют место следующие равенства:
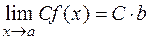 ,
,
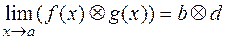 (здесь
(здесь 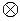 - символ арифметической операции).
- символ арифметической операции).
Для доказательства рассмотрим 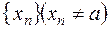 - произвольную последовательность значений аргумента, сходящуюся к
- произвольную последовательность значений аргумента, сходящуюся к 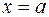 .
.
В силу существования пределов функций 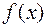 и
и 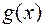 соответствующие последовательности значений функций
соответствующие последовательности значений функций 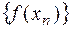 и
и 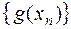 имеют пределы
имеют пределы  и
и 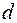 . Тогда, используя теорему 2 §7, получим, что последовательность
. Тогда, используя теорему 2 §7, получим, что последовательность 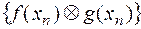 сходится к
сходится к 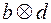 . Согласно определению предела функции это означает, что
. Согласно определению предела функции это означает, что 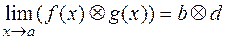 .
.
Теорема 8 (предельный переход в неравенствах). Пусть функции 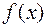 и
и 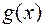 имеют в точке
имеют в точке 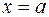 конечные пределы и в некоторой окрестности этой точки (за исключением, быть может, самой точки)
конечные пределы и в некоторой окрестности этой точки (за исключением, быть может, самой точки) 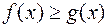 . Тогда и
. Тогда и 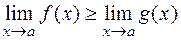 . В частности, если
. В частности, если 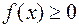 (
(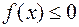 ), то и
), то и 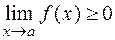 (
(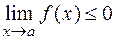 ).
).
Теорема 9. Если 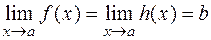 и в некоторой окрестности точки
и в некоторой окрестности точки 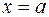 (за исключением, быть может, самой точки)
(за исключением, быть может, самой точки) 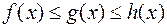 , то
, то 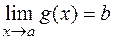 .
.
Теорема 10 (о замене переменной). Пусть хотя бы одна из функций 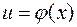 или
или 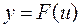 является строго монотонной и пусть существуют пределы
является строго монотонной и пусть существуют пределы 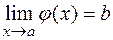 и
и 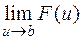 . Тогда и у сложной функции
. Тогда и у сложной функции 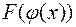 существует предел в точке
существует предел в точке 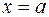 , причем
, причем
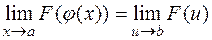 .
.
Теорема 11 (пределы элементарных функций). Пусть 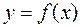 - элементарная функция и точка
- элементарная функция и точка 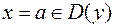 вместе с некоторой окрестностью. Тогда
вместе с некоторой окрестностью. Тогда 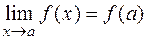 (в силу непрерывности элементарных функций).
(в силу непрерывности элементарных функций).
Теорема 12. Всякая ограниченная монотонная на промежутке функция имеет в каждой точке промежутка конечные односторонние пределы.
Пример 4.
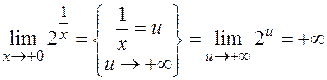 ,
,
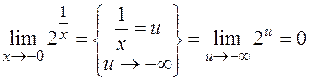 .
.
Пример 5.
а) 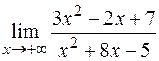 ; б)
; б) 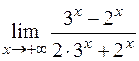 .
.
Путем деления числителя и знаменателя на самое быстрорастущее слагаемое, перейдем от б.б. функций к б.м. функциям и получим результат:
а) 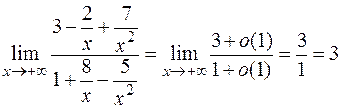 ;
;
б) 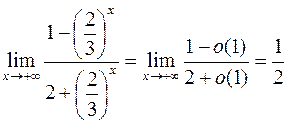 .
.
Замечание. Кроме определения предела функции на «языке последовательностей», существует (равносильное) определение предела функции на т.н. «языке 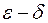 ». Некоторые из теорем о пределах удобнее доказывать именно на этом языке.
». Некоторые из теорем о пределах удобнее доказывать именно на этом языке.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1419; Нарушение авторских прав?; Мы поможем в написании вашей работы!