
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел последовательности
|
|
|
|
I Три определения
Определение 1. Число 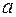 называют пределом последовательности
называют пределом последовательности 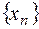 и пишут
и пишут 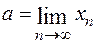 , если последовательность
, если последовательность 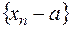 есть бесконечно малая.
есть бесконечно малая.
Используя определение 1 предыдущего параграфа, можно дать еще и такое определение предела.
Определение 2 ( язык« » ). Число
» ). Число 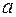 называют пределом последова- тельности
называют пределом последова- тельности 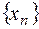 , если
, если
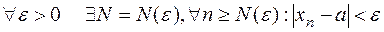 .
.
Последнее неравенство с модулем равносильно двойному неравенству 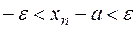 или
или 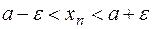 . Другими словами,
. Другими словами, 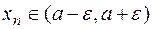 . Получаем еще одно определение предела.
. Получаем еще одно определение предела.
Определение 3 (язык «окрестностей»). Число 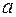 называют пределом последовательности
называют пределом последовательности 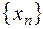 , если любая (сколь угодно малая)
, если любая (сколь угодно малая)  -окрестность числа
-окрестность числа 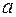 содержит все члены последовательности, начиная с некоторого номера, другими словами, вне такой окрестности содержится лишь конечное число членов последовательности
содержит все члены последовательности, начиная с некоторого номера, другими словами, вне такой окрестности содержится лишь конечное число членов последовательности 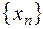 .
.
Замечания.
1. Из определений следует, что 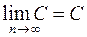 и
и 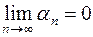 , если
, если  .
.
2. Если для последовательности 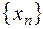 существует предел (в указанном выше смысле), то она называется сходящейся. В противном случае последовательность называется расходящейся. Примерами расходящихся последовательностей могут служить:
существует предел (в указанном выше смысле), то она называется сходящейся. В противном случае последовательность называется расходящейся. Примерами расходящихся последовательностей могут служить: 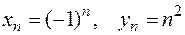 .
.
3. Определению 1 можно придать другую форму, более удобную в некото-рых случаях:
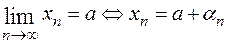 , где
, где  при
при 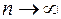 .
.
Такая форма позволяет найти предел такой, например, последовательности:
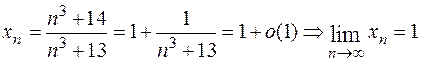 .
.
4. 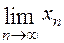 (если существует) не зависит от любого конечного числа членов последовательности
(если существует) не зависит от любого конечного числа членов последовательности 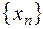 .
.
II Свойства сходящихся последовательностей и их пределов
1. Если последовательность сходится, то она ограничена (это свойство дока-зывается также, как аналогичное свойство б.м.)
2. Пусть  . Тогда:
. Тогда:
а) 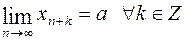 ;
;
б) 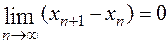 ;
;
в)  .
.
3. 
4. Если 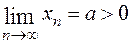 , то все члены последовательности
, то все члены последовательности 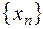 , начиная с некоторого номера, также положительны, и, более того, эти члены отграничены от нуля:
, начиная с некоторого номера, также положительны, и, более того, эти члены отграничены от нуля:  .
.
Для доказательства достаточно в определении 3 положить 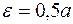 . Очевидно, что подобное свойство справедливо и для
. Очевидно, что подобное свойство справедливо и для 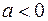 .
.
5. Если  и
и 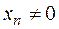 , то
, то  - ограничена.
- ограничена.
III Примеры вычисления пределов
1. 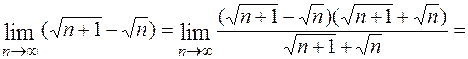
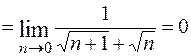 , ибо
, ибо 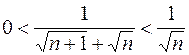 , а
, а 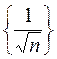 - эталонная б.м.
- эталонная б.м.
2. 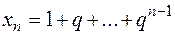 - это сумма
- это сумма 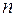 первых членов геометрической прогрессии
первых членов геометрической прогрессии  . Из элементарной математики известна формула для этой суммы
. Из элементарной математики известна формула для этой суммы
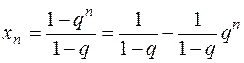 .
.
Если  , то
, то 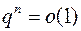 и
и 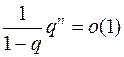 . Значит
. Значит 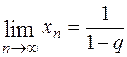 . Если
. Если 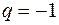 , то
, то 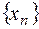 имеет вид: 1, 0, 1, 0, … и предела не имеет. Остальные случаи
имеет вид: 1, 0, 1, 0, … и предела не имеет. Остальные случаи 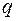 рассмотрим позже.
рассмотрим позже.
Задача (для самостоятельного решения). Пусть 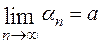 . Найти (если существуют) пределы следующих последовательностей: а)
. Найти (если существуют) пределы следующих последовательностей: а)  ; б)
; б)  ; в)
; в) 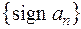 ; г)
; г) 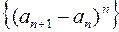 .
.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 541; Нарушение авторских прав?; Мы поможем в написании вашей работы!