Функции одной переменной: основные понятия

Основы возрастной педагогики

Белкин Август Соломонович

Учебное пособие

Редактор Л.И. Хлопова

Компьютерная верстка: Р.Ю. Волкова

Технический редактор Е.Ф. Коржуева

Корректоры Э.Г. Юрга, Л.Б. Орловская

Подписано в печать 23.06.2000. Формат 60 х 90/16. Гарнитура «Таймс».

Печать офсетная. Бумага газетная. Усл. печ. л. 12,0. Тираж 30000 экз. (1-й завод 1-10000 экз.). Заказ № 2701.

Лицензия ИД № 02025 от 13.06.2000. Издательский центр «Академия».

105043, Москва, ул. 8-я Парковая, 25. Тел./факс: [phone].

Отпечатано на Саратовском полиграфическом комбинате.

410004, г. Саратов, ул. Чернышевского, 59.

I Определение

Рассмотрим две переменные величины x и y. Если по некоторому правилу или закону каждому значению переменной величины x поставлено в соответствие одно определенное значение переменной величины y, то говорят, что y есть функция от x и пишут: y=f (x) или y=y (x).

Используемая терминология: x – аргумент, y – функция; x – независимая переменная, y – зависимая переменная.

В обозначении y=f (x) буква f является характеристикой функции и символизирует правило, о котором говорится в определении. Если рассматриваются разные функции, то их характеристики обозначаются разными буквами. И вообще, любая запись вида u=g (v) означает, что переменная u есть некоторая функция переменной v.

II Способы задания функции

Задать функцию означает задать правило (закон) соответствия. Наиболее употребительным является задание этого правила с помощью одной или нескольких формул, содержащих указание на те операции или действия над постоянными числами и над значениями аргумента x, которые необходимо произвести, чтобы получить соответствующее значение функции y. При этом различают три варианта этого т.н. аналитического способа задания:

1) явный, например, 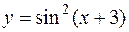или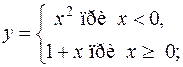

2) неявный, например, (переменные x и y связаны некоторым уравнением вида F (x, y) = 0);

3) параметрический, например, 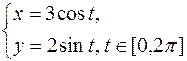(переменные x и y заданы как явные функции вспомогательной переменной – параметра t).

На практике часто используют табличный способ задания функции, когда задаются таблица отдельных значений аргумента и соответствующих им значений функции. Существуют методы позволяющие вычислить (приближенно!) значения функции, соответствующие промежуточным значениям аргумента, а также подобрать формулу, задающую функцию с определенной точностью.

Весьма распространенным, особенно в экспериментальных науках, является графический способ задания функции, при котором соответствие между аргументом и функцией задается посредством некоторой линии в системе координат xOy.

Используют в математике и словесный способ задания, когда функция описывается правилом её составления. Такова, например, функция y =[ x ]: “ есть целая часть x ”, т.е. наибольшее целое, не превосходящее числа x. Наряду с целой частью, рассматривают и функцию дробная часть числа: { x }= x- [ x ]. Примеры:

[2,8]=2, [-3,4]=-4, [2]=2.

III Область определения и область значения функции

Множество D (y) тех значений аргумента x, для которого определены соответствующие значения функции y=f (x), называют областью определения функции. При нахождении области определения функции, заданной аналитически, необходимо иметь в виду следующее:

1) если , то ;

2) если 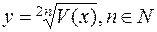, то ;

3) если , то ;

4) если 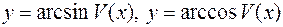, то .

Множество E (y) тех значений зависимой переменной , которые она принимает, когда зависимая переменная пробегает D (y), называют областьюзначений функции.

Для основных элементарных функций (см. ниже) области значений известны. В общем же случае для нахождения E (y) требуется исследование функции с помощью производных.

IV График функции

В математическом анализе функции графически не задают, но к графической иллюстрации прибегают всегда.

Графиком функции y=f (x) называют множество точек (координатной плоскости xOy) вида

.

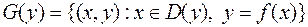В простых случаях график функции y=f (x) – это некоторая кривая, обладающая следующим свойством: любая прямая, параллельная оси ординат, пересекает эту кривую не более чем в одной точке. При этом запись y=f (x) называют уравнением этой кривой.

Существуют функции, графики которых изобразить невозможно. Примером может служить функция Дирихле:

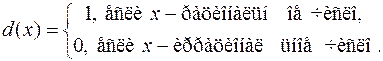
V Действия над функциями

Функция – это правило соответствия. Что же тогда означает, например, сумма двух правил f и g? Это новое правило (f+g), которое действует следующим образом: (f+g)(x)= f (x) +g (x). Аналогично определяются и остальные арифметические операции над функциями. Другими словами, все арифметические действия над функциями выполняются поточечно.

Кроме арифметических операций, имеется еще операция суперпозиции (наложения) функций, которая состоит в том, что вместо аргумента данной функции подставляется некоторая функция от другого аргумента. Например, суперпозиция функци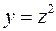й и дает функцию .

В общем случае, если y=F (z), а z=j (x), то переменная y, через посредство переменной z, сама является функцией от x: y=F (j (x)). Результат суперпозиции функций называется «функция от функции» или «сложная функция».

Следует подчеркнуть, что характеристика функции, как сложной, связана не с природой зависимости у от х, а лишь со способом задания этой зависимости. Например, пусть 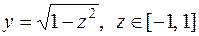, а , . Тогда 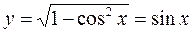. Здесь основная элементарная функция sin x оказалась заданной в виде суперпозиции двух функций.

Отметим, что в математическом анализе рассматриваются и другие операции над функциями, как то: предельный переход, дифференцирование, свертка и т.п. В таких операциях для вычисления значения функции-результата в одной точке мало знать значения функций-операндов в этой точке. Например, чтобы вычислить в точке x ₀, необходимо знать f (x) в некоторой окрестности этой точки.

VI Элементы поведения функции

К элементам поведения принято относить такие свойства функций как четность-нечетность, периодичность, монотонность и ограниченность.

1) Пусть область определения функции y=f (x) симметрична относительно нуля. Тогда: а) f (x) называется четной, если f (- x) =f (x); б) f (x) называется нечетной, если 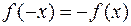(указанные соотношения должны выполняться для любого x из D (y)).

Примеры четных функций: y= cos x, y=x ² + 1, y=x sin x. Примеры нечетных функций: y= sin x, y=x ³, y=x ²tg x.

Графики четных и нечетных функций обладают полезным свойством – симметрией: график четной функции симметричен относительно оси ординат, а график нечетной симметричен относительно начала координат.

Любую функцию общего вида (т.е. не являющуюся ни четной, ни нечетной) можно представить в виде суммы четной и нечетной функции:

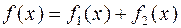, где 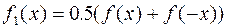- четная, а - нечетная.

2) Пусть область определения D (y) функции y=f (x) такова, что со всяким x из D (y), точки x+T и x-T также принадлежат D (y). Функция y=f (x) называется периодической, если для любого выполняется равенство 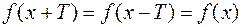. При этом число называется периодом.

Примерами периодических функций служат тригонометрические функции, а также y ={ x } – дробная часть числа x.

3) Если для любых двух значений аргумента x ₁, x ₂, принадлежащих промежутку | a, b | из неравенства x ₁ >x ₂ следует:

а) 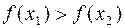, то f (x) называется возрастающей на | a, b |;

б) , то f (x) называется убывающей на | a, b |;

в) 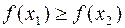, то f (x) называется неубывающей на | a, b |;

г) 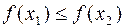, то f (x) называется невозрастающей на | a, b |.

Функции всех этих типов принято называть монотонными [в случаях а) и б) уточняют – «строго монотонные»]. Иногда удобно и неубывающую (невозрастающую) функцию называть возрастающей (убывающей) – но в широком смысле.

Примеры. а) y=x ² возрастает на (0, +¥) и убывает на (-¥, 0); б) y=x ³ всюду на R возрастает; б) y =arcсos x убывает на D (y) = [-1,1].

4) Если для любого из промежутка | a, b | существует число такое, что:

а) , то f (x) называется ограниченной сверху на | a, b |;

б) , то f (x) называется ограниченной снизу на | a, b |;

в) M> 0, , то f (x) называется ограниченной на | a, b |.

Примеры: а) y =arctg x – ограниченная; б) y= 2 ^x – ограниченная снизу.

VII Обратная функция

Функцию y=f (x) называют обратимой на промежутке | a, b |, если любое свое значение она принимает не более чем в одной точке этого промежутка; иными словами, если различным значениям аргумента соответствуют различные значения функции.

Пусть обратимая функция y=f (x) задана на промежутке | a, b | и пусть E (y)=| A, B |. Каждому y Î| A, B | поставим в соответствие то единственное значение x Î[ a, b ], для которого f (x) =y. Тем самым на | A, B | будет определена функция , которую называют обратной по отношению к функции y=f (x).

Отметим, что если - обратная для y=f (x), то и функция y=f (x) является обратной для . Поэтому, эти две функции часто называют взаимно обратными. Такие функции обладают очевидными свойствами:

.

Графики взаимно обратных функций совпадают. Можно, однако, потребовать, чтобы и аргумент обратной функции обозначался буквой x, т.е. вместо рассматривать функцию 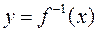. Графики такой пары функций y=f (x) и 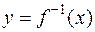симметричны относительно прямой y=x.

Можно доказать, что всякая строго монотонная функция имеет обратную, причем с тем же направлением монотонности.

Алгоритм нахождения обратной функции для функции y=f (x) следующий:

1) убедиться, что y=f (x) обратима (например, монотонная);

2) решить уравнение y=f (x) относительно x;

3) в полученном равенстве поменять местами x и y.

Пример. Найдем обратную функцию для функции (т.н. синус гиперболический).

а) Проверим монотонность. Пусть x ₁ >x ₂. Тогда .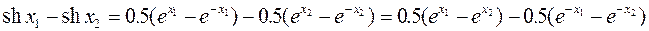

Функция y=e^x – возрастающая, поэтому разность в первой скобке положительна, а y=e^-x – убывающая, поэтому вторая разность – отрицательна. Значит , т.е , т.е. y= sh x – возрастающая функция, следовательно, обратимая.

б) Решим уравнение y= sh x относительно x:

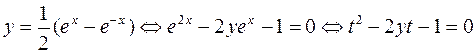
– не подходит, ибо

Итак, , т.е. .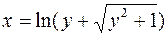

в) Поменяв местами x и y, получим искомую обратную функцию:

.

Дата добавления: 2014-11-08