
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентные б.м. и б.б. функции
|
|
|
|
I Сравнение б.м. и б.б. функций
Пусть 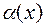 и
и 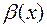 - пара б.м. или б.б. функций при
- пара б.м. или б.б. функций при  .
.
Определение 1. Если 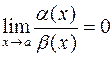 , то говорят, что при
, то говорят, что при  :
:
1) б.м. 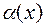 имеет более высокий порядок малости, чем б.м.
имеет более высокий порядок малости, чем б.м. 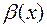 ;
;
2) б.б. 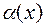 имеет более низкий порядок роста, чем б.б.
имеет более низкий порядок роста, чем б.б. 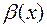 .
.
В обоих случаях пишут: “ 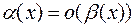 при
при  ”.
”.
Примеры.
1. 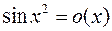 при
при 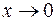 , ибо
, ибо 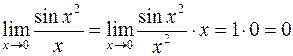 .
.
2. 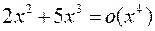 при
при 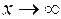 , ибо
, ибо  .
.
Отсюда получим, например,
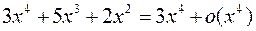 ,
, 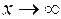 .
.
3. Известная цепочка соотношений 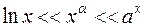 (
(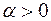 ,
, 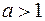 ) озна- чает, что при
) озна- чает, что при 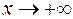
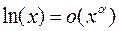 ,
, 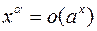 .
.
Замечание 1. Грубо говоря, соотношение 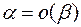 означает, что б.м.
означает, что б.м. 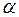 стремится к 0 быстрее, чем б.м.
стремится к 0 быстрее, чем б.м. 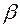 , а б.б.
, а б.б. 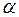 стремится к
стремится к 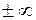 медленнее, чем б.б.
медленнее, чем б.б. 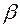 .
.
Определение 2. Если  , то говорят, что бесконечно малые
, то говорят, что бесконечно малые 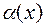 и
и 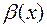 имеют одинаковый порядок малости, а бесконечно большие
имеют одинаковый порядок малости, а бесконечно большие 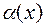 и
и 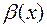 - одинаковый порядок роста при
- одинаковый порядок роста при  .
.
Определение 3. Если  не существует, то б.м. или б.б.
не существует, то б.м. или б.б. 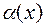 и
и 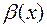 называют несравнимыми.
называют несравнимыми.
Примером несравнимых б.м. (при 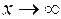 ) служат функции
) служат функции 
и 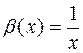 .
.
II Эквивалентные функции: два определения
Определение 4. Если 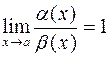 , то пару б.м. или б.б. функций
, то пару б.м. или б.б. функций 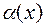 и
и 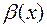 называют эквивалентными при
называют эквивалентными при  и пишут:
и пишут: 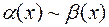 при
при  .
.
Примерами эквивалентных б.м. при 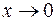 служат
служат 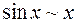 ,
,  ,
,  .
.
Приведем несколько свойств символа ~:
1) 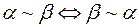 ;
;
2) 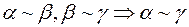 ;
;
3)  ;
;
4) 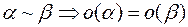 ;
;
5) 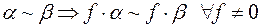 .
.
Замечание 2. Для упрощения применения эквивалентностей удобно пару любых функций называть эквивалентными, если предел их отношения равен 1 (иногда уточняют: «эквивалентные в широком смысле»).
Для б.м. функций можно дать еще одно определение эквивалентности (равносильное определению 4).
Определение 5. Бесконечно малые функции эквивалентны, если их разность есть б.м. более высокого порядка малости, чем каждая из них:
 и
и  .
.
III Таблица эквивалентностей
При 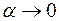 :
:
1) 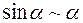 ; 2)
; 2) 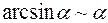 ; 3)
; 3)  ;
;
3)  ; 5)
; 5) 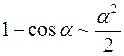 ; 6)
; 6) 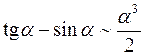 ;
;
7) 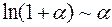 ; 8)
; 8) 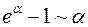 ; 9)
; 9) 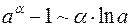 ;
;
10) 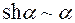 ; 11)
; 11) 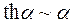 ; 12)
; 12)  ;
;
13) 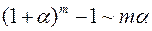 .
.
Кроме этих формул используются еще такие:
14) многочлен на 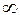 эквивалентен старшему члену, а в нуле - младшему;
эквивалентен старшему члену, а в нуле - младшему;
15)  при
при  , если только
, если только  и
и 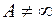 ;
;
16) 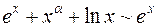 ,
, 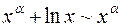 при
при 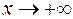 (
(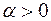 ,
, 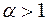 );
);
17) 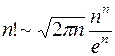 при
при 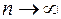 .
.
Часть этих формул была получена в §10. Выведем еще несколько других:
5) 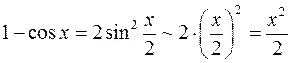 ;
;
10) 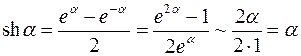 ;
;
13)  ;
;
15) Пусть  , Тогда
, Тогда 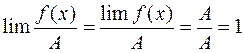 , т.е.
, т.е.
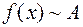 (в широком смысле).
(в широком смысле).
IV Использование эквивалентностей для вычисления пределов
Теорема. Пусть 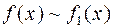 , а
, а 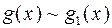 при
при  . Если
. Если 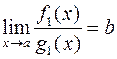 , то и
, то и 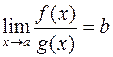 .
.
Доказательство.
 .
.
Практический вывод. При вычислении пределов частных и произведений функций каждую из них можно заменить эквивалентной.
Примеры.
4. 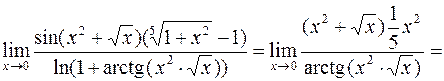
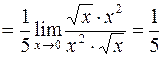 .
.
Здесь были использованы эквивалентности для синуса, логарифма, арктангенса, степенной функции и выражения типа многочлена (алгебраической суммы степеней переменной с неотрицательными показателями, а не только натуральными, как в обычном многочлене).
5. Вычислим предел 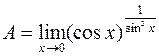 . Используя основное логариф-мическое тождество, свойство логарифма степени и непрерывность функции
. Используя основное логариф-мическое тождество, свойство логарифма степени и непрерывность функции 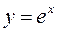 , получим:
, получим:
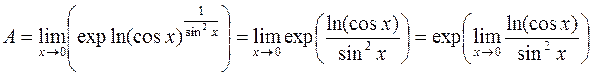 .
.
Выведем нужную здесь формулу эквивалентности при 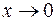 :
:
 .
.
Итак, 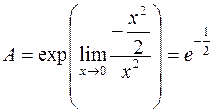 .
.
6. Приведем ряд примеров «подгонки» под табличную форму эквивалент-ности:
 при
при 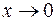 ;
;
 при
при 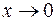 ;
;
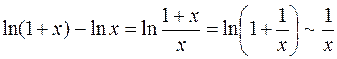 при
при 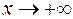 .
.
Замечание-предостережение. Использовать эквивалентности (в указанной форме 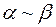 ) в суммах, разностях функций и под знаками функций, вообще говоря, нельзя. Исключение составляет степенная функция, т.е., если
) в суммах, разностях функций и под знаками функций, вообще говоря, нельзя. Исключение составляет степенная функция, т.е., если 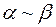 , то
, то 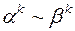 ,
, 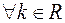 .
.
Однако, существует другая форма эквивалентностей, которую можно использовать везде. Эту форму рассмотрим в следующей части параграфа.
V Асимптотические формулы
В силу второго определения эквивалентности соотношения 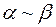 равносильно
равносильно 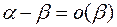 или
или 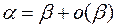 . Таким образом, таблицу эквивалентностей можно записать в форме т.н. асимптотических формул. Приведем лишь некоторые из них. Все остальные студенты должны уметь выводить самостоятельно.
. Таким образом, таблицу эквивалентностей можно записать в форме т.н. асимптотических формул. Приведем лишь некоторые из них. Все остальные студенты должны уметь выводить самостоятельно.
Итак, при 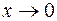 :
:
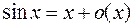 ,
, 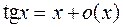 ,
,
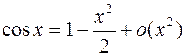 ,
, 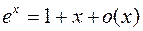 ,
,
 ,
, 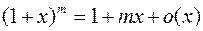 .
.
Эти асимптотические формулы можно применять в суммах, разностях и под знаками функций. Однако, не всегда они дают ответ на поставленный вопрос.
Примеры.
7. 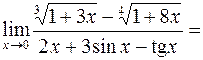
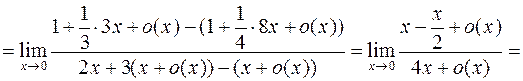
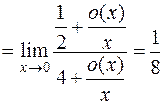 .
.
Здесь использован тот факт, что по определению символа  имеем:
имеем: 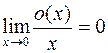 .
.
8. 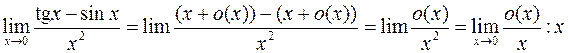 = – частное бесконечно малых может быть любым. Такая ситуация означает, что соответствующая асимптотическая формула недостаточно точная. В теме «Формулы Тейлора и Маклорена» будут даны уточнения:
= – частное бесконечно малых может быть любым. Такая ситуация означает, что соответствующая асимптотическая формула недостаточно точная. В теме «Формулы Тейлора и Маклорена» будут даны уточнения:
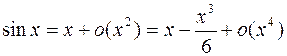 ,
, 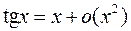 .
.
Задача. Вычислить пределы:
а) 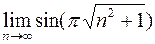 ; б)
; б) 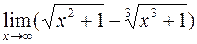 .
.
Лекция 7
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 3857; Нарушение авторских прав?; Мы поможем в написании вашей работы!