
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементарные функции
|
|
|
|
I Основные элементарные функции
 К основным элементарным функциям относят константы, степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.
К основным элементарным функциям относят константы, степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.
1) Константы y = Const.
D (y) = R, E (y) = { c }.
 не существует, четная.
не существует, четная.
График – прямая, параллельная оси абсцисс.
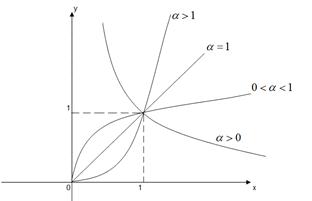 2) Степенные
2) Степенные  .
.
D (y)и E (y)зависят от a, но " a (0, + ¥)Ì D (y).
Четность-нечетность зависит от a.
Обратная для  есть
есть  .
.
Для a< 0оси координат – асимптоты.
3) Показательные 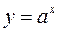 (0< a ¹1).
(0< a ¹1). 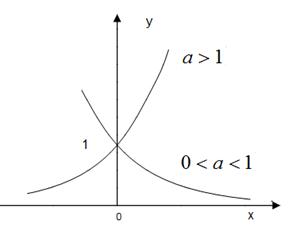
D (y) = R, E (y) = (0, + ¥).
Функция общего вида.
Ось абсцисс – асимптота.
Обратная для функции 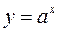 есть логарифмическая функция
есть логарифмическая функция 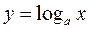 .
.
4) 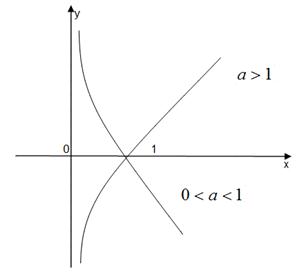 Логарифмическая
Логарифмическая 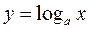 (0<a¹1).
(0<a¹1).
D (y) = (0, + ¥), E (y) = R.
Функция общего вида.
Ось ординат – асимптота.
Обратная для логарифмической – показательная функция.
В математическом анализе в основном используют натуральные логарифмы ln x, т.е. логарифмы с основанием a=e= 2,7…
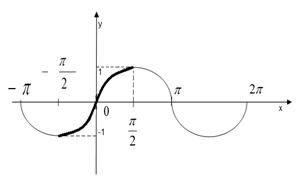 5) Тригонометрические
5) Тригонометрические
а)  .
.
D (y) = R, E (y)= [-1, 1].
Нечетная.
Периодическая,  .
.

б)  .
.
D (y) = R, E (y) = [-1, 1].
Четная.
Периодическая,  .
.
 в)
в) 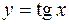 .
.
D (y) = R \ {  , kÎZ },
, kÎZ },
E (y) = R.
Нечетная.
Периодическая, 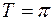 .
.
Прямые 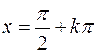 - асимптоты.
- асимптоты.

г)  .
.
D (y) = R \ { kp, kÎZ }, E (y) = R
Нечетная.
Периодическая, 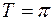 .
.
Прямые x = kp - асимптоты.
6) Обратные тригонометрические
При определении этих функций выбираются следующие участки монотонности: для синуса - 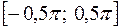 , для косинуса - [0, p ], для тангенса -
, для косинуса - [0, p ], для тангенса -  , для котангенса - (0, p).
, для котангенса - (0, p).
Определение, например, арксинуса:
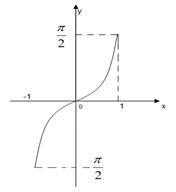 arcsin a – это угол a Î
arcsin a – это угол a Î 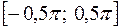 такой, что sina= a. Остальные функции определяются аналогично.
такой, что sina= a. Остальные функции определяются аналогично.
а)  .
.
D (y) = [-1, 1], E (y) = 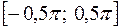 .
.
Нечетная.
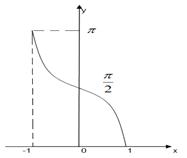 б)
б) 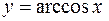 .
.
D (y) = [-1, 1], E (y) = [0, p ].
arccos(-x) = p - arccos x.
arcsin x + arccos x = 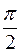 .
.

в)  .
.
D (y) = R, E (y) =  .
.
Нечетная.
Прямые  - асимптоты.
- асимптоты.
 г)
г) 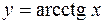 .
.
D (y) = R, E (y) = (0, p).
arcctg(-x) = p - arcctg x.
Прямые y = 0 и y = p - асимптоты.
Замечание. Иногда к основным элементарным функциям относят еще и т.н. гиперболические функции и обратные к ним. Все эти функции достаточно просто выражаются через показательную и логарифмическую функции.
а) синус гиперболический  : D (y) = R, E (y) = R, нечетная; обратная функция имеет вид y = Arsh x =
: D (y) = R, E (y) = R, нечетная; обратная функция имеет вид y = Arsh x = 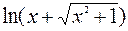 .
.
б) косинус гиперболический 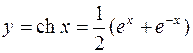 : D (y) = R, E (y) = [1, +¥), четная; обратная функция имеет вид y = Arch x =
: D (y) = R, E (y) = [1, +¥), четная; обратная функция имеет вид y = Arch x =  ,
, 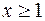 (у функции ch x берется ветвь
(у функции ch x берется ветвь  ).
).
в) тангенс и котангенс гиперболические определяются так же как и в тригонометрии:
 ,
,  .
.
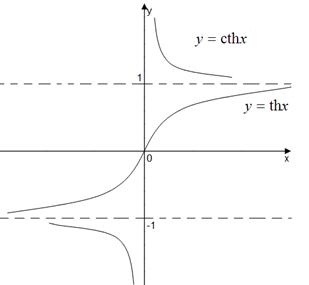
Обратная функция для y = th x – это y = Arth x =  . Графики гиперболических функций:
. Графики гиперболических функций:

II Элементарные функции
Определение. Элементарной называют функцию, которая может быть задана явно одной формулой, содержащей конечное число арифметических операций и суперпозиций, примененных к основным элементарным функциям.
Следует отметить, что некоторые функции, заданные несколькими формулами (т.е., вообще говоря, неэлементарные) иногда удается записать одной формулой. Примером служит функция y = | x |. По определению
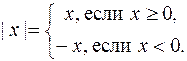
В то же время имеем: 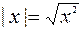 . Таким образом, функция y = | x | - элементарная. Ее график:
. Таким образом, функция y = | x | - элементарная. Ее график:
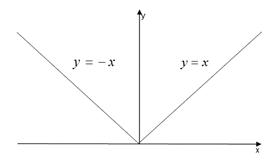
 III Примеры неэлементарных функций
III Примеры неэлементарных функций
1) 
(читается «у равно сигнум х»).
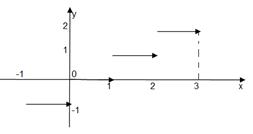 2) y = [ x ], где [ x ] - целая часть числа x
2) y = [ x ], где [ x ] - целая часть числа x
(читается «y равно антье x»).
Эта функция неэлементарная, ибо задается не формулой, а словесно:
[ x ] - наибольшее целое, не превосходящее x.
Отметим одно свойство:  .
.

3) y = { x }, где { x }-дробная часть числа x, т.е. { x } = x - [ x ].
Лекция 2
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 4449; Нарушение авторских прав?; Мы поможем в написании вашей работы!