О моделях выхода из мальтузианской ловушки и возможностях их дальнейшего развития

Модели, специально посвященные анализу выхода из мальтузианской ловушки (Artzrouni, Komlos 1985; Steinmann, Komlos 1988; Komlos, Artzrouni 1990; Steinmann, Prskawetz, Feichtinger 1998; Wood 1998; Kögel, Prskawetz 2001), обладают следующими особенностями:

· используется макроподход, в обобщенном виде описывающий демографическую динамику больших регионов (или мира в целом) и динамику сельскохозяйственного производства на больших временных интервалах (столетия и тысячелетия);

· при описании динамики производства используется функция типа Кобба – Дугласа с учетом технологического развития, темпы которого считаются зависящими от общего количества населения.

Результаты моделирования заключаются в том, что при определенном уровне технологического развития динамика производства начинает опережать динамику демографического роста, тем самым обеспечивая выход из мальтузианской ловушки. Хотя
математический аппарат рассматриваемых моделей довольно сложен (см., например, описание математического аппарата модели Арцруни – Комлоса [Artzrouni, Komlos 1985]
в Гринин, Коротаев 2010 а), получаемый общий вывод весьма предсказуем на основе лишь логических рассуждений. Более детальное моделирование для конкретных стран с учетом реальных исторических условий в рассматриваемых работах (Artzrouni, Komlos 1985; Steinmann, Komlos 1988; Komlos, Artzrouni 1990; Steinmann, Prskawetz, Feichtinger 1998; Wood 1998; Kögel, Prskawetz 2001) не проводилось, что обусловлено обобщенным характером используемого макроподхода.

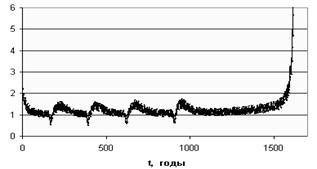
Одним из авторов данной работы было предложено несколько матема­тических моделей, описывающих как взаимодействие трендовой и цикли­ческой динамики в аграрных и раннеиндустриальных обществах, так и выход из мальтузианской ловушки (Коротаев 2006; Коротаев, Комарова, Халтурина 2007). При этом был получен целый ряд интересных результа­тов, позволивших приступить к изучению взаимодействия исторической трендовой и циклической динамики. Так, числовой анализ предложенных моделей помог выявить и объяснить тенденцию к росту продолжительности социально-демогра-фических циклов накануне выхода из мальтузианской ловушки, а также феномен исчезновения социально-демографических циклов после выхода из мальтузианской ловушки. Была также выявлена зависимость скорости выхода из мальтузианской ловушки от характерного периода циклов: чем короче этот период, тем больше времени уходит у соответствующей системы на выход из данной ловушки. Выявлен был и феномен длительной стагнации душевого потребления рядового населения накануне выхода из мальтузианской ловушки (Там же) (см. Рис. 2.1.9; см. также Коротаев, Комарова, Халтурина 2007: 165, Диаграмма 4.25).

Рис. 2.1.9. Динамика, генерируемая компактной трендо-циклической моделью: производство продукта на душу населения (в МГП[10])

Большой интерес представляет и полученное математическое описание динамики внутренней военной активности накануне и после выхода из мальтузианской ловушки,
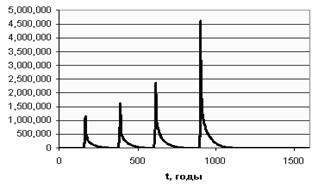
показывающее максимальный всплеск этой ак­тивности как раз накануне выхода (см.
Рис. 2.1.10; см. также Коротаев, Комарова, Хал­турина 2007: 166, Диаграмма 4.26).

Рис. 2.1.10. Динамика внутренней военной активности, генерируемая компакт-ной трендо-циклической моделью (внутренняя военная активность измеряется как число «крестьян», гибнущих за год от рук «бандитов»)

Дата добавления: 2014-11-18