Покорный Ю.В., Зверева М.Б., Перловская Т.В

П 485 О некоторых натуральных одномерных краевых задачах: Научно-методическое пособие. – Воронеж, 2007. –37с., библ. 13.

ISBN 5-7458-1125-0

Пособие раскрывает математический генезис разнообразных нестандартных краевых задач, возникающих при моделировании упругих деформаций систем одномерных континуумов. Описываемые методы корректно обосновывают условия сочленения (трансмиссии).

Рассчитано на студентов, аспирантов и заинтересованных специалистов, не удовлетворенных интуитивно-наглядными мотивациями в серьезных задачах.

ISBN 5-7458-1125-0 © Ю.В. Покорный, 2007

Возможно, в это трудно поверить, что математической моделью де­формаций однородной струны, «испорченной» в одной точке

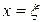упругой подпоркой (пружиной) будет обычное для струны уравнение (струна предполагается натянутой вдоль отрезка )

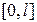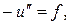(1)

(здесь порождается внешней силой) с обычными условиями закрепления концов

(2)

но с одной существенной оговоркой, а именно – уравнение (1) справедливо не на всем отрезке 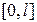, а с исключенной точкой 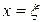, т.е. на каждом полуинтервале 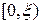и 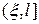. А в этой точке помимо условия непрерывности

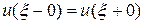(3)

должно выполняться и еще одно условие

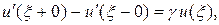(4)

учитывающее упругую реакцию пружины.

Совсем до недавних времен эта простая физически ситуация не вкладывалась в стандартные теории для обыкновенных дифференциальных уравнений (ОДУ) и не встречалась на страницах не только учебников, но и монографий. Согласно традициям учебной математики задачу (1)-(4) нельзя относить к краевым задачам, где дополнительные к уравнению условия являются граничными, т.е. заданы в граничных точках, ибо точка 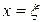явно не граничная.

С другой стороны, если опираться на такую науку, как теория обобщенных функций, то моделью данной физической задачи может служить уравнение

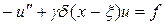(5)

при условиях (2). В (5) через 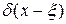обозначена так называемая дельта-функция, которая по мнению физиков есть производная от функции Хевисайда

т.е. производная от скачка.

Об адекватности обоих описаний одной и той же задачи можно судить, если опереться на классические вариационные принципы физики, весьма эффективно объясняющие все математические особенности подобных «негладких» математических моделей. Проводимый ниже разговор в этом направлении позволит выяснить, что для обыкновенных дифференциальных уравнений второго порядка краевая задача (т.е. задача с условиями на концах) гораздо более физична, чем привычная из ОДУ задача Коши.

Содержание

§1. Краевая задача – курьез для ОДУ?! 6

§2. Как в математику вошли краевые задачи. 7

§3. Уравнение Эйлера. 10

§4. Задача о брахистохроне. 16

§5. Задача о струне. 18

§6. Задача Больца. 24

§7. Задача Пуассона. 25

§8. Задача о стержне. 27

§9. Функция Грина. 32

Литература. 37

§1. Краевая задача – курьез для ОДУ?!

В университетском курсе «Обыкновенные дифференциальные уравнения» (сокращенно – ОДУ) речь идет о за­дачах, возникающих в механике материальной точки, когда неизвестная функ­ция y(x) имеет скалярный аргумент, со времен Ньютона отождествляемый со временем. Поэтому естественна да и понятна наиболее общая для приложений форма за­писи уравнения в виде

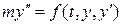, (1.1)

где левая часть отождествляется с силой инерции (иногда левая часть так и записывается в виде 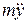), а правая часть интерпретируется как внешняя сила, действующая на рассматриваемую материальную точку. В более об­щих ситуациях уравнение (1.1) описывает не скалярнозначную, а векторно­значную функцию 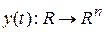– это в случае, когда рассматриваемая сис­тема имеет n скалярных параметров и может отождествляться с точкой в n - мерном пространстве R 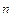. Как в первой, простейшей скалярной, так и во второй – векторной интерпретации конкретное решение уравнения однозначно определено, если дополнительно заданы так называемые начальные условия – в какой-то «начальный момент времени 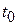» задано состояние объекта 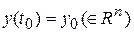и его скорость 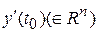. Разрешимость урав­нения (1.1) при таких начальных условиях

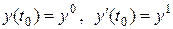
является в теории обыкновенных дифференциальных уравнений наиболее принципиальным фактом, которому посвящены наиболее трудные теоремы (Коши, Пеано и проч.).

Выпячивание в курсе ОДУ начальной задачи – чисто методическая традиция, отражающая исторический ход развития теории ОДУ. Весь 18в. анализ бесконечно малых, только что созревший в конце 17в., был поставлен на службу задач механики и, в первую очередь – задач небесной механики, где решающую роль играло уравнение (1.1), переписывающее в символьной форме закон Ньютона. Причем существование решения и его качественные свойства (типа устойчивости) тогда и не обсуждались – они были актуализированы лишь в конце 19в., когда внедрение новой математики (опирающееся на дифференциальное исчисление) в механику уже было завершено.

Возможность замены начальных условий на какие-либо другие, дополнительные к (1.1) в теории ОДУ обычно даже не обсуждается. Иногда вскользь возникает так называемая задача Штурма – Лиувилля

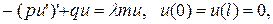
но ее роль в естествознании обсуждается только в специальной литературе отдельно от теории ОДУ и от натурального генезиса.

Дата добавления: 2014-11-18