Как в математику вошли краевые задачи

Развитие естествознания в конце 18 – начале 19 веков потребовало пе­рехода от анализа задач механики к анализу более сложных объектов, кото­рые уже не могли описываться конечным числом параметров. Одним из первых внешне совсем простых, а по существу – совершенно нетривиальных объектов с бесконечным числом (континуумом) параметров была струна. Магические свойства этого внешне тривиального объекта приковывали внимание еще древних греков. В особенности – Пифагора, обнаружившего математические связи между благозвучными сочетаниями колебаний струны.

К концу 18 века уже стало ясно, что звучание однородной струны подчиняется уравнению

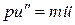, (2.1)

где u = u(x,t) – форма струны в момент времени t, если считать, что в состоянии покоя она была растянута вдоль отрезка [0,l] оси Ох. Штрихи здесь означает производные по длине 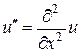, а точки вверху (ньютоновское обозначение) – производные по времени, т.е. 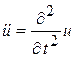. И вот оказалось, что для однозначности определения реальной формы струны необходимы четыре дополнительных условия. По времени – как бы для ОДУ условия начального типа, т.е.

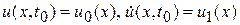, (2.2)

а по физическим, т.е. пространственным соображениям вместо двух условий на одном (например – левом) конце обязательно должны были присутствовать два условия на двух разных концах

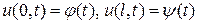. (2.3)

Эти условия шли как бы из физики, из натуры, от физической интуиции и с чисто математической точки зрения не очень обсуждались – на тему, а нельзя ли их взять да и заменить двумя условиями на левом конце? Позднее этот вопрос, для физиков крамольный, математиками оказался как бы забытым.

Мы с Вами, дорогой Читатель, этот далеко не праздный вопрос запомнили. Именно он объясняет, почему математика не имеет права даже в ОДУ ограничиваться только начальными задачами.

Уже в момент появления уравнения (2.1), ставшего как бы элементом физического фольклора, мотивация его была чисто интуитивной, а именно, левая часть его отвечает как бы за упругую реакцию элемента струны, а правая – за силу инерции того же элемента.

Первый, кого такой разговор не удовлетворил, был Даламбер. Он заметил, что если струна неоднородна, то величина 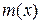– не собственно масса, а локальная плотность масс – если через 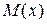обозначить массу куска струны от 0 до x, то 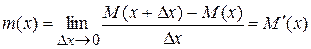– величина, физически имеющая даже не ту, что просто масса, размерность. Даламбер предложил обозначить правую часть (2.1), имевшую характер силы, через f(t) и предположил, что в каждый фиксированный момент t уравнение

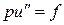(2.4)

с условиями

u(0) = 0, u(l) = 0

имеет некое решение , связанное с 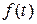. Эту связь он записал в виде

.

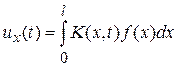Считая, что сила инерции элемента длины dx (от х до x+dx) с массой mdx определяется величиной m 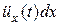, откуда

,

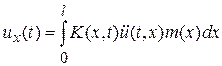и он получил .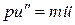

Эти весьма нетривиальные соображения Даламбера станут для нас прозрачными, когда мы освоим элементы теории краевых задач. Заметим и роль в них интегральных уравнений. Но это – позднее.

Таким образом, уже здесь существенной оказалась для уравнения (2.1) не одноточечная задача с двумя условиями на одном конце, а задача с двумя условиями на обоих концах. Далее мы обнаружим, что для физических задач наличие условий на концах – своего рода закон природы. И что задача Коши – чисто теоретическая задача в ОДУ, а для описания реальных процессов с континуальными объектами – даже в рамках ОДУ она (задача Коши) – скорее понятие, чем условие.

К середине 19 века было обнаружено (в основном физиками), что большинство дифференциальных уравнений, возникающих в физических процессах и явлениях, имеют вариационную природу. Точнее – они подчиняются вариационным принципам, которые являются своего рода физической аксиомой и в наиболее простой форме звучат так:

Дата добавления: 2014-11-18