Задачи. Найдите допустимые экстремали (т.е

Упражнения.

Найдите допустимые экстремали (т.е. решения уравнения Эйлера – Пуассона, удовлетворяющие указанным условиям) для заданных функционалов:

7.1.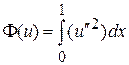

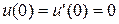
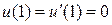
7.2. , , ,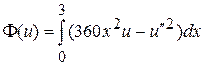

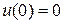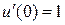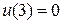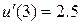
7.3 , , , .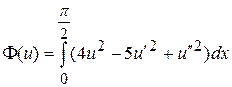

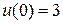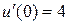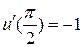З.7.1. Получите необходимое условие экстремума для функционала (7.1) без условий (7.2) на правом конце.

З.7.2. Получите необходимое условие экстремума для функционала (7.1) без части условий на правом конце.

З.7.3. Сформулируйте аналог задачи Больца, получите необходимое условие экстремума.

§8. Задача о стержне.

Предположим, что рассматриваемый стержень деформируется в вертикальной плоскости и расположен вдоль отрезка [0,1] оси Ox. Применяя соображения Эйлера, предположим стержень расслоенным по вертикали на элементарные плоские слои. Существует (это стандартное предположение) слой, который при деформациях не меняет своей длины ни на каком участке. Этот слой называют нейтральным. Пересечение нейтрального слоя с продольным сечением балки образует нейтральную линию. Отклонение нейтральной линии от положения равновесия называют деформацией стержня. При изгибе стержня слои, отличные от нейтрального, локально растягиваются или сжимаются, сопротивляясь по закону Гука (линейной упругости) и накапливая за счет этого энергию изгиба. Предполагая деформации малыми, для прояснения сути проведем рассуждения в терминах малых элементов, опуская малые старших порядков.

Мы считаем деформации стержня непрерывными функциями, заданными на отрезке [0,1]. Пусть u(x)– форма нейтральной линии (деформации), принятая под воздействием на элемент [x,x+dx) внешней силы f(x)dx. Работа, выполняемая этой силой при перемещении нашего элемента на дистанцию u(x), равна u(x)f(x)dx. В целом вдоль всего стержня затрачивается энергия

.

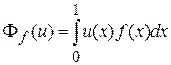Полная энергия 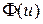, накапливаемая стержнем под воздействием внешней нагрузки, определяется еще дополнительным слагаемым 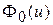, описывающим изгибную энергию стержня. Подчеркнем, что рассматриваемая функция u(x) – это гипотетическая (виртуальная) деформация. Реальная деформация должна давать минимум

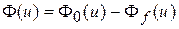
Пусть 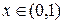. Для нулевой деформации стержня промежуток по вертикали, занимаемый стержнем, обозначим через 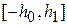, считая от нейтральной линии. Рассмотрим элементарный слой между h и h+dh, обозначая через dS(h) площадь поперечного сечения этого слоя. За S(h) здесь может быть принята площадь поперечного сечения стержня в точке x между уровнями от 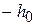до . Рассматривая кусок стержня на сегменте 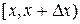, мы у этого слоя будем иметь начальную длину 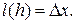Сопротивление растяжению или сжатию этот слой оказывает по закону Гука с силой, равной kdl(h). Здесь dl(h) – удлинение рассматриваемого слоя и k – коэффициент упругости, равный

,

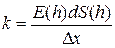где E(h) – модуль Юнга материала слоя. Работа по преодолению линейной силы 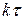на промежутке 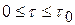равна 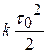. Поэтому энергия dV(h), накапливаемая элементарным слоем (уровня h) при изменении длины на dl(h), равна

.

Найдем удлинение dl(h) нашего слоя. Оно определяется его расстоянием h

от нейтральной линии и углом 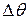между поперечными сечениями в точках x и 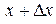. С точностью до малых более высокого порядка 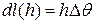, в силу чего энергия, накапливаемая элементарным слоем на уровне h, равна

.

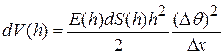Интегрирование последней величины по толщине балки, т.е. по h, в пределах

от 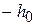до , приводит к энергии изгиба , накапливаемой куском балки на участке 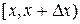. Она определяется величиной

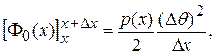(8.1)

где положено

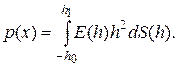
Угол между нормалями совпадает с углом между касательными, тангенсы углов наклона которых есть 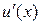и 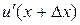. Поэтому 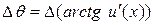, что означает 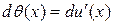. Последнее приводит (8.1) к виду

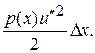
Следовательно, изгибная энергия стержня

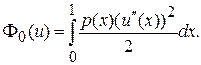
Таким образом, для полной энергии стержня, деформированного под влиянием внешней нагрузки, мы для виртуальной деформации u(x) имеем

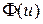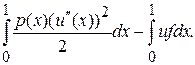= (8.2)

Дата добавления: 2014-11-18