Функция Грина

Пусть на отрезке [0,l] задана двухточечная краевая задача, определяемая линейным уравнением

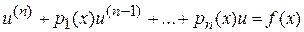(9.1)

с непрерывными коэффициентами и n краевыми условиями

(9.2)

с функционалами 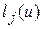вида

(9.3)

Теорема 9.1. Для того чтобы краевая задача (9.1)-(9.2) была однозначно разрешимой для любой правой части f(x) и любого набора значений 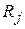, необходимо и достаточно, чтобы однородная задача (, 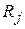=0 )имела только тривиальное решение .

Доказательство основывается на представлении общего решения (9.1) в виде

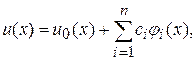(9.4)

где – фундаментальная система решений однородного уравнения, а – произвольное частное решение неоднородного уравнения. Подстановка (9.4) в условия (9.2) дает систему линейных алгебраических уравнений с матрицей 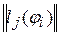, так что утверждение теоремы эквивалентно отличию от нуля детерминанта det .

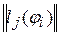Эта теорема делает полезным следующее определение.

Определение 9.1. Задачу (9.1)-(9.2) назовем невырожденной, если соответствующая однородная задача имеет только тривиальное решение.

Всюду далее мы будем предполагать невырожденность рассматриваемой задачи.

Для простоты фундаментальную систему решений мы будем выбирать так, чтобы она оказалась биортогональной набору функционалов 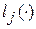. Эта система будет ниже обозначаться через 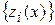, так что 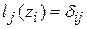( 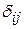-символ Кронекера, т.е. 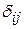=0 при , и 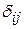=1 при ). Заметим, что существование такой системы следует из невырожденности рассматриваемой задачи. Тогда решение краевой задачи выписывается явно:

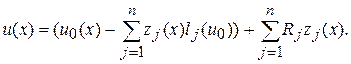(9.5)

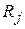Эта формула представляет решение в виде суммы решений полуоднородных задач: одной с при f(x) из (9.1), и другой – с при ненулевых . Что касается второй группы слагаемых в (9.5), то мы к ней далее возвращаться не будем. В центре нашего внимания будет первое слагаемое. Поэтому далее мы будем рассматривать только однородные условия

(9.6)

Определение 9.2. Функцией Грина задачи (9.1)-(9.6) будем называть любую функцию G(x,s), позволяющую получить решение задачи (9.1)-(9.6) в виде

(9.7)

Теорема 9.2. Для любой невырожденной задачи (9.1)-(9.6) функция Грина существует.

Доказательство состоит попросту в выражении 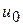в формуле (9.5) через f(x). Это можно сделать, например, с помощью функции Коши

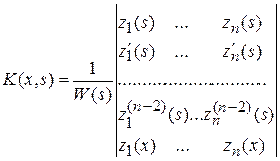, (9.8)

где

в виде

(9.9)

Желая привести фигурирующий здесь интеграл с переменным верхним пределом к интегралу с постоянными пределами вида (9.7), представим (9.9) в виде

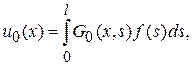(9.10)

где обозначено

(9.11)

На диагонали x=s, очевидно, , поэтому включение значения x=s и в ту, и в другую строку не приводит к противоречиям. Подставляя (9.10) в (9.5), получаем

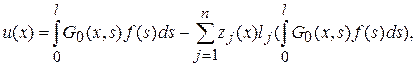(9.12)

так что вопрос о представлении 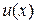в форме (9.7) упирается только в возможность перестановки функционалов под знак интеграла.

Вообще говоря, такая перестановочность имеет место в силу свойств функции Коши: так как при i=0,….,n-2, то из (9.9) следует

(i=0,….,n-1),

и потому для функционала 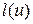вида (9.3)

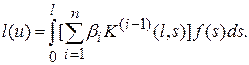
Обозначая здесь сумму в квадратных скобках через 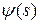(для 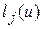соответственно через ), из (9.12) получаем

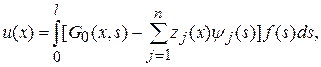
что не только доказывает теорему, но и предъявляет G(x,s) явно

,

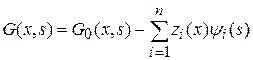или, в более «классической форме»,

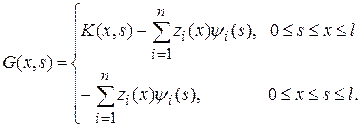
Следствие 1. 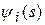непрерывны на [0,l].

Следствие 2. G(x,s) непрерывна вместе со своими производными по x до порядка n в каждом треугольнике 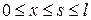и 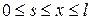вплоть до границы.

Следствие 3. Непрерывная функция G(x,s),дающая представление решения в виде (9.7), единственна.

Следствие 4. Для любого фиксированного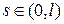

Следствие 5. Для любого фиксированного 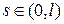и любого 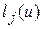из условий (9.3),

Следствие 6. Для любого фиксированного 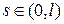функция G(x,s) является решением однородного уравнения (9.1) на [0,s] и на [s,l].

Дата добавления: 2014-11-18