Задачи. З.5.1 Опишите условия для струны, упруго закрепленной на обоих концах

З.5.1 Опишите условия для струны, упруго закрепленной на обоих концах.

З.5.2 Выведите дифференциальное уравнение, моделирующее деформации струны, помещенной в упругую среду.

Указание. В функционале энергии (5.2) появится слагаемое 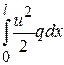, где q(x)dx –- локальный коэффициент упругости среды.

З.5.3 Опишите математическую модель струны, жестко закрепленной в точках x=0 и x=l и подпертой пружиной жесткости k во внутренней точке .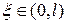

Указание. Мотивируйте появление в функционале энергии (5.2) слагаемого . Заметьте, что наличие в точке 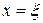пружины влечет за собой потерю гладкости функции u(x) в точке 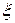(правая и левая производные в точке 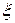различны). Следует разбить интеграл на два – левее и правее точки 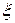. Так как струна в точке 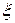не рвется, то здесь естественно появится условие непрерывности, т.е. 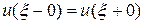. В результате вы должны получить два дифференциальных уравнения (левее и правее 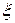) и еще одно условие в точке .

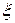З.5.4. Опишите математическую модель упруго-сочлененной в точке 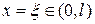(с помощью пружины жесткости k) цепочки из двух струн.

А) Концы цепочки предполагаются жестко закрепленными (в точках x=0 и x=l).

Б) Левый конец цепочки (в точке x=0) упругозакреплен с помощью пружины жесткости 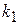,а правый (в точке x= l) свободен.

В) Опишите случай А), если к концам 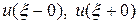струн дополнительно прикреплены пружины жесткост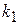и и 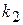соответственно.

Указание. Заметьте, что в данной ситуации функция u(x) терпит разрыв в точке 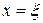. Наличие скрепляющей цепочку в точке 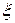пружины ведет к появлению в функционале (5.2) слагаемого 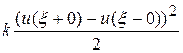. Следует разбить интеграл на два – левее и правее точки .

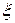§6. Задача Больца.

Так называют задачу исследования на экстремум функционала вида

,

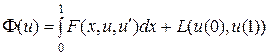где 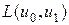- дифференцируемая функция двух переменных, рассматриваемого на множестве 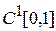. Аналогично простейшей задаче для первой вариации имеем представление

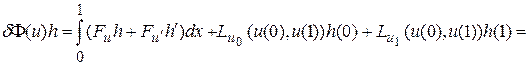
(6.1)

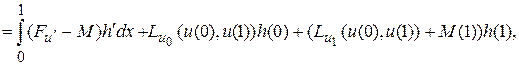
где 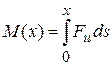. Применяя принцип Ферма, т.е. приравнивая полученное выражение к нулю, воспользуемся произволом в выборе функции h(x), а именно ограничимся лишь функциями h(x) из 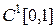, такими, что h(0) = h(1) = 0. На множестве таких функций мы имеем 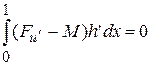, откуда вследствие леммы Дю- Буа- Реймона вытекает, что искомая функция должна удовлетворять равенству

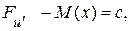(6.2)

продифференцировав которое, получим уравнение Эйлера

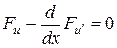. (6.3)

Но тогда выражение (6.1) должно приобрести вид

.

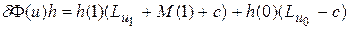Приравнивая его к нулю и пользуясь произвольностью выбора функции h(x), точнее произвольностью чисел h(0), h(1), имеем

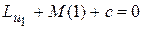(6.4)

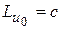(6.5)

С другой стороны, подставим в тождество (6.2) значение x=1 и выразим c. Тогда равенство(6.4) примет вид

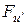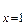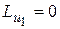| + . (6.6)

Аналогично, если подставить в (6.2) x=0 и выразить константу, то равенство(6.5) примет вид

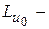
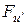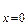| =0. (6.7)

Тем самым мы получили два краевых условия (6.6), (6.7), дополняющих уравнение Эйлера.

§7. Задача Пуассона.

Ставится задача исследования на экстремум функционала

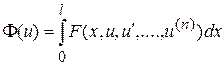, (7.1)

рассматриваемого на множестве G n раз непрерывно дифференцируемых на [0,l] функций, удовлетворяющих равенствам

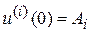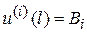, . (i=0,…, n-1) (7.2)

Предполагается достаточная гладкость решения u(x) этойзадачи и функции F:[0,l] 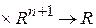. Первая вариация, как легко проверить, имеет вид

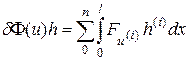(7.3)

при любом h из множества 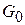n раз непрерывно дифференцируемых на [0,l] функций, удовлетворяющих равенствам

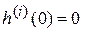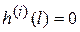, . (i=0,…, n-1) (7.4)

Преобразуя в (7.3) i - ое слагаемое i -кратным интегрированием по частям, имеем

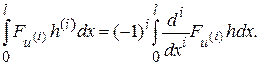
Здесь в силу (7.4) все внеинтегральные слагаемые обращаются в нуль. Подставляя полученное выражение в (7.3) и пользуясь принципом Ферма, имеем

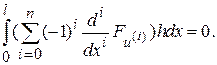(7.5)

Далее нам потребуется следующая

Лемма 7. 1 (Лагранж) Пусть функция A(x) непрерывна на отрезке [0,l], и пусть для любой функции 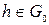выполняется равенство

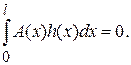
Тогда A(x)=0.

Доказательство. В предположении противного существует точка на отрезке [0,l], в которой 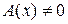. Но тогда, в силу непрерывности A(x), существует и некоторый интервал 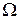, на котором A(x) строго положительна или строго отрицательна. Возьмем в 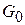функцию 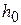, которая строго положительна в 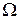и тождественно равна нулю вне 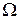. В качестве такой функции можно, например, взять «шапочку». Тогда 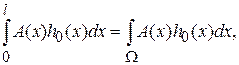причем последний интеграл отличен от нуля, так как его подынтегральное выражение на 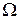нулей не имеет. Лемма доказана.

Применив лемму 7.1. к равенству (7.5), получим

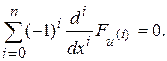(7.6)

Уравнение (7.6) называют уравнением Эйлера – Пуассона.

Дата добавления: 2014-11-18