Упражнения. Простейшие первые интегралы уравнения Эйлера

Простейшие первые интегралы уравнения Эйлера.

Рассмотрим ситуацию, когда функция от не зависит от одной из переменных.

1) 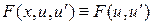. В этом случае множество решений уравнения Эйлера содержится во множестве решений уравнения

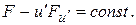(3.13)

В самом деле,

.

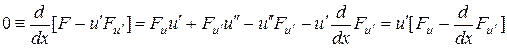Заметим, что уравнение (3.13) может содержать решения вида u=const, вообще говоря, не являющиеся решениями уравнения Эйлера.

2) 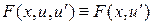. Тогда , и первый интеграл принимает вид .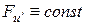

3) . Решение уравнения Эйлера определяется как неявная функция из уравнения 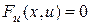, которая, вообще говоря, не удовлетворяет одновременно обоим краевым условиям.

Найдите допустимые экстремали (т.е. решения уравнения Эйлера, удовлетворяющие указанным условиям) для заданных функционалов:

3.1.

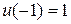
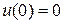
3.2.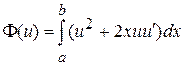

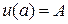
3.3

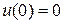
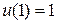
3.4.

3.5.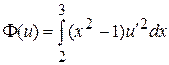

§4. Задача о брахистохроне.

Среди плоских кривых, соединяющих две данные точки, найти ту, двигаясь по которой под действием только силы тяжести, материальная точка соскользнет за кратчайшее время.

Эта древнейшая задача, известная со времен греков, была решена Я.Бернулли, а затем, независимо, Ньютоном и Эйлером в самом конце 17в., явившись первым серьезным приложением новорожденного анализа бесконечно малых. С этой задачи ведет отсчет вариационное исчисление.

Введем систему координат. Пусть в начальный момент времени t = 0 материальная точка имела координаты (0,0); в конечный момент времени t = T - координаты 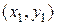(считаем, что 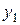> 0, т.е. ось y направлена вниз, а также, что > 0). Пусть искомая кривая есть график функции y = y(x). Тогда при t = 0 y(0) = 0; при t = T , что означает условия закрепления концов

y(0) = 0, . (4.1)

Так как скорость определяется равенством 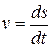, где ds – дифференциал дуги, то 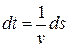. Поэтому время спуска

,

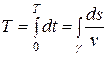где 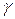– график кривой y = y(x). Мы получили криволинейный интеграл I типа. Так как кривая задана в явном виде, то . Поэтому

.

Выразим скорость через х и y. По закону сохранения энергии 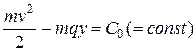, где – кинетическая энергия, -mqy – потенциальная энергия силы тяжести. Так как y(0) = 0, v(0) = 0, то = 0, откуда . Значит, 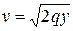. Поэтому

.

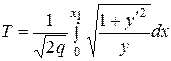Таким образом, задача об отыскании кривой наискорейшего спуска свелась к задаче о минимизации функционала (константа не влияет на поиск точки минимума)

.

Подынтегральная функция не зависит явно от х, поэтому можно воспользоваться следствием уравнения Эйлера – первым интегралом: , т.е.

.

Выражая через y, получим

.

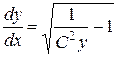Откуда

.

После подстановки , получаем

,

т.е.

.

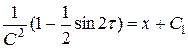Таким образом, кривой наискорейшего спуска является циклоида, уравнение которой в параметрическом виде

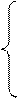
Постоянные С и С могут быть найдены из условий (4.1).

§5. Задача о струне.

Под струной понимается непрерывная нить, упруго реагирующая на растяжение и не реагирующая на изгиб.

Считая струну натянутой вдоль отрезка [0,l], обозначим через u(x) деформацию (смещение) точки x. Подчеркнем, что рассматриваемая функция u(x) – это гипотетическая (виртуальная) деформация. На участке [x, x+dx] приращение длины струны равно , и, по закону Гука, упругая реакция элемента [x, x+dx] пропорциональна растяжению и потому равна 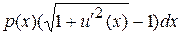. Если прогиб струны вызван лишь внешней силой интенсивности f(x), то на элемент [x, x+dx] действует также сила f(x)dx. Затраченная этой силой работа равна (f(x)dx)u(x) (произведение силы на перемещение). Поэтому энергия, накапливаемая элементом струны длины dx, равна . Значит, если бы струна приняла форму, определяемую функцией u(x), то в целом на [0,l] ее потенциальная энергия равнялась бы

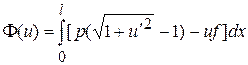. (5.1)

Так как 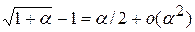, то при вместо в (5.1) с точностью до членов четвертого порядка малости имеем

. (5.2)

В литературе при описании струны деформации обычно предполагаются малыми, и энергия сразу записывается в виде (5.2).

Струна с жестко закрепленными концами. Предположим, что струна жестко закреплена на концах, т.е. точки x=0 и x=l не смещаются. Это означает выполнение условий

u(0)=0, u(l)=0. (5.3)

В силу вариационного принципа (принципа Лагранжа), реальная деформация струны 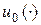решает задачу о минимизации функционала (5.2) при условиях (5.3). Таким образом, мы приходим к простейшей задаче вариационного исчисления при . Уравнение Эйлера в данном случае принимает вид

и из теоремы 3.1. следует, что реальная деформация струны 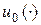должна являться решением задачи

Струна со свободным концом. Предположим, что струна жестко закреплена лишь на левом конце x=0, а правый конец (в точке x=l) с помощью колечка прикреплен к спице, по которой он может вертикально передвигаться (без трения). В силу принципа Лагранжа, реальная деформация струны 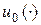решает задачу о минимизации функционала 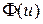при условии u(0)=0.

Воспользуемся схемой, реализованной при выводе уравнения Эйлера. Обозначим через G множество гладких функций u таких, что u(0)=0. Тогда функции вида 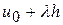, где , , очевидно, принадлежат множеству G. Причем, 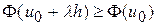. Приравняв производную к нулю, для каждой получаем равенство

(5.4)

Проинтегрировав по частям второе слагаемое (полагая dM=fdx), и подставляя результат в (5.4), будем иметь

(5.5)

Так как равенство (5.5) справедливо для всех , то оно справедливо и для всех 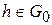, где через 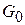мы обозначили множество гладких функций h, удовлетворяющих условиям h(0)=h(l)=0. Но для 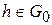равенство (5.5) принимает вид

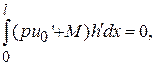
где Воспользовавшись леммой 3.1, получим, что

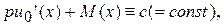(5.6)

что влечет равенство

Подставим теперь полученное тождество (5.6) в (5.5). Получим

т.е.

(5.7)

Равенство (5.7) справедливо для всех , а значит и при .Следовательно, M(l)=c, и тождество (5.6) можно переписать в виде

Так как последнее равенство справедливо в том числе и при x=l, получаем, что

Таким образом, реальная деформация 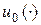струны со свободным правым концом должна являться решением задачи

Важнейший вывод. Имея в исходной задаче только один закрепленный конец, т.е. предопределяя заранее только одно условие, дополнительное к уравнению Эйлера – уравнению второго порядка – мы с неизбежностью получим еще одно условие, причем на другом конце.

Струна с упруго закрепленным концом. Пусть струна жестко закреплена на левом конце (в точке x=0) и подперта пружиной с коэффициентом упругости k на правом (в точке x=l). Наличие пружины ведет к появлению в функционале энергии (5.2) дополнительного слагаемого, порождаемого энергией пружины. Предположим, что длина пружины изменена на величину s (от первоначального положения). Тогда, по закону Гука, при малом изменении s на ds сила сопротивления пружины равна ks. В силу малости ds эта сила может считаться постоянной на промежутке (s, s+ds). Работа, совершаемая этой силой на участке длины ds, будет равна ksds. Значит, смещение правого конца струны на дистанцию u(l) вызовет появление у пружины энергии, адекватной работе суммарно от нуля до u(l), т.е.

Таким образом, функционал потенциальной энергии должен быть записан в виде

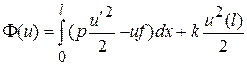. (5.8)

В силу принципа Лагранжа, реальная деформация струны 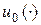решает задачу о минимизации функционала (5.8) при условии u(0)=0.

Первая вариация 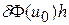функционала должна быть равной нулю, т.е.

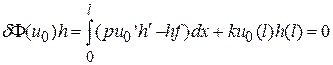(5.9)

для всех h из множества G гладких функций, удовлетворяющих условию h(0)=0.

Проинтегрировав по частям второе слагаемое (dM=fdx), и подставив результат в (5.9), будем иметь

(5.10)

Так как равенство (5.10) справедливо для всех , то оно справедливо и для всех 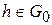, где через 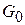мы обозначили множество гладких функций h, удовлетворяющих условиям h(0)=h(l)=0. Но для 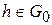равенство (5.10) принимает вид

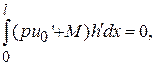
где Воспользовавшись леммой 3.1, получим, что

(5.11)

что влечет равенство

Подставим теперь полученное тождество (5.11) в (5.10). Получим

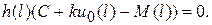(5.12)

Равенство (5.12) справедливо для всех , в том числе и для тех, для которых . Значит, 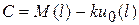, и тождество (5.11) может быть записано в виде

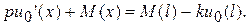
Последнее равенство справедливо в том числе и при x=l, откуда следует, что

.

Мы получили, что реальная деформация 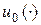струны с упруго закрепленным правым и жестко закрепленным левым концом должна являться решением задачи

Дата добавления: 2014-11-18