Уравнение Эйлера

Среди всех возможных (виртуальных, т.е. теоретически мыслимых) состояний или проявлений реальным для физической системы является то, которое дает минимум полной энергии.

Этот принцип выпал из поля зрения математиков, занимавшихся проблемами математической физики, поскольку он объяснял как бы «в хвост» хорошо уже известные основные типы уравнений математической физики. К сожалению, он вышел из поля зрения дальнейшего развития математики при постановке задач для разного рода упругих систем, где к середине 20 века даже в самых серьезных исследованиях по теории краевых задач (как в [5, 6] и др.) мотивация (обоснование) разнообразных условий трансмиссии, сочленения и даже краевых условий проводилась отсылкой к чисто инженерным работам, авторы которых свои обоснования проводили на языке математики 18 века, даже не подозревая о возможностях в этом плане вариационных методов.

Ниже мы приводим достаточно простую вариационную (в духе Лагранжа) схему обоснования описания разнообразных краевых задач для одномерных континуумов, возникающих в теории упругих систем.

Мы обнаружим, что если опираться на вариационные принципы как на физический постулат, чем они и являются на самом деле, то для континуальных (т.е. с непрерывным пространственным аргументом) объектов помимо дифференциального уравнения обязательно присутствуют дополнительные условия на границе области определения.

В этом параграфе изучается простейшая задача вариационного исчисления, т.е. задача исследования на экстремум функционала

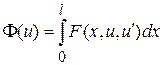, (3.1)

рассматриваемого на множестве G один раз непрерывно дифференцируемых на [0,l] функций, удовлетворяющих условиям закрепления концов

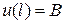, . (3.2)

К задаче вида (3.1)-(3.2) сводятся, например, задача о деформациях струны, натянутой вдоль отрезка [0,l], задача о кривой наискорейшего спуска (задача о брахистохроне), которые будут подробно рассмотрены в последующих параграфах. Мы изложим здесь идеи, играющие ключевую роль в получении дифференциальных уравнений (а также и краевых условий) при математическом моделировании задач математической физики. Эти идеи далее будут нами использованы при изучении различных модификаций задачи о струне, в задаче Больца, задаче Пуассона и в задаче о деформациях стержня.

Здесь и далее применяется сокращенная запись, при которой в корректном виде (3.1) понимается как . При этом у функции трех переменных F, определяемой на , мы сохраним за вторым и третьим аргументом обозначения u и . Чтобы не затенять сути дела, мы будем предполагать, что функция F «достаточно хорошая», т.е. она обладает той степенью регулярности (гладкостью производных), которая нам потребуется в выкладках.

Пусть 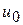дает минимум функционала (3.1), т.е

(случай максимума может быть рассмотрен аналогично). Тогда для всех функций выполняется неравенство

(3.3)

Будем рассматривать функции u(x) специального вида, а именно,

(3.4)

где , а функция h(x) взята из множества 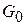– один раз непрерывно дифференцируемых на [0,l] функций, удовлетворяющих условиям

h(0)=h(l)=0.

Очевидно, что всякая функция u, определяемая равенством (3.4), принадлежит множеству G.

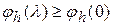Зафиксируем произвольную . Рассмотрим скалярную функцию Из (3.3) следует, что , т.е. значение дает минимум Если при этом функция 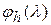окажется дифференцируемой в нуле, то по теореме Ферма, должно быть

(3.5)

Покажем, что производная существует для любой . Имеем

| = | .

Подынтегральное выражение в силу гладкости F равномерно по х, дифференцируемо по . Поэтому и соответствующий интеграл также дифференцируем по , как по параметру, и дифференцирование можно переносить под знак интеграла. Поэтому, применяя известное из математического анализа правило дифференцирования сложной функции, получаем

= . (3.6)

Для сокращения мы опускаем аргументы у рассматриваемых функций, полагая при этом

, .

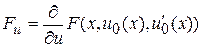Функционал называется первой вариацией в точке 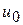и обозначается , т.е. .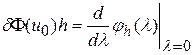

Согласно (3.5), получаем, что для любой

. (3.7)

Преобразуем первое слагаемое в (3.7) интегрированием по частям, полагая

Имеем

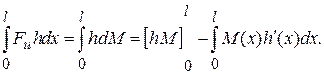
Внеинтегральный член здесь равен нулю в силу условий h(0)=h(l)=0. Подставив полученное выражение в (3.7), получим

() (3.8)

Далее нам потребуется следующая

Лемма 3. 1 (Дю-Буа-Реймон) Пусть функция A(x) непрерывна на отрезке [0,l], и пусть для любой функции 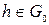выполняется равенство

(3.9)

Тогда A(x) есть константа.

Доказательство. Заметим, что для любой константы и для любой функции h(x) из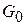

Поэтому условие леммы означает, что

(3.10)

при любом .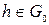

Рассмотрим функцию

Очевидно, , и 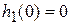. С другой стороны,

т.е. при .

Подставим полученное значение в представление для функции . Теперь, очевидно, . Положив в равенстве (3.10) , , 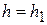получим

,

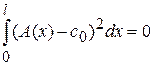откуда . Лемма доказана.

Вернемся к равенству (3.8). Из доказанной леммы следует, что

(3.11)

И потому функция дифференцируема. Продифференцировав равенство (3.11), получим

(3.12)

Уравнение (3.12) называют уравнением Эйлера. Всякое решение уравнения Эйлера называют экстремалью. Экстремали из множества называют допустимыми экстремалями.

Таким образом, нами доказана следующая

Теорема 3.1. Пусть функция F в (3.1) достаточно регулярна. Тогда функция (х), дающая минимум (максимум) при условиях (3.2), является решением уравнения Эйлера (3.12).

Эта теорема сводит поиск оптимальной функции (х) к решению дифференциального уравнения (3.12) при дополнительных условиях (3.2), т.е. к решению двухточечной краевой задачи.

Если раскрыть производную по х в уравнении (3.12) (что возможно, если функция 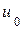дважды непрерывно дифференцируема), то мы получим дифференциальное уравнение второго порядка

.

Дата добавления: 2014-11-18