Методы нахождения обратной матрицы

1) Метод присоединенной матрицы.

Из выше изложенного вытекает следующий алгоритм построения обратной матрицы методом присоединенной матрицы.

1. Вычислить определитель 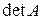. Если 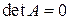, то 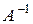не существует.

2. Если 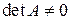, то составляем присоединенную матрицу из алгебраических дополнений соответствующих элементов матрицы A.

3. По формуле (3.2) составляем матрицу .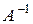

2) Метод с использованием элементарных преобразований матриц.

Матрица записывается в виде 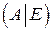, где за вертикальной чертой приписывается единичная матрица того же порядка, как и матрица A. После использования элементарных преобразований получаем матрицу вида 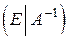, т.е.

.

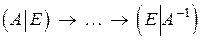Пример 3.3. Найти матрицу, обратную матрице A двумя способами, если

.

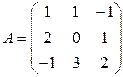Решение. 1) Найдем матрицу, обратную данной, используя метод присоединенной матрицы.

Находим определитель матрицы A.

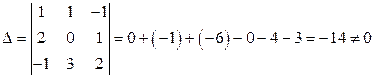
Находим алгебраические дополнения каждого элемента матрицы A.

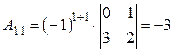
По аналогии находим остальные алгебраические дополнения:

.

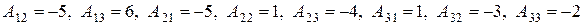Получаем обратную матрицу

.

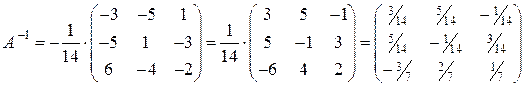2) Найдем матрицу, обратную данной, используя элементарные преобразования матрицы.

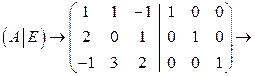
[умножаем первую строку на (-2) и складываем со второй строкой,

складываем первую и третью строки]

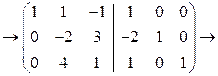
[умножаем вторую строку на (-2) и складываем с третьей строкой]

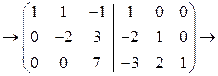
[делим вторую строку на (-2) а третьей строкой - на 7]

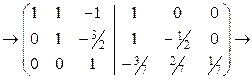
[умножаем третью строку на 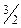и складываем со второй строкой,

складываем третью и первую строки]

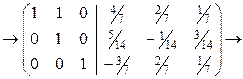
[умножаем вторую строку на (-1) и складываем с первой строкой]

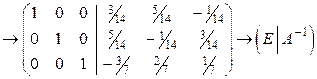
Итак, .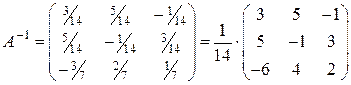

,

4. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

4.1. Основные понятия

Определение 4.1. Системой линейных уравнений (СЛУ), содержащей m уравнений и n неизвестных, называется система вида

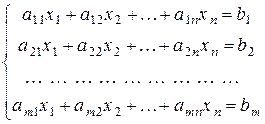, (4.1)

где числа 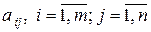называются коэффициентами системы, числа 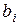- свободными членами.

Коэффициенты обозначаются буквой a с двумя индексами i и j; первый индекс (i) указывает номер уравнения, второй (j) – номер неизвестной, к которой относится данный коэффициент. Число m уравнений может быть больше, равно или меньше числа n неизвестных.

Определение 4.2. СЛУ называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, линейная система называется однородной.

Определение 4.3. Решением СЛУ называется упорядоченная совокупность n чисел:

,

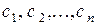подстановка которых вместо 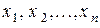соответственно 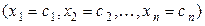обращает в тождество каждое из уравнений этой системы.

Всякое решение системы можно записать в виде матрицы-столбца

.

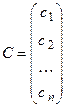Допускается и такая запись: 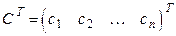или .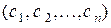

Определение 4.4. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Отметим, что однородная система всегда совместна, так как она имеет нулевое решение 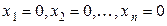, которое называется нулевым или тривиальным.

Определение 4.5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Решить СЛУ – это значит выяснить, совместна она или несовместна. Если система совместна, найти все ее решения.

Определение 4.6. Две системы называются эквивалентными (равносильными), если любое решение одной из них является также решением другой и обратно, т.е. если они имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.

Элементарными преобразованиями линейной системы называются следующие преобразования: 1) перестановка местами двух уравнений системы; 2) умножение уравнения системы на число, отличное от нуля; 3) прибавление к одному уравнению системы другого ее уравнения, умноженного на любое число, отличное от нуля.

Линейную систему можно записать в матричной форме.

Рассмотрим СЛУ (4.1).

Матрица, составленная из коэффициентов линейных уравнений системы

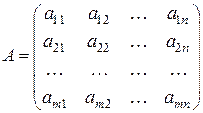
называется основной матрицей системы.

Матрица, полученная из основной присоединением столбца из свободных членов

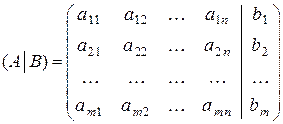
называется расширенной матрицей системы.

Матрицы-столбцы, составленные из неизвестных и свободных членов имеют вид:

, .

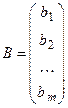Поскольку матрица A согласована с матрицей X, то можно найти произведение

.

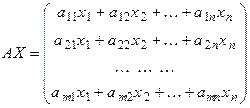Элементы этой матрицы-столбца являются левые части уравнения системы (4.1), поэтому на основании определения равенства матриц

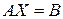(4.2)

Таким образом, СЛУ (4.1.) можно записать в идее одного матричного уравнения (4.2.), которое называется матричной формой.

Дата добавления: 2014-11-18