Тема 1.1. Матрицы и определители. Системы линейных алгебраических уравнений (СЛАУ)

Ряды. Преобразование Фурье (42 часа)

Кратные интегралы (38 часов)

Криволинейные интегралы (6 часов)

Обыкновенные дифференциальные уравнения и системы

Интегральное исчисление функций одной переменной

(40 часов)

6.1. Первообразная. Неопределенный интеграл. Основные свойства неоп­ределенного интеграла. Таблица интегралов. Интегрирование по час­тям и методом замены переменной.

6.2. Интегрирование рациональных дробей, простейших тригонометриче­ских выражений, линейных и дробно-линейных иррациональностей.
Квадратичные иррациональности.

6.3. Определенный интеграл, его свойства и методы вычислений. Несобст­венные интегралы. Приложения определенных интегралов в геометрии
и механике.

(44 часа)

7.1. Физические задачи, приводящие к дифференциальным уравнениям.
Основные понятия теории дифференциальных уравнений.

7.2. Дифференциальные уравнения первого порядка: с разделяющимися
переменными, однородные и приводящиеся к однородным, линейные
уравнения, уравнения в полных дифференциалах.

7.3. Задача Коши. Теорема существования и единственности решения зада­чи Коши. Понятие особого решения дифференциального уравнения.
Огибающая семейства кривых.

7.4. Дифференциальные уравнения высших порядков. Задача Коши. Поня­тие о краевых задачах для дифференциальных уравнений. Теорема су­ществования и единственности решения задачи Коши. Понятие общего
и частного решений.

7.5. Уравнения, допускающие понижение порядка. Линейные дифференци­альные уравнения высших порядков. Линейно-зависимые и линейно-
независимые системы функций. Определитель Вронского, его свойст­ва.

7.6. Линейные однородные дифференциальные уравнения с постоянными
коэффициентами, линейная независимость их решений, фундаменталь­ная система решений.

7.7. Линейные неоднородные дифференциальные уравнения с постоянны­ми коэффициентами. Структура общего решения. Метод Лагранжа ва­риации произвольных постоянных. Линейные неоднородные диффе­ренциальные уравнения с постоянными коэффициентами со специаль­ной правой частью.

7.8. Системы дифференциальных уравнений. Нормальные системы. Реше­ние нормальной системы методом исключения. Задача Коши для нор­мальных систем.

7.9. Элементы теории устойчивости.

8.1. Криволинейные интегралы первого рода, вычисление.

8.2. Криволинейные интегралы второго рода, вычисление, приложения. Не­зависимость криволинейного интеграла от формы пути интегрирова­ния, криволинейный интеграл от полного дифференциала, восстанов­ление функции по полному дифференциалу.

9.1. Двойной интеграл, условия существования и свойства. Вычисление
двойного интеграла в декартовой и полярной системах координат.

9.2. Тройной интеграл, его свойства. Вычисление тройного интеграла в де­картовой, цилиндрической и сферической системах координат. Прило­жение кратных интегралов к решению геометрических, механических и
физических задач.

9.3. Поверхностные интегралы первого и второго рода, вычисление. Фор­мулы Гаусса - Остроградского, Стокса.

9.4. Скалярное поле и его характеристики. Векторное поле. Векторные ли­нии и трубки, их дифференциальные уравнения. Поток векторного по­ля через открытую и замкнутую поверхность, его свойства, вычисле­ние.

9.5. Дивергенция векторного поля, физический смысл, свойства, вычисле­ние. Теорема Остроградского.

9.6. Ротор векторного поля. Физический смысл, свойства, вычисление. Ли­нейный интеграл, циркуляция вектора поля по контуру, вычисление.
Теорема Стокса.

9.7. Векторные дифференциальные операции первого и второго порядков.
Оператор "набла", свойства, действия с оператором. Основные типы
векторных полей: соленоидальное, потенциальное, гармоническое, их
характеристики. Потенциал векторного поля, его вычисление. Основ­ная теорема векторного анализа.

10.1. Числовые ряды. Сходимость и сумма ряда. Геометрическая прогрессия.
Необходимое условие сходимости ряда. Простейшие действия над ря­дами. Ряды с положительными членами.

10.2. Теоремы сравнения. Признаки сходимости Даламбера, Коши. Инте­гральный признак сходимости ряда.

10.3. Оценка остатка ряда с помощью интегрального признака. Знакочере­дующиеся ряды. Теорема Лейбница, оценка остатка ряда. Знакопере­менные ряды. Абсолютно и условно сходящиеся ряды. Теорема о схо­димости абсолютно сходящегося ряда. Ряды с комплексными членами.

10.4. Функциональные ряды, область сходимости. Равномерная сходимость.
Признак Вейерштрасса.

10.5. Степенные ряды. Теорема Абеля. Круг сходимости, интервал и радиус
сходимости для рядов с действительными членами. Теорема о равно­мерной сходимости степенного ряда. Непрерывность суммы. Интегри­рование и дифференцирование степенных рядов.

10.6. Ряд Тейлора. Теорема о единственности разложения функции в ряд
Тейлора. Применение степенных рядов к решению дифференциальных
уравнений. Приближенные вычисления.

10.7. Ряд Фурье. Коэффициенты Фурье. Приближение в среднем. Свойства
минимальности коэффициентов Фурье. Теорема о сходимости в сред­нем и поточечной сходимости тригонометрических рядов Фурье.

10.8. Понятие ортонормированной системы функций, заданных на интервале
(‑p, p ). Разложение в тригонометрический ряд Фурье функций, задан­ных на интервале (a, b). Интеграл Фурье. Комплексная форма интегра­ла и ряда Фурье. Преобразование Фурье. Синус- и косинус-
преобразования Фурье. Свойства преобразования Фурье.

Раздел 1. Матрицы и определители. Векторная алгебра. Аналитическая геометрия. Элементы линейной алгебры

Учебники: [1, гл. 5, §§ 1 - 6], [10, дополнение к гл. 1], [16, гл. 6, 11, § 1 ]. Аудиторная работа: [ 2, №№ 14.4 (6), 14.7 (2), 14.21 (9), 15.2 (3), 15.5 (1-

3, 9), 15.45 (1,2), 15.65 (1), 16.18 (1, 4, 12, 20), 17.2 (1, 3), 19.1 (3, 9)], [ 7, гл. 2,
§§ 1-3, №№ 1, 2 (1, 3), 3 (1, 3), 5, 19 (1, 2, 4), 20 (1, 2), 22 (13), 24 (3, 7), 25 (1,
4), 29 (1)], [ 18, №№ 5, 11, 23, 55, 75, 82, 257, 260, 608, 609, 689, 700, 725], [20,

4, 1, гл. 3, § 1-4, №№ 3.1, 3.8, 3.12, 3.55, 3.78, 3.80, 3.91, 3.106, 3.114, 3.121,
3.150, 3.187, 3.192, 3.198, 3.207, 3.210], [28, занятия 1 (1.2.1, 1.2.3, 1.2.9,
1.2.15), 2(2.2.2.-2.2.4), 10(10.2.1., 10.2.4(6 - д), 10.2.5, 10.2.7), 11 (11.2.1 (а, б,
в), 11.2.2 (а, б), 11.2.3 (а, б), 11.2.4), 12 (12.2.1 (а, б, в, г), 12.2.2, 12.2.4, 12.2.5
(в), 12.2.7 (в))].

Самостоятельная работа: [ 2, №№ 14.7 (3, 4), 14.21 (11, 12), 15.5 (7,9,13), 15.45 (4, 7), 15.65 (2, 4), 16.18 (6, 12, 20, 21), 17.2 (2, 4, 5), 19.1 (2, 3,

5, 8, 10)], [ 7, гл. 2, §§ 1-3, №№ 2 (2, 4), 3 (2, 4), 19 (3, 5, 6, 8), 20 (3, 4), 22 (3,
4), 24 (4, 5, 7, 8), 25 (3, 5), 29 (2)], [18, №№ 6, 11, 17, 25, 43, 44, 83, 84, 116,
118, 258 - 260, 270, 554, 690, 691, 698, 726, 727, 729], [20, ч. 1, гл. 3, §§ 1-4,
№№ 3.2, 3.13, 3.56, 3.57, 3.79, 3.91, 3.85, 3.92, 3.110, 3.119, 3.124, 3.151, 3.152,
3.208, 3.211, 3.215], [ 28, задания 1, 2 (2.3.1-2.3.5), 10, 11, 12].

Прямоугольной матрицей называется совокупность m • n чисел, распо­ложенных в таблице из m строк и n столбцов.

.

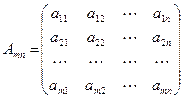Числа 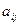, , 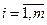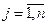входящие в данную таблицу, называются
матричными элементами, а индексы i и j элемента 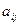указывают (соответст­венно) номера строки и столбца, в которых расположен элемент.

Если m = n, то матрица называется квадратной. Квадратная матрица из n строк и n столбцов называется матрицей n -го порядка. Каждой матрице по­рядка n ставится в соответствие число, которое называется определителем, или детерминантом этой матрицы и обозначается одним из следующих сим­волов:

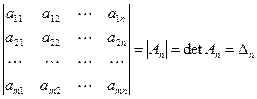. (1.1.1)

Числа называются элементами определителя.

Если определитель матрицы равен 0, то матрица называется особенной (вырожденной), а если определитель отличен от 0 - неособенной (невырож­денной).

Квадратная матрица называется симметрической, если , т. е. рав­ны элементы, симметричные относительно главной диагонали (главная диа­гональ образована элементами .

Диагональной называется матрица, у которой все элементы, не принад­лежащие главной диагонали, равны 0.

Единичная матрица - это диагональная матрица, у которой все элемен­ты главной диагонали равны 1. Обозначается единичная матрица буквами Е
или I.

Дата добавления: 2014-11-20